最优二叉搜索树问题

给定关键字的BST数目

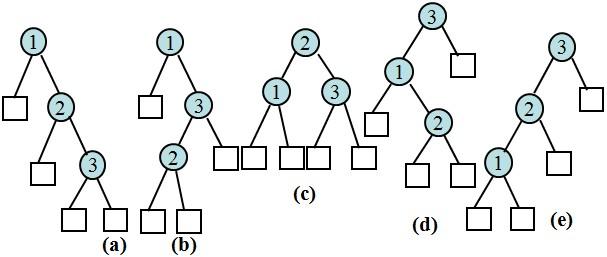
设\(L\)为包含\(n\)个关键字的元素互异的递增序列，把\(L\)可形成的所有形态的BST数目计为\(C(n)\)，然后推导\(C(n)\)的递推表达式，其核心在于按\(L\)每个元素作树根的情况划分问题，然后得出\(C(n)\)与每个根节点左右子树的\(C\)的关系并求和：第1个关键字为树根时有\(C(n-1)\)种情况，第2个关键字为树根时有\(C(n-2)\)种情况…第5个时有\(C(4)C(n-5)\)种…第k个时有\(C(k-1)C(n-k)\)种…。整理得到\(C(0) = 1\)，\(C(n+1) = \sum_{i=0}^n C(i)C(n-i)\)。\(C(n)\)被称为Catalan数，其以比利时数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名，是组合数学与计算机科学中的重要概念。

 

给定关键字的最优BST

\(
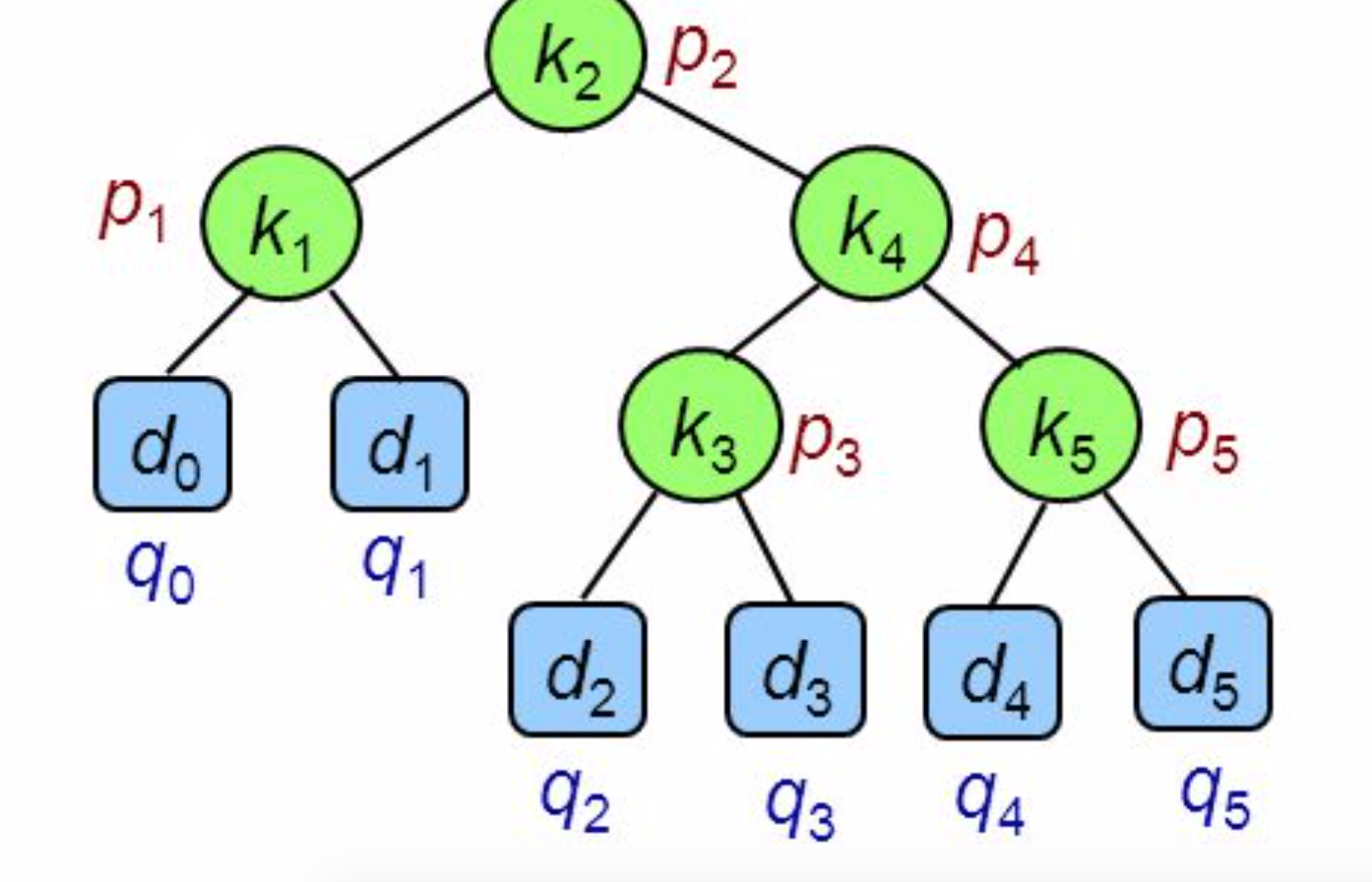
w(i,j)=\sum p + \sum q= w(i,r-1) + p_r + w(r+1,j) = w(i,j-1) + p_j + q_j
\)

 

\(
e(i,j)=
\begin{cases}
q_{i-1} & j-i=-1 \\ \\
w(i,j) + min\{ e(i,r-1) + e(r+1,j) ~|~ i \leq r \leq j \} & j-i > -1
\end{cases}
\)

 

给定含\(n\)个互异元素的递增序列\(K=[k_1,k_2,…,k_n]\)。以及\(n+1\)个元素的序列\(D=[d_0,d_1,…,d_n]\)，其中\(d_0\)表示小于\(k_1\)的“情况”，\(d_i\)表示小于\(k_{i+1}\)大于\(k_i\)的“情况”。若把\(K\)建成BST并执行BST搜索，结果必属于\(K,D\)。然后给定\(K,D\)的搜索频率序列\(P,Q\)。若把\(K\)建成BST并按\(P,Q\)中记录的各关键字或“情况”的搜索频率执行大量BST搜索运算，其中使搜索的期望时间最短的形态的BST被定义为最优BST。接下来用DP策略解出最优BST。

首先应当把期望时间理解为从BST根节点到达各种关键字或“情况”的期望路径长度，即所有关键字的层数*频率的总和。为了统一处理\(K,D\)可以把\(D\)当成BST叶节点计算层数，因为实际搜索失败时确实等价于向下多搜索一次。该问题的最优子结构较简单：“最优BST的左右子树必为最优BST”。选择根节点的方式与之前的矩阵连乘相似，需要通过枚举最小状态来选择。给出状态转移方程如上所示，其中辅助函数\(w(i,j)\)表示\(k_i\)到\(k_j\)所有搜索成功或失败的频率和，\(e(i,j)\)为\(k_i\)到\(k_j\)所能形成的最优BST的期望路径长度。这里处理\(w,e\)的关系时用到了个小技巧就是在每个子树都把所有子节点的频率累加，最终递归的得到所有关键字的层数*频率的总和。在编程自底向上递推时，递推顺序也要使用类似于之前矩阵连乘中的策略保证每次计算都是正确的，并且额外维护“备忘录”数组\(root(i,j)\)记录\(k_i\)到\(k_j\)的根节点下标。该问题的边界处理较麻烦，需要注意到在输入输出时\(K,P\)的开始下标为1，\(D,Q\)的开始下标为0。