最长公共子序列问题
F(i,j)=
\begin{cases}
1 & ij=0,~X_i = Y_j \\
0 & ij=0,~X_i \neq Y_j \\
F(i-1,j-1)+1 & ij>0,~X_i = Y_j \\
max[~F(i-1,j),F(i,j-1)~] & ij>0, ~ X_i \neq Y_j \\
\end{cases}
\)
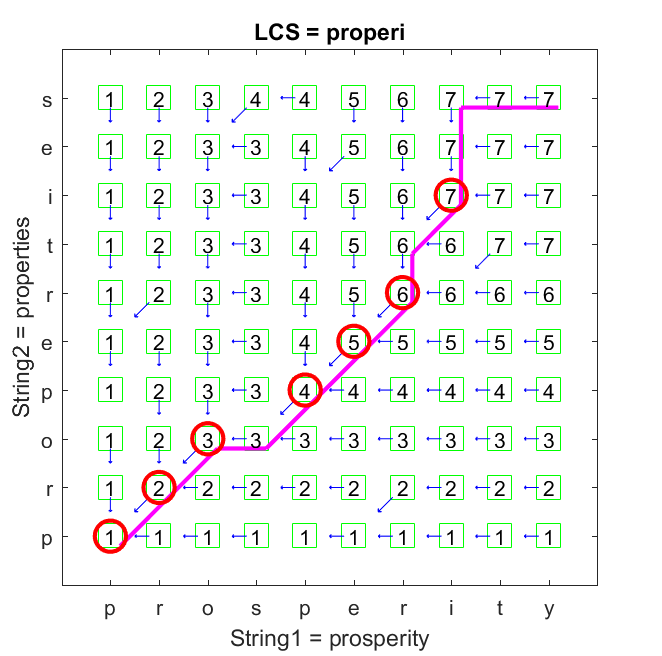
最长公共子序列(LCS)问题中LCS的定义为“对于任意两个序列\(X,Y\),若\(Z\)为其LCS,则\(Z\)中的所有元素必然同时存在于\(X,Y\)中,且其在\(X,Y\)中的下标是递增的”。首先定义状态转移函数\(F(i,j)\)表示原问题中\(X[0…i],Y[0…j]\)子序列的LCS长度,容易得出状态转移方程如上,因为\(F(i,j)\)是单调递增的。如上图所示,在递推\(F(i,j)\)状态的同时,如果维护一个“备忘录”数组,则可利用其求出其中一个LCS,并且注意到对\(F(i-1,j)=F(i,j-1)\)的情况加以处理可求出全部LCS。下文的代码仅通过回溯状态转移数组求出其中一个LCS。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | def dp(X,Y): f = [ [ 0 for j in Y ] for i in X ] for i in range(len(f)): for j in range(len(f[i])): if i*j == 0: f[i][j] = 1 if X[i]==Y[j] else 0 else: f[i][j] = 1 + f[i-1][j-1] if X[i]==Y[j] else max(f[i-1][j],f[i][j-1]) return f def lcs(X,Y): f = dp(X,Y) i = len(X) - 1 j = len(Y) - 1 s = [] while i>0 and j>0: if X[i] == Y[j]: i -= 1 j -= 1 s.append(X[i]) elif f[i-1][j] > f[i][j-1]: i -= 1 else: j -= 1 if i == 0 and X[0] in Y[:j+1]: s.append(X[0]) elif j == 0 and Y[0] in X[:i+1]: s.append(Y[0]) s.reverse() return ''.join(s) |