斐波那契堆

斐波那契堆(Fibonacci Heap)

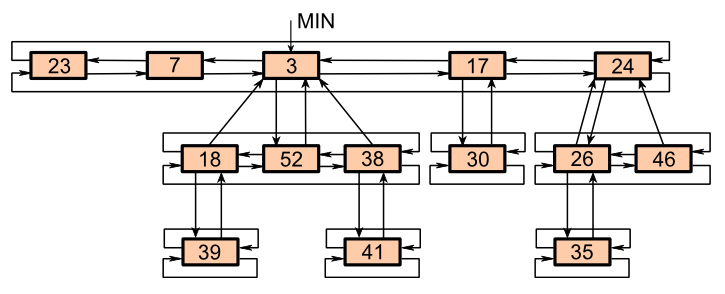
F堆可以认为是“松散”版的二项堆，其也是基于“链表+树”的。F堆上的树无需是二项树，其仅松散的要求链表上的树根出度唯一(仅要求某些运算结构维护该性质)。并且注意到F堆使用“双向循环链表”的物理结构表示链表与树，这种链表不承载序信息，故F堆的链表与树都是无序的。相比二项堆用“孩子兄弟法”表示树，F堆在用“双向循环链表”表示树时，需把所有子节点都指向父节点，而父节点只需一个指向其任意子节点的指针。最后明确“双向循环链表”只有单节点时，该节点的左右指针都指向其自身。F堆用最小节点指针\(min\)实现二项堆的链表表头指针\(head\)的作用。

F堆的运算与二项堆相同，其除\(pop\)与\(delete\)的代价为\(O(lgn)\)，其他运算的代价为\(O(1)\)。所以F堆的理论代价非常的优秀，但由于其实际代价中隐含着“大系数”，故程序语言中的优先队列不用F堆，F堆只适用于需要大量执行其\(O(1)\)运算的场景(如MST/Dijkstra)，所以通常认为F堆只是一个理论上更高效的结构。

为在之后分析时间复杂度，定义\(D(n)\)为任意\(n\)节点F堆的所有节点的出度上界值，\(t(H)\)为F堆\(H\)的链表节点数。根链表节点出度唯一性被满足时\(t(H) \leq D(n(H)) + 1\)，因为该条件下出度取值最坏情况为\([0,1,…,D(n(H))]\)，故链表节点数目的最坏情况为\(D(n(H)) + 1\)。给出F堆几种代价为\(O(1)\)的简单运算的具体实现：

\(push\)：将关键字(节点)插入根链表任意位置，最后更新\(min\)即可；

\(union\)：按任意次序合并两个链表，最后更新\(min\)即可；

\(minimum\)：直接返回\(min\)指针即可；

出堆运算

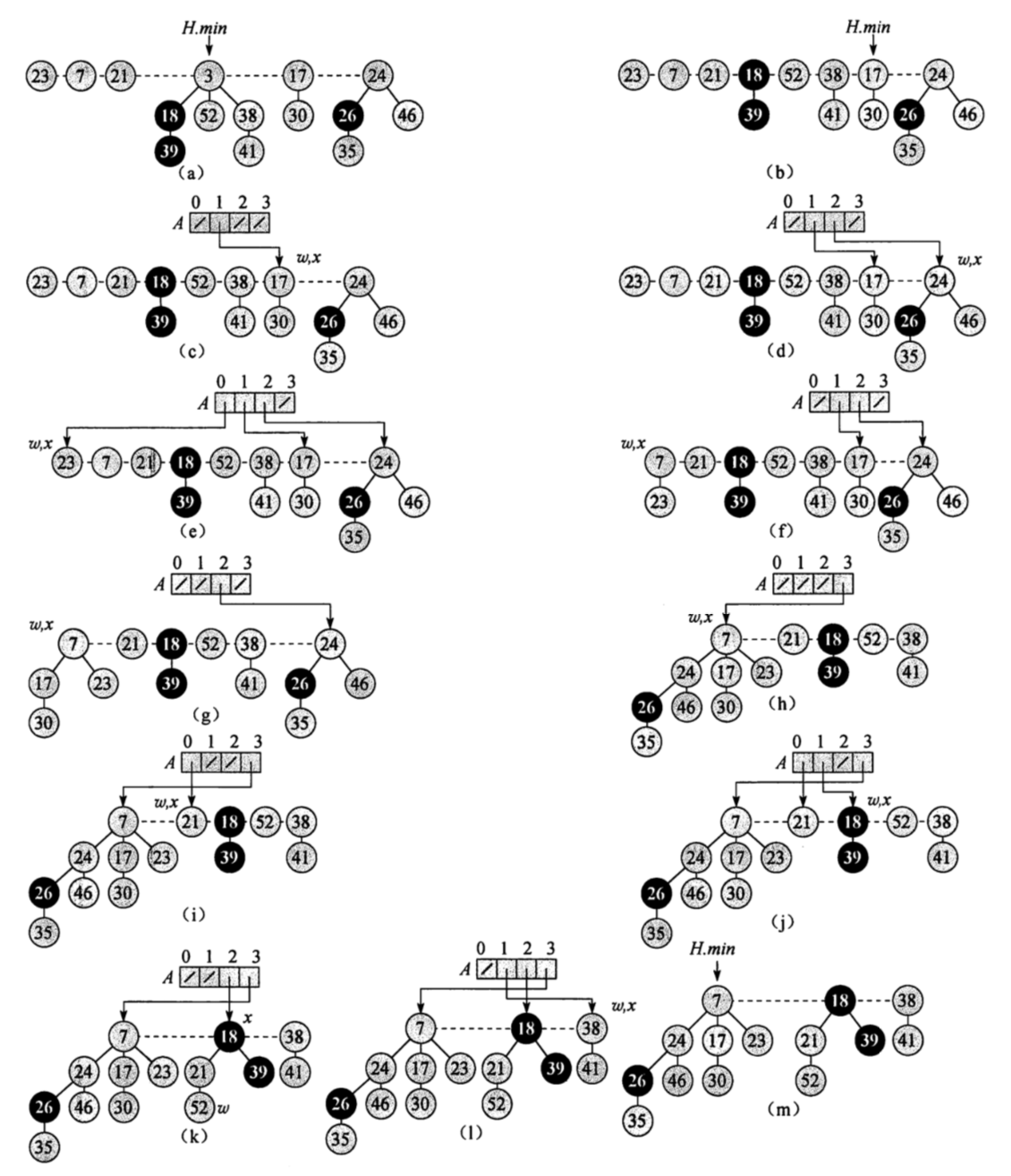
1) 通过\(min\)找到最小节点将其移出根链表，但把其全部子节点任意的合并到根链表，该步骤类似于二项堆的出堆运算。最后把\(min\)指向任意其他根链表节点(\(min\)的性质会在最后被恢复)；

2) 循环的合并根链表出度相等的树根，直到根链表所有树根出度唯一。循环开始前定义临时Map为\(A[i] = N\)，其中\(i\)为出度，\(N\)为根链表中当前“已检查到”的出度为\(i\)的树根。然后执行嵌套循环如下，循环结束后所有树根出度唯一：

2.1) 外层循环为遍历根链表。每轮循环后已遍历过的树根(包括合并后的新树根)的出度是唯一的；

2.2) 内层循环为合并相同出度的已遍历过的树根。其具体流程为先得出当前树根的出度\(x\)，然后检查\(A[x]\)中是否有节点，如果没有则此时已遍历过的树根的出度都是唯一的，最后更新\(A[x]\)并退出内层循环。否则将两个树根合并为新树根，删除\(A[x]\)的记录，然后继续循环的检查\(A[x+1]\)中是否有节点……

注意到步骤(1)结束后，新链表有至多\(O(t(H)+D(n))\)个节点，步骤(2)至多有\(O(t(H)+D(n))\)次合并，无论外循环如何，内层循环有总次数上界\(O(t(H)+D(n))\)，这是个实际代价上界。循环结束后根链表节点出度无重复，结合上文公式可进一步得上界\(O(2D(n)+1)=O(D(n))\)。

减值运算

减值是把\(H\)指定节点的关键字更新为更小值的运算，利用减值运算可进一步构造与二项堆删除运算逻辑相同的F堆删除运算。首先为节点引入\(mark\)布尔变量，当节点上次成为子节点后失去过孩子则\(mark\)为真，否则\(mark\)都为假，节点初始化时\(mark\)为假。下面讨论减值运算\(decrease(node,key)\)：

1) 若\(node.key < key\)则引发异常，否则设定\(node.key=key\)；

2) 若\(key < parent.key \)，则\(parent\)违反小根堆性质。需把\(node\)子树从\(parent\)“切割”并加入根链表，这样两个树的小根堆性质得以满足。然后维护新的\(node\)树的\(parent\)为空\(mark\)为假，\(parent\)在该步骤仅令其出度减1；

3) 若\(parent\)为根节点则仅需维护出度等变量并退出。否则若\(parent.mark\)为假则将其标记为真，然后维护其他变量并退出。若\(parent.mark\)为真，则需对\(parent\)执行“切割”，并继续递归的对\(parent.parent\)执行步骤(3);

设\(m(H)\)为\(H\)中\(mark\)为真的节点总数，势能\(\Phi(H) = t(H) + 2m(H) \)，\(c\)为上述运算的“切割”次数。则实际代价为\(O(c)\)，运算后链表节点数为\(t(H) + c\)，\(mark\)节点数为\(m(H)-c+O(1)\)。故运算前后势差为\(-c+O(1) \)，摊还代价为\(O(c)-c\)。为势能配正常数\(\Phi’ = A\Phi + B\)，其同样满足\(\Phi'(H_0) = 0\)与\(\Phi’ \geq 0\)，新的摊还代价为\(O(c)-Ac\)。如果选定的\(A\)能大过实际代价中的隐藏常数，则摊还代价\(O(c)-Ac\)可合并为\(-O(c)\)，又由于每次该运算的摊还代价不能小于实际代价，故\(-O(c)\)不能取到这个负号，所以摊还代价为\(O(1)\)。

论证\(D(n) = O(lgn)\)

考虑证明\(D(n) \leq log_{\phi} n\)来证明原命题，其中\(\phi = \frac{1+\sqrt{5}}{2}\)是黄金分割比。该证明的过程蕴涵了“斐波那契堆”这个名字的来历。另外注意本文中的斐波那契数列\(F\)，规定其首元素下标为0，并且\(F_0=0\)。

引理1：设\(x\)为任意F堆的任意节点，\(k\)为\(x\)的出度。在任意运算结束后，将\(x\)的所有下一代节点按被“链入”\(x\)的次序排序为\(y_1,…,y_k\)。那么不等式关系\(y_1.degree \geq 0\)与\(y_i.degree \geq i -2 \)成立。

仅考虑仅在出堆时发生的“链入”，对\(y_i\)(\(i>1\))因为\(y_1,…y_{i-1}\)仅在之前被链入，且链入在两树出度相等时发生，故\(y_i.degree = i-1\)。

若合并考虑\(x\)的下一代发生过“切割”，则\(y_i.degree \geq i-1\)。

再进一步合并考虑\(y_i\)在成为\(x\)的下一代后\(y_i\)的下一代发生过“切割”的情况，根据“减值运算”步骤，\(y_i\)在被“链入”\(x\)作为\(x\)的子节点的前提下，\(y_i\)只有一次子节点被“切割”的机会。综上得出\(y_i.degree \geq i-2\)。

引理2：对任意整数\(k \geq 0\)，斐波那契数列\(F\)满足\(F_{k+2} = 1 + \sum_{i=0}^k F_i\)。

该结论可通过数学归纳法证明，其可被看作是斐波那契数的另一种定义。

\(k=0\)时\(F_2 = 1 + F_0 = 1 + 0\)，故原式成立。

\(F_{k+2} = F_{k} + F_{k+1} = F_{k} + (1+\sum_{i=0}^{k-1} F_i) = 1+\sum_{i=0}^{k} F_i\)，

上式说明若\(k+1\)时原式成立，那么在\(k+2\)时原式也必然成立。至此通过数学归纳法证明了原命题。

引理3：对任意整数\(k \geq 0\)，斐波那契数列\(F\)满足\(F_{k+2} \geq \phi^k\)。

从\(F_2 \geq \phi^0, F_3 \geq \phi^1\)数学归纳，因为\(F_{k+2} = F_{k+1} + F_k\)，故\(F_{k+2} \geq \phi^{k-1} + \phi^{k-2}=\phi^{k-2}(\phi+1) \)，

根据黄金分割比的定义\(\phi\)为\(x^2 = x+1\)的解，故\(\phi^{k-2}(\phi+1)=\phi^k \)，综上有\(F_{k+2} \geq \phi^k \)。

引理4：设\(x\)为任意F堆的任意节点，\(k\)为\(x\)的出度，\(size(x)\)为\(x\)子树的节点总数。则\(size(x) \geq F_{k+2} \geq \phi^k\)。

设\(s_k\)为任意F堆任意出度为\(k\)的节点的最小可能\(size\)(\(s_0=1,s_1=2…\))，\(s_k\)显然严格单调递增。

然后根据引理1有\(s_k \geq 1+1+\sum_{i=2}^k s_{y_{i}.degree} \geq 2+\sum_{i=2}^k s_{i-2}\)。

然后用数学归纳法证明\(s_k \geq F_{k+2}\)，\(k\in \{0,1\}\)时原命题成立，

归纳步\(s_k \geq 2+\sum_{i=2}^k s_{i-2} \geq 2+\sum_{i=2}^k F_i = 1+\sum_{i=0}^k F_i = F_{k+2} \)，结合其他引理原命题得证。

最后利用上述引理证明任意n节点F堆\(H\)所有节点的出度上界为\(O(lgn)\)。设\(x\)为\(H\)的任意节点，则\(n \geq size(x)\)。然后设\(x\)的出度为\(k\)，利用引理4有\(n \geq size(x) \geq  \phi^k\)，解得\(k \leq log_{\phi}n\)，原命题证毕。

具体实现

实现时需要谨慎处理好斐波那契堆的双向循环链表的物理结构，具体Python代码如下：