直接寻址表(Direct Address Table)
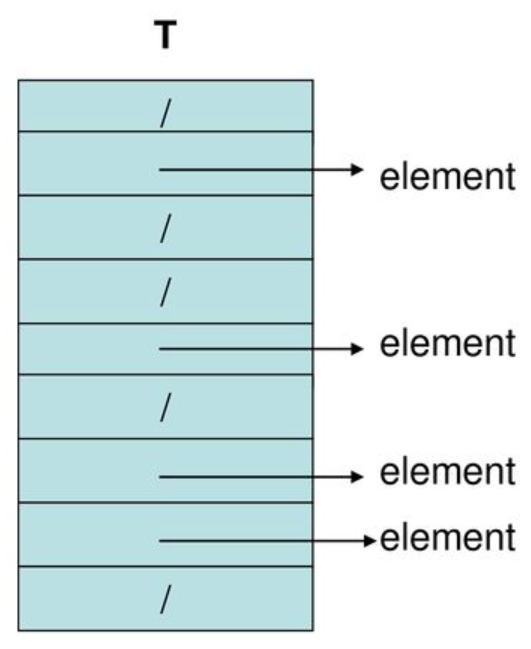
数组是把所有元素按顺序存储在连续内存地址中的，如果单个元素需要的内存地址数越多，数组整体需要的内存地址数就要成倍增长。显然同样大小的连续内存比不连续内存更“稀缺”，因为即使有足够的内存，也不代表有足够的连续内存。那么为更合理的使用内存，在元素数量多且单个元素很大的场景下就不应直接使用大数组存储，而是应该考虑使用链表，但如果对按索引访问的性能有高的要求，就需要结合数组和链表的特点构造一种新的称为直接寻址表的结构。直接寻址表本身是个数组，但元素不存入数组，而是存入不连续的其他内存区域，数组中存储的是元素的内存地址。
直接寻址表的各个位置称为槽(slot)，其允许索引不连续(索引1有元素、索引2没元素、索引3又有元素……)，所以把索引改称为关键字(key)。当元素不大时，也允许不存地址，而是依然存元素本身。所以数组可看作直接寻址表的特例，很多时候甚至不区分这两个概念，因为直接寻址表仅多了1次按地址找元素的步骤，和数组的代价是没有区别的。直接寻址表还有些其他好处，数组创建时必须确定每个元素占用的固定大小。直接寻址表就自由的多，由于其存储的只是地址，所以元素的大小可以不同。事实上很多程序语言中“基于数组”的数据类型更接近直接寻址表而不是数组，比如Python的list。
哈希表(Hash Table)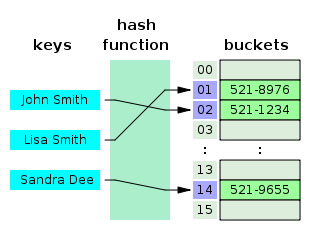
把直接寻址表(数组)看作表示“关键字(索引)到元素的映射”的结构时，会发现这种关键字存在局限性：
1) 只能用自然数作关键字，关键字的表达能力受限；
2) 把关键字用作非索引用途(比如用来表示年份、人数等)，可能有巨大的空间浪费。比如要用直接寻址表记录“2001~2005年每年的人口总量”，那就要创建有2006个槽的直接寻址表，但表里只有5个元素，0~2000的槽都空着；
其原因是数组索引本来只是描述前驱后继关系的，且容易换算为内存地址。这种局限性可通过引入哈希函数解决，哈希函数是“关键字集合”到“\([0,1,…,m-1]\)”的映射(广义的哈希函数可以是任何函数)，进而就能实现“关键字集合”到“直接寻址表各槽位”的映射，比如把2001~2005映射到某个直接寻址表的0~4槽，比如把”John”和”Johnny”都映射到0槽、把”Tom”和”Tommy”都映射到1槽等等。具有哈希函数的直接寻址表就是哈希表，直接寻址表可看作哈希表的特例。通常从程序开始到结束，只有部分关键字被使用过，所以一般把哈希函数设计为值域小于定义域的，但这会导致多个关键字映射到同个槽位，这称为哈希冲突(哈希碰撞)。之后具体讨论哈希函数的选择和处理哈希冲突的方法。
哈希函数
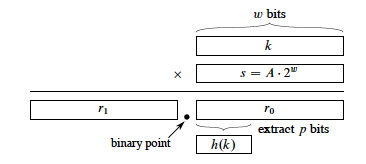优秀的哈希函数应当是满足如下条件的：
1) 简单性：计算简单能有\(O(1)\)的程序实现，哈希函数背后是直接寻址表，应保持直接寻址表的性能；
2) 均匀性：把所有关键字进行哈希后，各槽位的关键字数应尽量的相等；
3) 随机性：相似关键字的哈希值不相似，一般的场景并不非常强调这一点；
考虑到非自然数关键字时，一般是先将其转换为自然数，比如对于英文字符串，其每个字符都对应0~127的ASCII码，那干脆把字符串从左到右当成128进制数，其中每个位是每个字符的ASCII码，这能保证每个字符串都对应唯一自然数，这也是种字符串的惯用处理方法。转换完后就可根据“非自然数关键字对应的自然数的分布”、“自然数关键字的自然数的分布”设计关于自然数的哈希函数。之后讨论的哈希函数默认定义域是自然数或自然数的子集。这里看几种常用哈希函数：
1) 除法哈希函数：取关键字对\(m\)的余数为哈希值。\(m\)的选择不是任意的，比如\(m = 2^p\)等效于取二进制数的低\(p\)位，那么低\(p\)位相同的二进制数会有相同的哈希值，尤其是对字符串关键字的哈希值(假设字符串会按前面的方法转换为自然数)。考虑到各种情况，通常不太接近2的幂的素数是一个较好的选择；
2) 乘法哈希函数：用关键字\(k\)乘常数\(A(0<A<1)\)并提取全部小数部分，再用\(m\)乘上这部分，最后向下取整。这里有\(A,m\)两个常数需确定，\(m\)相当于系数对结果影响不大，通常选\(m = 2^p\)以方便二进制计算机用移位做乘法，对\(A\)的选择也是如此，计算机会根据其字长\(w\)先用\(s\)表示\(A = \frac{s}{2^w}\)，再把“乘\(A\)”变成“乘\(s\)并右移”，最后的二进制结果是\(sk\)低\(w\)位的高\(p\)位(如上图)。至于\(A\)怎么选，著名计算机学者Knuth认为\(A = \frac{\sqrt{5}-1}{2} = 0.618…\)是比较好的选择；
3) 全域哈希：使用多个哈希函数，随机选择哈希函数求哈希值。这使哈希值有“真正”的随机性，同个关键字可能算出不同的哈希值。这种随机性在安全上有优势，比如有黑客想用哈希冲突带来的性能下降拖垮服务器(DDOS)，黑客了解服务器用的哈希函数，所以他能构造导致冲突的关键字发起攻击。而全域哈希能有效降低这种风险；
哈希冲突的处理
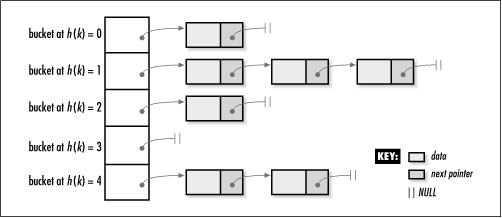1) 拉链法：在槽位上用链表来存储元素，具体如上图1。该方案下每个槽能放多个元素，一般会形象得把槽改称为桶(bucket)。既然用了链表，查找元素时就可能要遍历某槽的链表(桶)，对于有\(m\)个桶，当前有\(n\)个元素的拉链法哈希表，如果其哈希函数满足简单均匀，那么查找删除的最坏代价都是\(O(1 + \frac{n}{m})\)。实际应用中槽数和容量基本是成比例的，所以也认为其等于\(O(1)\)。加入元素时，由于可直接插入链表表头，所以最坏代价是\(O(1)\)。拉链法哈希表可存放无限个元素；
2) 开放寻址法：简单来说就是槽位被占用时用其他哈希的槽位。寻找可用空槽的过程称为探查(probe)，探查不一定是按索引递增的，可具体针对每个关键字设计探查顺序，形式上可把其并入哈希函数\(h(k,s)\)，其中\(k\)是关键字，\(s\)称为探查号。设槽数为\(m\)若\(h(k,0)\)被占则继续探查\(h(k,1)\)，也被占则继续探查直到\(h(k,m-1)\)。注意\(s\)从\(0\)到\(m-1\)不是指从\(0\)号槽顺序探查到\(m-1\)号槽，对不同\(k\)，\(s\)从\(0\)到\(m-1\)对应不同的槽的排列。\(h(k,0)\)相当于原来的\(h(k)\)。对于查找和插入，根据\(h\)按同样次序探查并验证关键字即可，但对于删除则要考虑其他关键字的影响，比如插入时发现\(h(k,i)\)位置被占用，则会继续探查，但如果之后某删除操作删掉\(h(k,i)\)元素，那再之后查找\(k\)时会因为\(h(k,i)\)为空而误判\(k\)不存在，像这种情况必须考虑到。另外这种带探查策略的哈希函数更难保证简单性和均匀性，下面看几种带探查策略的哈希函数：
2.1) 一次探查：设辅助哈希函数\(h_1\)是映射到\(0\)到\(m-1\)号槽位的，线性探查哈希函数为\(h(k,i) = (h_1(k) + i)~\%~m\)。这是最简单的探查策略，就是前面说的按递增顺序去探查下一个槽位，直到绕一圈后回到\(h_1(k) – 1\)槽位。这种策略下若任意空槽前有连续\(n\)个非空槽，该槽下次被占的概率就是\(\frac{n+1}{m} \)，说明会趋向于占用连续槽位，占用连续槽位意味着连续的多次探查，会影响性能。这种槽位聚集的现象称为群集，一次探查带来的群集称为一次群集；
2.2) 二次探查：二次探查改进哈希函数为\(h(k,i) = (h_1(k) + c_1i + c_2i^2)~\%~m\)，这种哈希函数能更好的改善群集，但对于初始探查位置相同的2个关键字，它们的探查次序是完全相同的，由于一共只有\(m\)个初始探查位置，所以二次探查一共只能给出\(m\)种探查次序的排列，而槽位的排列是有\(m!\)种的，所以二次探查同样也有二次群集；
2.3) 双重哈希：最好的探查策略之一。需要加一个辅助哈希函数\(h_2\)，哈希函数为\(h(k,i) = (h_1(k) + ih_2(k))~\%~m\)，其中\(h_2\)与\(m\)互素，否则无法保证探查到每个槽。实际中常用如下2种简便方法保证\(h_2\)与\(m\)互素：
2.3.1) 取\(m\)为2的幂，\(h_2\)恒为奇数正整数；
2.3.2) 取\(m\)为素数，\(h_2\)为恒小于\(m\)的正整数。
实际中很少用这两者以外的方案来保证\(h_2\)与\(m\)的互素，因为比较难找到高效生成互素的\(h_2\)与\(m\)的实现。在双重哈希中，\(h_1\)决定首次探查的位置，\(h_2\)决定相邻两次探查的位置间隔，通过设计\(h_2\)可以让间隔取\(1\)到\(m-1\)的值，所以良好设计的哈希函数能提供至少\(O(m^2)\)种探查次序的排列，其相比一次二次探查的\(O(m)\)有更轻的群集。然后简单说明下这种策略的代价，这里不针对上述3种具体的探查策略，而是假定哈希函数满足“每个关键字的探查序列等可能的是所有槽位排列中的任一种”。对于\(m\)个槽，当前有\(n\)个元素的这种哈希表，一次成功或不成功的查找最多探查\(O(\frac{m}{m-n})\)次，这里不证明了。
3) 完全哈希法：简单来说就是再加一级哈希，把每个槽都改放一个二级哈希表，元素会被放入不同的二次哈希表，每个二次哈希表有自己的哈希函数\(h_j\)(\(j\)是槽编号)。这种方案一般要保证每个二级哈希表都无冲突，这些保证无冲突的方法会导致二级哈希表槽位数是一级哈希过来的关键字数的平方。但通过精心设计一级函数，是可以让整体空间保持在\(O(n)\)的。这里不具体讨论完全哈希，总之其有不错的平均代价，特别是对于元素存储后就不再修改的静态哈希表；
下面实现双重哈希的开放寻址哈希表，槽数\(m\)取素数701，\(h_1(k) = k~\%~m = k~\%~701\)，\(h_2(k) = 1 + (k~\%~700)\)为辅助哈希函数，\(h_2\)的最大值刚好小于\(m\)，所以\(h_2,m\)互素。这里会用\(Node\)对象包装元素，这是为记录插入时对应的关键字、该\(Node\)是否曾被删除。这2个信息很重要，借助它们才能正确高效的完成查找、插入、删除的操作。另外Python本身内置了多种“基于哈希表”的数据类型，最常用的就是set和dict，遇到使用哈希表的算法时，可直接用这些数据类型实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | class Node: def __init__(self, key = None, value = None): self.key = key self.value = value self.isDeleted = False class HashTable: def __init__(self): self.m1 = 701 self.m2 = 700 self.arr = [ Node() for i in range(self.m1) ] def h1(self, k): return k % self.m1 def h2(self, k): return 1 + (k % self.m2) def h(self, k, i): return (self.h1(k) + i * self.h2(k)) % self.m1 def get(self, k): for i in range(self.m1): node = self.arr[self.h(k, i)] if node.key is None: break if not node.isDeleted and node.key == k: return node.value raise Exception('关键字不存在') def set(self, k, v): for i in range(self.m1): node = self.arr[self.h(k, i)] if node.key is None or node.isDeleted or node.key == k: node.key = k node.value = v node.isDeleted = False return raise Exception('表已满') def remove(self, k): for i in range(self.m1): node = self.arr[self.h(k, i)] if node.key is None: break if not node.isDeleted and node.key == k: node.isDeleted = True return raise Exception('关键字不存在') |