有向图的连通性
1) 转置图:把有向图所有边逆转方向得到的图;
2) 基图:有向图去掉边的方向后所得到的无向图;
3) 有向弱连通图:若有向图\(G\)的基图是无向连通图,则\(G\)为有向弱连通图;
4) 有向单连通图:若有向图\(G\)的任意两顶点\(u,v\)满足从\(u\)可达\(v\)或从\(v\)可达\(u\),则\(G\)为有向单连通图;
5) 有向强连通图:若有向图\(G\)的任意两顶点\(u,v\)满足从\(u\)可达\(v\)且从\(v\)可达\(u\),则\(G\)为有向单连通图;
6) 强连通分量(SCC):有向图的一个极大的有向强连通子图,SCC最小为1个顶点,最大为整个图;
结合之前讨论的无向图连通性与上述定义,可了解有向图连通性的概念。下面研究SCC以及如何通过算法求出有向图上的全部SCC,这称为把有向图分解为SCC。通常把1个SCC记录为1个顶点集合。
另外,本文约定用邻接表来描述有向图。
Kosaraju算法
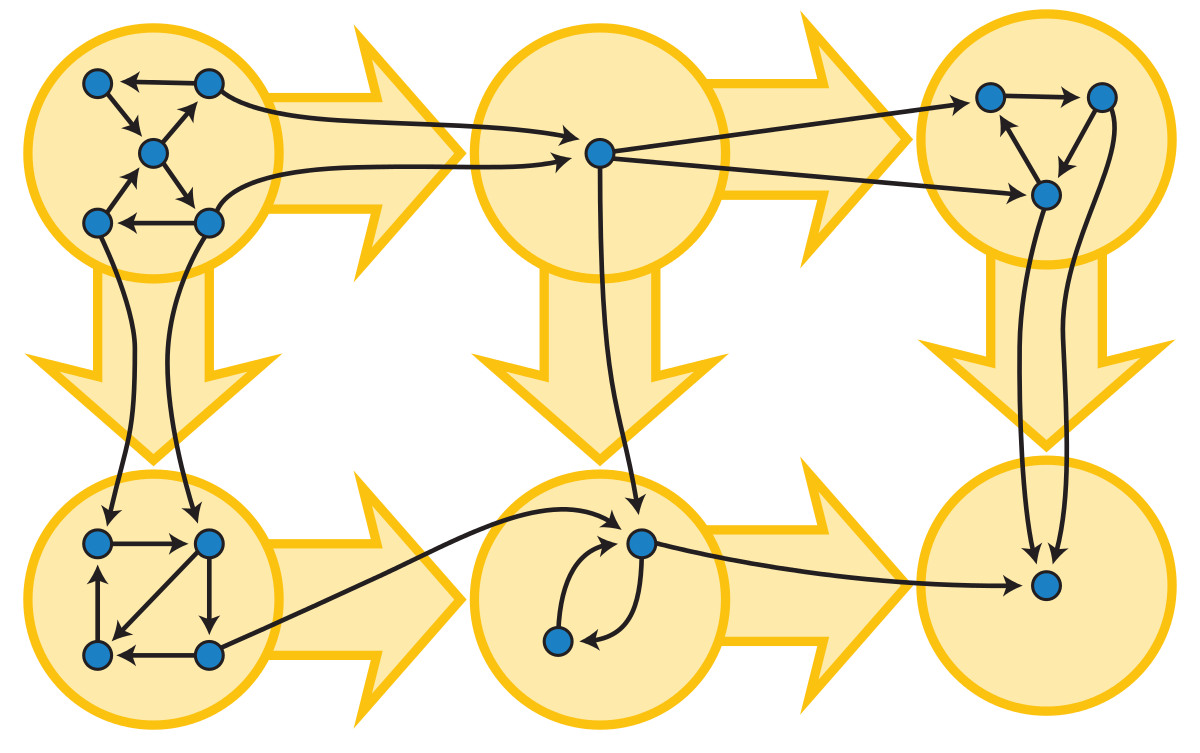
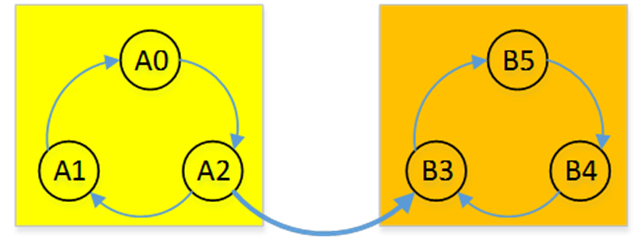
设对\(G\)执行了完整的DFS,其顶点都记录有染黑时间\(t_2\),而\(C_1,C_2\)是\(G\)的两个SCC,这里约定\(t_2\)还可以表示SCC的染黑时间,即可以用记号\(t_2(C_1)\)表示\(C_1\)顶点中最大的\(t_2\)。给出引理:
a) \(G\)中不能同时存在\(C_1\)->\(C_2\)与\(C_2\)->\(C_1\)的路径;
b) 设\(G\)的转置图为\(G_T\),\(G\)与\(G_T\)的所有SCC都相等;
证明:这点借上图来证明。首先对于某个圈圈(强连通分量)里面的所有边,其中任意两个顶点\(u,v\)互相到达,而且这些可达的路径必然都在圈圈内部,否则会违反上述的(a)。所以可以把圈圈里面的边全部逆转,这样原来的\(u-v\)和\(v-u\)路径刚好反过来还是互相可达的。然后再看圈圈之间的边,由于任意两个圈圈间(任意两个强连通分量中的顶点)不能互相抵达,所以逆转这些边后还是不能互相抵达(否则再逆转一次就变回原图而且能互相抵达了…)。所以逆转全部边不改变任意一个SCC。
c) \(G\)若存在\(C_1\)->\(C_2\)的边则\(t_2(C_1) > t_2(C_2)\),\(G^T\)若存在\(C_1\)->\(C_2\)的边则\(t_2(C_1) < t_2(C_2)\);
证明:若\(C_1\)与\(C_2\)中首个被染灰顶点\(x\)位于\(C_1\),在\(x.t_1\)时由白色路径定理\(C_2\)顶点集为DFS树中\(x\)的后裔,由后代区间嵌套得\(t_2(C_1)=x.t_2>t_2(C_2)\)。若\(x\)位于\(C_2\)中由于存在\(C_1\)->\(C_2\)的边,根据(a)不存在\(C_2\)->\(C_1\)路径,故直到\(x\)的子DFS结束\(x\)被染黑\(C_1\)的顶点都尚为白色,由于\(C_2\)为SCC故\(x\)被染黑时\(C_2\)的顶点都已染黑,故\(t_2(C_1) > t_2(C_2)\)。对于\(G^T\)由转置图定义知\(G\)存在\(C_2\)->\(C_1\)的边,问题化为前一个问题。
然后按\(t_2\)从大到小排列顶点得到序列\(L\),任意SCC的全部顶点在\(L\)上显然是从左到右分布的。然后看\(L\)左边第1个顶点(计作\(l_1\)),其一定是某个SCC(计为\(C_1\))中的最晚染黑顶点,根据(c)可知\(G\)中的其他SCC一定没有边连向\(C_1\),而\(G_T\)中则是\(C_1\)一定没有边连向其他SCC,也就是说如果从\(G_T\)上的\(l_1\)执行DFS,那么得到的生成树上的全部节点刚好是\(C_1\)。然后继续在\(L\)向右找到第一个不属于\(C_1\)的顶点(计为\(l_2\)),\(l_2\)一定是另个SCC(计为\(C_2\))的最晚染黑顶点,此时可以确定\(C_2\)一定有边连向\(C_1\)或是根本没有边连向其他SCC的,如果继续刚刚的DFS的话会得到另一个生成树,这个生成树的全部节点又刚好是\(C_2\)……继续这个过程,整个DFS过程会形成DFS森林,森林中的每个树就是一个SCC。将其整理为如下步骤:
1) 从\(G\)的任意顶点执行DFS直到所有顶点染黑,并用序列\(L\)记录染黑次序;
2) 反转序列\(L\);
3) 计算出\(G\)的转置图\(G_T\);
4) 在\(G_T\)上执行“按\(L\)遍历节点的DFS”,即从左到右逐个对\(L\)的白色节点执行子DFS;
5) 算法结束后每1个DFS树就是1个SCC;
该算法的代价同阶于DFS的代价等于\(O(|V|+|E|)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 | def revert(adj): adj_T = { u:set() for u in adj} for u in adj: for v in adj[u]: adj_T[v].add(u) return adj_T def dfs(adj, u, grey, black): if u not in grey: grey.add(u) for v in adj[u]: dfs(adj, v, grey, black) black.append(u) def kosaraju(adj): grey = set() black = list() for u in adj: dfs(adj, u, grey, black) black.reverse() adj_T = revert(adj) grey = set() result = list() for u in black: scc = [] dfs(adj_T, u, grey, scc) if len(scc) > 0: result.append(scc) return result print(kosaraju({ })) print(kosaraju({ 'a': {}, 'b': {}, })) print(kosaraju({ 'a': { 'b' }, 'b': { 'a' }, })) print(kosaraju({ 'a': { 'b' }, 'b': { 'c' }, 'c': { 'a', 'h' }, 'e': { 'f' }, 'f': { 'g' }, 'g': { 'e' }, 'h': { 'f' }, 'i': {} })) |
Tarjan算法
 (p1)
(p1)
 (p2)
(p2)
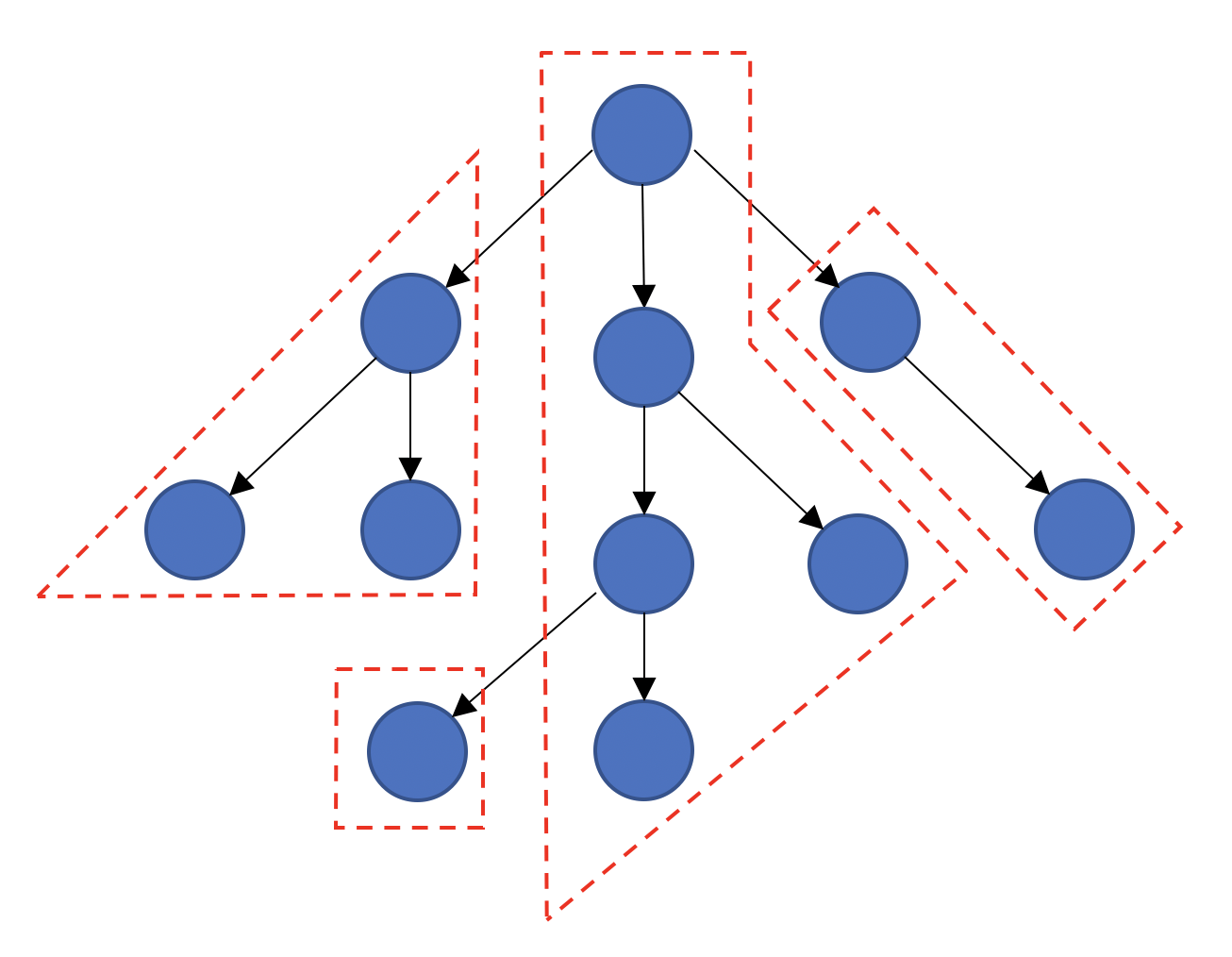
Kosaraju算法通过特殊的子DFS次序使每个DFS树等于每个SCC,而Tarjan算法则可基于任意DFS。SCC在任意DFS森林的分布如上图p1红虚线。同个SCC顶点位于同个DFS树(用白色路径定理易证),且这个DFS树上的SCC的“根”到其他SCC顶点的路径一定不途径任何非该SCC的顶点(若存在这样的顶点那么它就一定可以与该SCC互相可达从而导致矛盾)。SCC的分布是Tarjan算法依赖的重要性质。
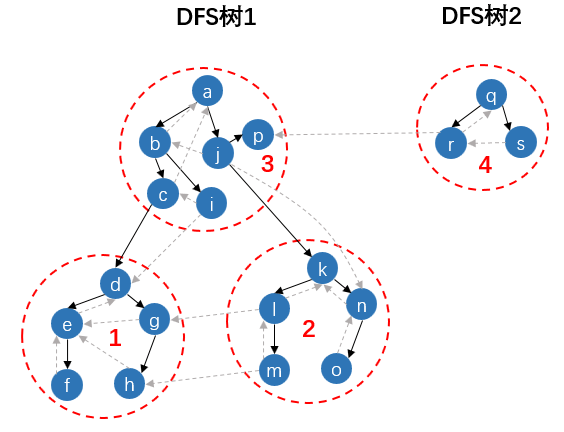
然后再来看DFS森林上SCC之间的边关系。如上图p2所示,字母代表节点染灰的次序、实线代表树边、虚线代表所有非树边,红色虚线代表一个SCC,红色序号代表SCC全部染黑的次序。SCC间可通过树边、正向边、横向边连接,但不能通过反向边连接,因为反向边会连通两个SCC导致矛盾。任意SCC的节点在被其上的子DFS发现连向其他SCC的非树边的时刻,这个其他SCC的所有顶点一定都已染黑。
为了方便讨论这里定义几个记号:
1) \(scc(x)\):节点\(x\)所在的SCC的全部顶点;
2) \(sub(x)\):节点\(x\)及其沿着树边可达的属于\(scc(x)\)的全部顶点;
3) \(top(x)\):节点\(x\)所在SCC的“根”;
然后给出Tarjan算法中的DFS辅助量:
1) \(dfn[u]\):记录\(u\)是第几个染灰的;
2) \(low[u]\):“\(sub(u)\)所有节点的\(dfn\)”与“\(sub(u)\)所有节点沿1条非树边边可达的\(scc(u)-sub(u)\)的所有顶点的\(dfn\)”中的最小值。对任意顶点\(u\),若\(u\)不是SCC的根,则\(low[u] < dfn[u]\)。因为\(sub(u)\)必须有节点能沿1条反向边或横向边可达\(scc(u) – sub(u)\),否则\(sub(u)\)和\(scc(u)-sub(u)\)无法连通。若\(u\)是SCC的根,则\(sub(u)=scc(u)\),容易得出\(low[u] = dfn[u]\);
3) \(stk\):在DFS过程中存放“满足条件”的已染灰顶点。规定“任意顶点染灰时刻入栈,染黑时刻若发现顶点(计为\(u\))满足\(dfn[u] =low[u]\)。则循环出栈,直到\(u\)出栈”。根据SCC的分布特征,以及上述(2)对\(low\)的定义和分析,可以知道每一次循环出栈从开始到结束,出栈的所有顶点刚好就是某个SCC的全部顶点;
考虑构造能够正确维护这些辅助量的DFS算法。最容易维护的就是\(dfn\),只需在染灰时刻记录次序即可。而\(low\)必须在顶点“染灰之后,染黑之前”被正确计算,这样才能通过比较\(low,dfn\)并且借\(stk\)分割出SCC。下面给出Tarjan算法中每个顶点(计为\(u\))的子DFS的流程步骤:
1) 记录\(dfn[u]\),把\(u\)入栈\(stk\),初始化集合\(S = \{dfn[u]\}\);
2) 遍历\(u\)的每个邻接点\(v\);
2.1) 若\(v\)未在\(dfn\)中,则对\(v\)进行子DFS,之后把\(low[v]\)加入\(S\);
2.2) 若\(v\)已在\(dfn\)中且\(v\)在\(stk\)中,则把\(dfn[v]\)加入\(S\);
3) 记录\(low[u] = min(S)\);
4) 若\(low[u]=dfn[u]\)则循环出栈直到\(u\)出栈,把该步骤所有出栈顶点记录为一个SCC;
下面来讨论上述流程的正确性,这里不妨直接跑一遍上述算法。首先可以确定这个Tarjan的DFS可以得到和标准DFS完全一样的生成森林。\(low,stk,dfn\)不过是在标准DFS的基础上额外记录一些信息,不影响DFS的次序。这里不妨看上图p2,假设这就是Tarjan的DFS得到的森林。然后来看顶点d的子DFS开始的时刻,此时\(d\)刚染灰,\(stk=[a,b,c,d]\)。然后再让算法一直跑到\(d\)即将要染黑的时刻,在这段时间里,该SCC的任何节点的子DFS在沿非树边发现邻接点时,这些邻接点都在\(stk\)中,又都指向\(scc(d)\)的其他顶点。所以其中任意顶点\(u\)的子DFS在结束时都访问了\(sub(u)\)所有顶点的所有可达\(scc(u)-sub(u)\)的非树边,也就是说这些节点都正确的计算出了自己的\(low\)。那么\(d\)即将要染黑的时刻可以正确计算出\(low[d]\),接着就会导致执行步骤(4),整个\(scc(d)\)出栈。
当然这个SCC是比较特殊的,它是第一个DFS树上的第一个叶子SCC,它没有连向其他SCC的边。这个时候就体现不出\(stk\)的作用。然后继续跑算法步骤,顶点c沿着在d的子DFS结束,\(c\)遍历完其邻接点后即将计算\(low[c]\)可以发现这条\((c,d)\)树边不会影响到\(low[c]\)的计算,因为\(low[d]=dfn[d] < dfn[c]\)。然后\(scc(c)\)中\(j\)节点的子DFS会发现一个指向\(scc(d)\)的正向边,但由于\(scc(d)\)已经退栈所以这个边被忽略掉。同理对于节点\(l,m,r\)也是一样。
所以对于任意SCC中的任意节点\(x\)在子DFS时发现的沿非树边可达的、且处于\(stk\)中的邻接点等于\(x\)沿非树边可达的其他\(scc(x)\)顶点。那么\(x\)的子DFS在即将染黑\(x\)时就一定能访问过所有\(sub(x)\)节点的所有沿1条非树边可达的\(scc(x)-sub(x)\),也就是此刻能求出正确的\(low[x]\),于是在此刻做\(low[x]=dfn[x]\)的判断如果确定\(x\)是SCC的根的话循环出栈就能得到整个\(scc(x)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 | class Stack: def __init__(self): self.l = list() self.d = dict() def push(self, value): self.l.append(value) if value not in self.d: self.d[value] = 0 self.d[value] += 1 def pop(self): value = self.l.pop() self.d[value] -= 1 if self.d[value] == 0: self.d.pop(value) return value def has(self, value): return value in self.d def dfs(result, adj, u, dfn, low, stk): dfn[u] = len(dfn) + 1 stk.push(u) low[u] = dfn[u] for v in adj[u]: if v not in dfn: dfs(result, adj, v, dfn, low, stk) low[u] = min(low[u], low[v]) elif stk.has(v): low[u] = min(low[u], dfn[v]) if low[u] == dfn[u]: scc = [] while True: node = stk.pop() scc.append(node) if node == u: break result.append(scc) def tarjan(adj): result = list() dfn = dict() low = dict() stk = Stack() for u in adj: if u not in dfn: dfs(result, adj, u, dfn, low, stk) return result print(tarjan({ })) print(tarjan({ 'a': {}, 'b': {}, })) print(tarjan({ 'a': {'b'}, 'b': {'a'}, })) print(tarjan({ 'a': {'b'}, 'b': {'c'}, 'c': {'a', 'h'}, 'e': {'f'}, 'f': {'g'}, 'g': {'e'}, 'h': {'f'}, 'i': {} })) |