并查集与并查集森林

并查集(Union-find Disjoint Sets)

首先定义不相交集合数据结构(Disjoint-Sets Data Structure)，其首先是一个集合\(S = \{S_1,S_2,…,S_n \}\)，\(S\)中的元素也是集合，并且对于\(S\)中的任意两个元素\(S_x,S_y\)，都满足\(S_x\cap S_y=\emptyset\)。并查集则是带有特定运算的不相交集合数据结构，主要用于解决查询与合并的问题，由于\(S_x\)是可修改的，所以也称它们为动态集合。并查集运算的定义如下：

1) \(MAKE(x)\)：创建1个仅含元素\(x\)的动态集合，并把该动态集合加入到并查集中；

是若干不相交动态集合组成的集合\(S = \{S_1,S_2,…S_n \}\)，不相交指任意两动态集合间无重复元素，从动态集合中任取一元素即可形成与该动态集合的单射。对并查集中的动态集合\(S_k\)而言，动态指\(S_k\)中的元素是从无到有通过\(S\)上定义的运算结构动态添加的，所以接下来讨论\(S\)上的运算结构：

\(MAKE(x)\)：新建动态集合，加入元素\(x\)并选其为动态集合的唯一“代表”；

\(UNION(x,y)\)：把包含\(x\)的动态集合与包含\(y\)的动态集合合并；

\(FIND(x)\)：返回包含\(x\)的动态集合的“代表”；

并查集提供的运算结构相对抽象，下面利用上述接口求无向图的连通分量(但先不考虑上述接口的实现):

1) 遍历\(G\)的顶点集，对每个顶点执行\(MAKE\)；

2) 遍历\(G\)的边集顶点对，若两顶点执行\(FIND\)的结果不同，则对两顶点执行\(UNION\)；

3) 最终并查集中的每个动态集合为每个连通分量；

并查集链表

如上图所示，并查集中的每个动态集合被存储为链表。运算结构在并查集链表上的实现如下。

\(MAKE(x)\)：在并查集中新建动态集合，head与tail都指向以\(x\)初始化的链表节点，代价为\(O(1)\)；

\(FIND(x)\)：由于每个链表节点都有指向所属动态集合的指针，所以代价为\(O(1)\)；

\(UNION(x,y)\)：把\(y\)所属链表合到\(x\)所属链表。需遍历\(y\)的所属链表节点，使每个节点都指向\(x\)所属动态集合。对形如\([…MAKE(x_2),UNION(x_2,x_1),MAKE(x_3),UNION(x_3,x_2)…]\)的操作序列，每次都是把长链表合并到新建的单节点链表上。这样\(UNION\)的摊还代价为\(O(n)\)，故存在操作序列能得到\(O(n^2)\)的总代价；

考虑通过“加权合并的启发式策略”优化：“\(UNION\)前预先判断两链表长度，把长链表接到短链表上”。在该优化下空并查集链表上执行\(m\)元素操作序列(其中\(n\)个\(MAKE\))的代价上界为\(O(m+nlgn)\)。启发式策略通常是指“符合直觉，但不一定能严格估计出复杂度”的策略，也就是说

证明：记录所有链表节点指向“所属动态集合指针”的变化次数，该指针变化仅发生于\(UNION\)运算。设\(x\)为并查集中的任意元素(链表节点)，\(x\)第1次指针变化后并查集有至少2个元素，第2次有至少4个元素…依次类推\(x\)的指针变化\(k\)次后并查集至少有\(2^k\)个元素。由于元素总数(\(MAKE\)总次数)为\(n\)，故任意链表节点的“所属动态集合指针”至多变化\(lg(n)\)次。故使并查集的最终总元素数为\(n\)的任意操作序列，\(UNION\)与\(MAKE\)带来的最坏总代价是\(O(nlg(n))\)。对于\(FIND\)运算，其带来的总代价有上界\(O(m)\)。综上对任意操作序列其最坏代价为\(O(m+nlgn)\)。

并查集森林

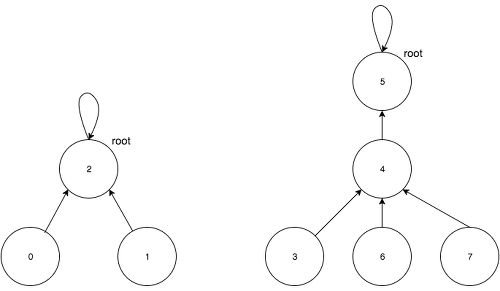
并查集森林的实现如上图所示，树表示动态集合，树根表示动态集合的“代表”。其运算结构实现如下：

\(MAKE(x)\)：在森林中新建树(树根)；

\(FIND(x)\)：从\(x\)向父节点回溯，直到找到树根将其返回；

\(UNION(x,y)\)：把\(y\)所在树根的父节点指向\(x\)所在的树根；

并查集森林也需要“按秩合并”与“路径压缩”的启发式策略，否则其不如带启发式策略的并查集链表。

秩：在节点上记录秩(rank)表示该子树的高度上界；

按秩合并：UNION时把小秩树合到大秩树上(让节点少的指向节点多的)，类似并查集链表的加权合并；

路径压缩：FIND时把回溯途径的节点都直接指向树根，但不得改变或违反任何节点的秩；

并查集森林在附加“按秩合并”与“路径压缩”策略后的运算结构实现如下。

\(MAKE(x)\)：为通过\(x\)初始化的新树根额外添加变量\(rank=0\)；

\(UNION(x,y)\)：两者秩不相等时把小秩树合到大秩树上，相等时任意合并但需把新树根的秩加1；

\(FIND(x)\)：该运算额外实现“路径压缩策略”的物理实现依靠了“两趟式递归”，即每次进入递归就找一次当前节点的父节点，每次退出递归(回溯)都返回树根，且把当前节点的父节点修改为树根。这样的最终结果是返回元素所在动态集合的树根，且把元素到树根的“途经节点”都“平铺”为树根的第二代节点；

注意到代码从\(UNION\)中拆分出\(LINK\)运算，这仅是为接下来的复杂度分析做更方便的表述。

阿克曼函数与反阿克曼函数

\(
\begin{equation}
(1)~~A_k(j)=
\begin{cases}
j+1& \text{k = 0}\\
A_{k-1}^{(j+1)}(j)& \text{k > 0}
\end{cases}
\end{equation}
\\{~}\\{~}\\
\begin{equation}
(2)~~A_{k}^{(i)}(j)=
\begin{cases}
j& \text{i = 0}\\
A_{k}^{(1)}(A_{k}^{(i-1)}(j))& \text{i > 0}
\end{cases}
\end{equation}
\\{~}\\{~}\\
\begin{equation}
(3)~~~~
\begin{cases}
A_1(j)=2j+1\\
A_2(j)=2^{(j+1)}(j+1)-1\\
\end{cases}
\\{~}\\{~}\\
(4)~~~~
\begin{cases}
A_3(1)=A_2^{(2)}(1)=A_2(7)=2047\\
A_4(1)=A_3^{(2)}(1)=A_3(2047) >> A_2(2047) > 2^{2048} = 16^{512} >> 10^{80}\\
\end{cases}
\\{~}\\{~}\\
(5)~~~\alpha(n)=min\{k|A_k(1)\geq n\}
\\{~}\\{~}\\
\begin{equation}
(6)~~~\alpha(n)=
\begin{cases}
0& {0 \leq n \leq 2}\\
1& {3 \leq n \leq 3}\\
2& {4 \leq n \leq 7}\\
3& {8 \leq n \leq 2047}\\
4& {2048 \leq n \leq A_4(1)}\\
\end{cases}
\end{equation}
\\{~}\\
\end{equation}
\)

阿克曼(Ackermann)函数是种特殊函数，其是递归函数但非原始递归函数。该函数用于并查集森林的时间复杂度分析。

在上述(1)中定义了阿克曼函数\(A_k(j)\)，其中\(k\geq 0\)与\(j>0\)都为整数，在该定义中使用了函数的迭代(复合)记号，例如\(f^{(3)}(x) = f(f(f(x)))\)与\(f^{(1)}(x)=f(x)\)。如果扩充函数的迭代(复合)记号，使得\(f^{(0)}\)有数学意义，那么\(A_{k}^{(i)}(j)\)满足上述(2)，称\(k\)为\(A\)的级(level)。在(3)中给出了函数\(A_1(j)\)与\(A_2(j)\)的闭合形式表示，对其证明如下：

3.1) 归纳基础\(A_0^{(0)}(j)=j+0\)，归纳假设\(A_0^{(i-1)}(j)=j+(i-1)\)，需证明假设成立时\(A_0^{(i)}(j)=A_0^{(1)}(A_0^{(i-1)}(j))\)。\(A_0^{(i)}(j)=A_0(j+(i-1))=(j+(i-1))+1=j+i\)，归纳成立。\(A_1(j)=A_0^{(j+1)}(j)=j+(j+1)\)。

3.2) 归纳基础\(A_1^{(0)}(j)=2^{0}(j+1)-1\)，假设\(A_1^{(i-1)}(j)=2^{(i-1)}(j+1)-1\)，证假设成立\(A_1^{(i)}(j)=A_1^{(1)}(A_1^{(i-1)}(j))\)。\(A_1^{(i)}(j)=2(A_1^{(i-1)}(j))+1=2(2^{(i-1)}(j+1)-1)+1=2^{(i)}(j+1)-1\)，归纳假设成立。\(A_2(j)=A_1^{(j+1)}(j)\)，\(A_2(j)=A_1^{(j+1)}(j)=2^{(j+1)}(j+1)-1\)。

在(4)中给出了\(A_4(1)\)与\(A_3(1)\)的数量级，相对容易验证\(A_k(j)\)随\(k,j\)严格递增，其中\(10^{80}\)为宇宙原子数目的估计数量级。对于整数\(n\geq 0\)，定义关于\(A_k(n)\)反函数的反阿克曼函数\(\alpha(n)\)如(5)所示。用该定义易得出(6)中\(\alpha(n)\)的部分函数值，可以发现\(A_4(1)\)已可以看作是“正无穷”。所以在非数学的算法范畴下，不严谨的约定\(\alpha(n)\leq 4 = O(1)\)。

并查集森林的时间复杂度

对并查集森林的计算复杂性分析最早是Tarjan给出的，分析的结果是如下定理：

定理：空并查集森林的\(m\)元素操作序列(有\(n\)个\(MAKE\))的最坏代价为\(O(m\alpha(n))\)。

说明：\(UNION\)可拆分为两次\(FIND\)与一次“按秩合并”，把“按秩合并”计为\(LINK\)。任意序列的\(UNION\)被置换为\(FIND,FIND,LINK\)，可将问题转为是关于\(MAKE,FIND,LINK\)所任意组成的操作序列的。另外对于本证明中出现的\(A_k\)与\(\alpha\)，其分别为\(k\)级阿克曼函数与反阿克曼函数。

在讨论前先给出较易得的“秩性质”引理：

1.1) 对任意节点\(x\)，若其存在父节点则\(x.p.rank>x.rank\)；

1.2) 对任意节点\(x\)，当\(x\)变为子节点后\(x.rank\)不再变化；

1.3) 对任意节点到树根的路径，秩是严格递增的；

1.4) 任意节点的秩存在一个\(n-1\)的上界；

利用势能摊还分析并查集森林的代价，定义节点\(x\)在第\(q\)个操作后的势能为\(\phi_q(x)\)，定义并查集森林在第\(q\)个操作后的势为\(\Phi_q=\sum_{x} \phi_q(x)\)。定义\(x\)为树根或\(x.rank=0\)时\(\phi_q(x)=\alpha(n)\cdot x.rank\)，剩余问题是定义其他情况的\(\phi_q(x)\)。所以在对下述势能的讨论中，任意节点\(x\)都为非树根节点且\(x.rank \geq 1\)，并为此定义两个辅助函数：

\(
\begin{equation}
level(x)~:=~max\{k|x.p.rank \geq A_k(x.rank) \} \\
x.p.rank\geq x.rank + 1 = A_0(x.rank) ~=>~ level(x)\geq 0 \\
A_{\alpha(n)}(x.rank)\geq A_{\alpha(n)}(1) \geq n > x.p.rank ~=>~ level(x)<\alpha(n) \\
0 \leq level(x) < \alpha(n)
\end{equation}
\\
{~~}
\\
{~~}
\\
\begin{equation}
iter(x)~:=~max\{i|x.p.rank \geq A_{level(x)}^{(i)}(x.rank) \} \\
x.p.rank\geq A_{level(x)}^{(1)}(x.rank) ~=>~ iter(x)\geq 1 \\
A_{level(x)}^{(x.rank+1)}(x.rank) = A_{level(x)+1}^{(1)}(x.rank) > x.p.rank ~=>~ iter(x)<x.rank+1 \\
1\leq iter(x)\leq x.rank
\end{equation}
\)

\(level(x)\)的意义是非树根节点\(x\)，其能取得的阿克曼函数“最大级”，当该函数值小于其父节点的秩时。而\(iter(x)\)为对于该“最大级”函数，其至多可迭代的次数，当该迭代次数下的函数值小于其父节点的秩时。\(x.rank\)的值是不变的，但是\(x.p.rank\)有“可能”继续递增。\(level(x)\)与\(iter(x)\)有类似“反比”的关系。\(\phi_q(x)\)的完整定义：

\(
\begin{equation}
\phi_q(x)=
\begin{cases}
\alpha(n)\cdot x.rank & \text{x为树根或x.rank=0}
\\
(\alpha(n)-level(x))\cdot x.rank ~-~ iter(x) & \text{x非树根且x.rank>0}
\end{cases}
\end{equation}
\)

然后给出关于上述\(\phi_q(x)\)性质的“势引理”如下：

2.1) 利用性质与引理容易得出对任意节点\(x\)与计数\(q\)，有\(0 \leq \phi_q(x) \leq \alpha(n)\cdot x.rank \)；

2.2) 对任意非根节点\(x\)且\(x.rank>0\)与计数\(q\)，有\(\phi_q(x) < \alpha(n)\cdot x.rank \)；

2.3) 第\(q\)次运算为\(MAKE\)或\(LINK\)，对于任意非根节点\(x\)有\(\phi_q(x) \leq \phi_{q-1}(x)\)。并且当\(x.rank>0\)且在运算的前后函数值\(iter(x)\)或\(level(x)\)发生变化，则\(\phi_q(x)<\phi_{q-1}(x)\)。

非树根时\(x.rank\)不变，\(n\)已被操作序列确定故不变，故\(x.rank=0\)时\(\Delta\phi(x)=0\)，剩下\(x.rank>0\)的情况。由于\(x.p.rank\)可能增加，根据定义\(level\)可能递增。若\(level\)与\(iter\)不变\(\Delta\phi(x)=0\)。若\(level\)不变\(iter\)变大，\(\Delta\phi(x)\leq-1\)。若\(level\)变大根据定义与\(iter\)的界，\(\Delta\phi(x)\leq-1\)。

最后给出3种操作中每个操作的摊还代价：

3.1) \(MAKE\)的摊还代价为\(O(1)\)；

实际代价为\(O(1)\)，新节点的秩为0，故总势能变化\(\Delta\Phi = 0\)，摊还代价为\(O(1)\)。

3.2) \(FIND\)的摊还代价为\(O(\alpha(n))\)；

设回溯路径包含\(s\)个节点，实际代价为\(O(s)\)。该运算不导致任何节点的势增加，非根节点情况为引理(2.3)，对于根节点其势能根据定义同样不变。注意到所有非根且秩大于0的节点的\(level\)不大于\(\alpha(n)\)且为整数，所以在回溯路径的\(s\)个节点中，有至少\(s – \alpha(n) – 2\)个节点满足\(level\)值与其他节点相等，-2中一个是树根，一个是可能为叶节点的节点(其秩可能等于0)。下面证明这\(s – \alpha(n) – 2\)个节点在\(FIND\)结束后势能减1，考虑换种方式来表述这个问题。设\(x\)与\(y\)为这样一对\(level\)值相等的节点，其中\(y\)在\(x\)上方但非根节点，需证明\(FIND\)后\(x\)的势减1。在路径压缩前有：

\(
\begin{equation}
y.p.rank \\
\geq A_{level}(y.rank) \\
\geq A_{level}(x.p.rank) \\
\geq A_{level}( A_{level}^{(iter(x))}(x.rank)) \\
= A_{level}^{(iter(x)+1)}(x.rank)
\end{equation}
\)

路径压缩后\(x\)与\(y\)有相同父节点，故\(x.p.rank=y.p.rank\geq A_{level}^{(iter(x)+1)}(x.rank)\)。根据\(iter\)函数的定义，在路径压缩后若\(level(x)\)不变则\(iter(x)\)将至少增加1，否则\(level\)会增加，总之\(iter(x)\)或\(level(x)\)发生变化，由引理(2.3)有至少\(max\{0,s – \alpha(n) – 2\}\)个节点的势能至少减1，即势能至少下降\(max\{0,s – \alpha(n) – 2\}\)，用\(t\)表示摊还代价，\(C\)表示大于实际代价隐藏常数的一个常数。下面给出摊还代价的上界：

\(
\begin{equation}
t \\
\geq O(s)-max\{0,s – \alpha(n) – 2\} \\
\geq O(s)-(s-\alpha(n)-2) \\
\geq O(s)-C(s-\alpha(n)-2) \\
= -O(s)+C\alpha(n)+2C \\
t \\
\geq C\alpha(n)+2C \\
= O(\alpha(n))
\end{equation}
\)

3.3) \(LINK\)的摊还代价为\(O(\alpha(n))\)；

设\(y\)成为\(x\)的父节点，根据(2.3)的引理\(LINK\)前\(y\)与\(x\)的孩子在按秩合并后势能不会变大。由于\(x\)原本是树根，若\(x.rank=0\)那么根据定义\(\Delta\phi(x)=0\)，若\(x.rank>0\)那么\(x\)变为非根节点后根据(2.2)有\(\Delta\phi(x)\leq -1\)，故\(x\)的势能不会变大。\(y\)在运算前后都是根，若其秩不变则\(\Delta\phi(y)=0\)，否则\(\Delta\phi(y)=\alpha(n)\)。综上\(\Delta\Phi \leq \alpha(n)\)。由于\(LINK\)的实际代价显然是\(O(1)\)，故摊还代价有上界\(O(1)+O(\alpha(n))=O(\alpha(n))\)。

4) 已证明\(FIND,LINK,MAKE\)组成的任意\(k\)元素序列(其中\(n\)个\(MAKE\))，其总代价有上界\(O(k\alpha(n))\)。而由\(FIND,UNION,MAKE\)组成的\(m\)元素序列可转化为\(m’\)元素的上述序列，显然的有\(m’ \leq 3m\)，故该序列的总代价有上界\(O(m’\alpha(n))= O(m\alpha(n))\)。