斜堆

斜堆(Skew Heap)

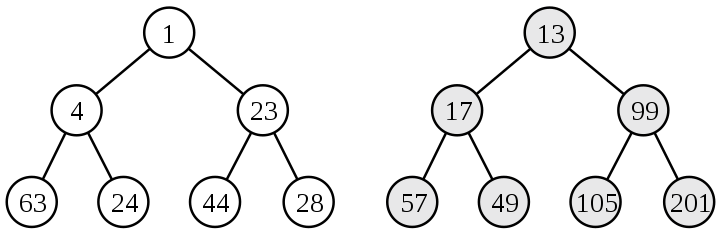
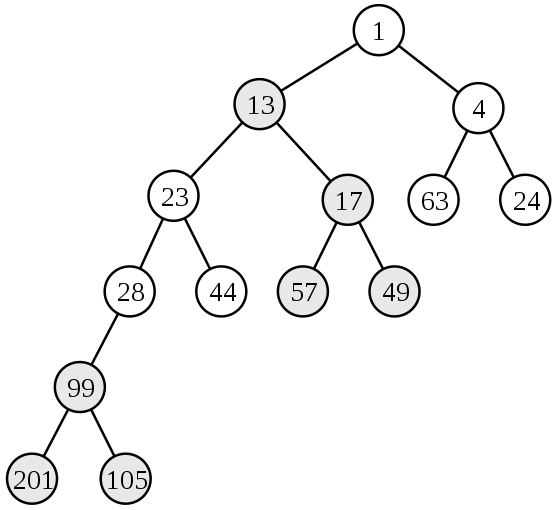
1986年美国学者Daniel Sleator和Robert Tarjan提出斜堆，这是种“松散”的左偏堆，其能保证运算的摊还代价是\(O(\lg{n})\)，但不保证每次运算的实际代价都是\(O(\lg{n})\)。斜堆和左偏堆的运算功能一致并且仅\(merge\)运算的步骤存在区别，斜堆的\(merge\)运算仍以左偏堆的为基础，但其在每次回溯都必须交换节点的左右孩子。这里不妨直接给出斜堆的运算步骤如下：

1) \(merge(r_1, r_2)\)：具体步骤分情况如下：

1.1) \(r_1,r_2\)不都非空：若\(r_1\)为空则返回\(r_2\)，否则返回\(r_1\)；

1.2) \(r_1,r_2\)都非空且\(r_1.key \leq r_2.key\)：置\(r_1.right=merge(r_1.right, r_2)\)。交换\(r_1\)的左右孩子。返回\(r_1\)；

1.3) \(r_1,r_2\)都非空且\(r_1.key>r_2.key\)：置\(r_2.right=merge(r_2.right, r_1)\)。交换\(r_2\)的左右孩子。返回\(r_2\)；

2) \(get()\)：若树根为空则抛异常。否则计树根为\(r\)，置\(k=r.key\)，然后置新树根为\(merge(r.left, r.right)\)，最后返回\(k\)；

3) \(put(k)\)：创建新节点\(x\)并置\(x.key=k\)，计树根为\(r\)，然后置新树根为\(merge(r, x)\)；

由于斜堆的\(merge\)运算总交换节点的左右孩子，所以无需在斜堆节点中继续存储和维护\(npl\)，但这也使得斜堆不再保证是左偏树，所以\(merge(r_1, r_2)\)运算本身无法保证有\(O(\lg{(npl(r_1))}+\lg{(npl(r_2))})\)的实际代价。需要注意到上述所有运算都适用于任何满足堆性质的二叉树，实际上如果对任意满足堆性质的二叉树多次的执行上述运算，那么每次运算的代价会逐步“收敛”至\(O(\lg{n})\)。斜堆的这种的特性跟Splay树十分相似，之后在分析斜堆的时间复杂度时会证明该特性。

斜堆的时间复杂度

定义二叉树中的重节点为右子树比左子树节点多的节点，相应的轻节点则为其他节点。轻节点满足如下性质：

a1) 对于包含\(n>0\)个节点的任意二叉树，其右链表中轻节点的数目至多等于\(1+\log_2{n}\)；

证明：将右链表中的轻节点自底向上的计为\(x_1,…,x_k\)，然后将\(x_1,…,x_k\)子树中的节点数依次计为\(n_1,…,n_k\)。根据轻节点的定义有\(n_{i+1} > 2n_i\)，进而有\(n_k \geq 2^{k-1}n_1 \geq 2^{k-1}\)。由于\(n\geq n_k\)所以\(n\geq 2^{k-1}\)。取对数可得\(k\leq 1+\log_2{n}\)。

定义摊还分析的势能函数\(\Phi(T)\)为二叉树\(T\)中重节点的总数。那么通过证明如下命题即可完成摊还分析：

b1) 对于\(merge(r_1, r_2)\)运算。若将其实际代价计为\(c\)。将其执行前\(r_1, r_2\)的势能分别计为\(\Phi_{1},\Phi_{2}\)，节点数分别计为\(n_{1},n_{2}\)。将其返回的二叉树的势能计为\(\Phi’\)。则存在常数\(A,B\)使得\(c+A(\Phi’-\Phi_{1}-\Phi_{2}) \leq 2A(\log_2{n_1}+\log_2{n_2}) + B\)；

证明：将执行前\(r_1\)和\(r_2\)的右链表中的轻节点和重节点的数目分别计为\(a_1,b_1\)和\(a_2,b_2\)，根据\(merge\)的步骤\(c\)不大于\(r_1\)和\(r_2\)的右链表长度之和的线性式\(C(a_1+b_1+a_2+b_2)+D\)。然后为方便讨论先规定递归回溯时不执行“交换左右孩子的步骤”，在该前提下若把整个过程步骤(1.2)或(1.3)返回的节点计为\(x_1…x_k\)，则整个过程前后仅\(x_1…x_k\)的轻重可能改变，因为所有其他子树在整个过程的前后不变，于是整个过程前后\(x_1…x_k\)的左子树不变但右子树节点增多，即\(x_1…x_k\)中的重节点仍是重节点但轻节点可能变重。然后考虑到“交换左右孩子的步骤”的影响，整个过程前后\(x_1…x_k\)中的重节点变为轻节点但轻节点可能变重，根据这点可得到\(\Phi’-\Phi_{1}-\Phi_{2} \leq -b_1-b_2+a_1+a_2\)，如果\(A\)足够大则有\(c+A(\Phi’-\Phi_{1}-\Phi_{2}) \leq 2A(a_1+a_2)+D\)。最后如果\(B\)足够大则结合上述(a1)即可得到不等式\(c+A(\Phi’-\Phi_{1}-\Phi_{2}) \leq 2A(\log_2{n_1}+\log_2{n_2}) + B\)。

b2) 在由\(n\)个节点组成的满足堆性质的二叉树上执行\(m\)次\(get,put\)运算，则其总代价有上界\(O(m\lg{(n+m)}+n)\)；

证明：将其中第\(k\)次运算前斜堆中的节点数计为\(n_k\)。若第\(k\)次运算是\(get\)，将其执行前后的斜堆的势分别计为\(\Phi,\Phi’\)，将其中所包含的\(merge\)运算的实际代价计为\(c\)，并将其执行前新节点的势计为\(\Phi_{new}\)。那么首先\(\Phi_{new}=0\)，然后结合(b1)可知该次运算的摊还代价为\(c+A(\Phi’-\Phi) = c+A(\Phi’-\Phi-\Phi_{new}) \leq 2A(\log_2{n_k}+\log_2{1}) + B\)。若第\(k\)次运算是\(put\)，将其执行前后斜堆的势分别计为\(\Phi,\Phi’\)，将其中包含的\(merge(r_1,r_2)\)的实际代价计为\(c\)，并将其执行前\(r_1, r_2\)的势和节点数分别计为\(\Phi_{1},\Phi_{2}\)和\(n’_{1},n’_{2}\)。结合(b1)有\(c+A(\Phi’-\Phi_{1}-\Phi_{2}) \leq 2A(\log_2{n’_1}+\log_2{n’_2}) + B\leq 4A\log_2{n_k} + B\)，考虑到\(\Phi_{1}+\Phi_{2}\leq \Phi\)可得到该次运算的摊还代价为\(c+A(\Phi’-\Phi) \leq 4A\log_2{n_k} + B\)。最后对于这\(m\)次运算，每次运算前总节点数都不超过\(n+m\)，由于\(\Phi\)最坏会从最开始的\(n\)降至0，故总摊还代价最坏比总实际代价少\(An\)。所以这\(m\)次运算的总代价上界是\(O(m\lg{(n+m)}+n)\)。

上述(b2)表明如果\(m\)很大，那么平摊到每次\(get,put\)运算上的实际代价为\(O(\lg{(n+m)})\)。

总结与实现

注意到上述步骤(1.2)和(1.3)是完全对称的，如果将步骤(1.3)替换成“返回\(merge(r_2, r_1)\)”，则其完全与原来的步骤(1.3)等价。而之所以在一开始这样定义步骤(1.2)和(1.3)，只是为了方便描述对算法步骤的分析。下面给出斜堆的程序实现。