单源最短路径
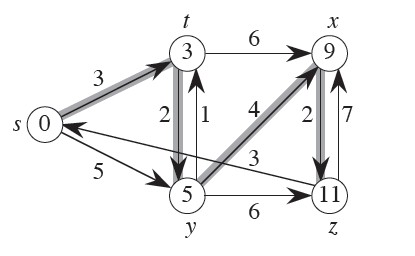
单源最短路:对有向图\(G=(V,E)\),边权\(w(E)\),源点\(s \in V\)。求\(s\)到\(V\)任意顶点的最短路。
最优子结构:若\(s-a-…-b-t\)为\(s\)到\(t\)的一个最短路,则上述\(a-…-b\)必为\(a\)到\(b\)的一个最短路。
负权环路:求最短路时需考虑边权函数\(w(E)\)为负值时的一般化情景。若\(s\)到\(v\)的所有路径中存在负权重环路,由于可在环路上任意的刷低权重所以\(\delta(s,v)=-\infty\)。但本文将讨论的算法并不会去处理这种情况,只能接收从原点到目标点的所有路径中不存在负权重环路的图。本文认为这种情况下的最短路无意义。
一般环路:负权环路的情况已经被排除,正权环路显然不可能出现在任何最短路径的结果中。最后剩下0权重环路情况,若其出现在某个最短路径中出现0权重环路,那么必然可以从该最短路径中“删去”环路得到同样权重的路径。综上可以认为求所有路径中的最短路径可以转化为求所有无环路径中的最短路径。
最短路径树:采用类似“最小生成树”的形式来记录结果,最短路径树中的每个节点只需记录父节点。
松弛操作
1) 在每个节点\(x\)初始化\(x.d=\infty\)作为最短路长度估计值,\(x.\pi=NONE\)作为最短路径树的估计前驱;
2) 松弛操作指检查边\((u,v)\)能否“改善”估计值\(v.d\),即测试是否有\(u.d+w(u,v) \leq v.d\),有则更新\(v.d\)与\(v.\pi\);
若源点到所有目标的所有路径都无负权环路,则有若干“符合直觉”的“松弛性质引理”如下。存在负权环路将使得引理“出现问题”,比如(1)有\((-\infty)-(-\infty)\leq 0\),(5)有无穷次松弛。这进一步明确负权环路图的“无意义”。
1) 三角不等式:\(\delta(s,v)\leq \delta(s,u) + w(u,v)\);
2) 上界性质:任意松弛操作后总有\( x.d \leq \delta(s,x)\),某次松弛后\( x.d = \delta(s,x)\),则\( x.d\)不再变化;
3) 非路径性质:若不存在到\(x\)的路径,则任意松弛操作后总有\( x.d = \infty\);
4) 收敛性质:若\(s-…-u-v\)为最短路,在\((u,v)\)松弛前有\(u.d=\delta(s,d)\),则松弛后永远有\(v.d=\delta(s,v)\);
5) 路径松弛性质:若\(v_1-…-v_k\)为最短路,且有松弛次序\((v_1,v_2),(v_2,v_3),(v_{k-1},v_k)\)。那么无论在这个次序中间“穿插”任何其他松弛操作,最终都有\(v_k.d=\delta(v_1,v_k)\);
6) 前驱子图性质:当所有节点\(x\)满足\(x.d=\delta(s,x)\)时,\(x.\pi\)记录了一个最短路径树;
下文的几种最短路算法都可看作是“松弛操作序列”,即几种按不同顺序与重复次数对图边进行松弛的策略。
Bellman-Ford算法
1) 遍历图边并对每条边执行松弛;
2) 重复(1)步骤\(|V|-1\)次;
3) 遍历图边\((u,v)\),若存在\(v.d>u.d+w(u,v)\)则图中有负权环路,否则算法执行成功;
Bellman-Ford算法允许负权边,其代价为\(O(|V||E|)\)。该算法是单源最短路问题的一般化解法,其不能接收原点到目标间有负权环路的图,但可以侦测到这种情况并报告错误。下面简单论证上述算法流程的正确性:
1) 算法的(1)与(2)可得到正确结果,若原点到目标点间无负权环路。因为原点若存在到目标点的最短路,则存在不含环路的最短路,不含环路的最短路至多经过\(|V|\)个顶点,其至多包含\(|V|-1\)条边。故对任意目标点\(v\)根据松弛引理(5)与排列组合关系,其存在对无环最短路的松弛次序使得\(v.d=\delta(s,v)\)。
2) 若(1)与(2)步得到正确结果,则(3)步由松弛引理(1),任意边\((u,v)\)满足\(v.d\leq u.d+w(u,v)\),算法执行成功;
3) 若(1)与(2)步未得正确结果,则假设\(s\)到任意顶点\(v\)的所有路径中存在负权环路\(v_0-v_1…v_k\)(其中\(v_k=v_0\)),顶点序列中的顶点满足\(v_i.d\leq v_{i-1}+w(v_{i-1},v_i)\)。首先考虑对两边求和有\(\sum_{i=1}^k v_i.d \leq \sum_{i=1}^k (v_{i-1}.d+w(v_{i-1},v_i))\),整理得\(\sum_{i=1}^k w(v_{i-1}.d,v_i) \geq \sum_{i=1}^k v_i.d ~- \sum_{i=1}^k v_{i-1}.d=0\),这与假设矛盾。故若\(s\)到任意顶点的所有路径中存在负权环路,环路中存在至少一条边\((u,v)\)满足\(v.d>u.d+w(u,v)\)。再结合上述的讨论(2)可以得出,若存在一条边\((u,v)\)使得\(v.d>u.d+w(u,v)\),则至少存在一个目标点使得\(s\)到该目标点的所有路径中存在一个负权环路。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | class Graph: def __init__(self): self.d = dict() def addVertex(self,i): self.d[i] = dict() def addEdge(self,i1,i2,w): self.d[i1][i2] = w def getWeight(self,i1,i2): return self.d[i1][i2] def getVertices(self,i): return self.d[i].keys() def vertices(self): return self.d.keys() def bellman_ford_relax(d,pi,graph,u,v): l = d[u] + graph.getWeight(u,v) if l < d[v]: d[v] = l pi[v] = u def bellman_ford(graph,s): d = {} pi = {} for v in graph.vertices(): d[v] = float('inf') pi[v] = None d[s] = 0 times = len(d) while times > 0: times -= 1 for u in d.keys(): for v in graph.getVertices(u): bellman_ford_relax(d,pi,graph,u,v) for u in d.keys(): for v in graph.getVertices(u): if d[u] + graph.getWeight(u,v) < d[v]: return False return d,pi |
用于无环图的算法
1) 将图顶点排序为拓扑序列\(L\);
2) 从左到右遍历\(L\)并松弛当前顶点的所有出边;
利用该基于拓扑排序的算法允许负权边,且每个边只松弛一次,代价为\(O(|V|+|E|)\)。算法的正确性较为直观,设\(s\)可达\(v\)则在\(L\)中\(v\)一定在\(s\)后面,并且\(s\)到\(v\)所有最短路的节点次序都符合\(L\)中这些节点的次序(符合拓扑序列定义)。由于\(L\)中\(s\)到\(v\)之间的所有节点都按拓扑次序把所有出边松弛化,根据松弛化引理(5)有\(v.d=\delta(s,v)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | class Graph: def __init__(self): self.d = dict() def addVertex(self,i): self.d[i] = dict() def addEdge(self,i1,i2,w): self.d[i1][i2] = w def getWeight(self,i1,i2): return self.d[i1][i2] def getVertices(self,i): return self.d[i].keys() def vertices(self): return self.d.keys() def topSortDfs(aov, vertex, white, black): for v in aov.getVertices(vertex): if v in white: white.remove(v) topSortDfs(aov, v, white, black) black.append(vertex) def topSort(aov): white = set(aov.vertices()) black = list() for v in aov.vertices(): if v in white: white.remove(v) topSortDfs(aov, v, white, black) black.reverse() return black def dag_relax(d,pi,graph,u,v): l = d[u] + graph.getWeight(u,v) if l < d[v]: d[v] = l pi[v] = u def dag(graph,s): l = topSort(graph) d,pi = {},{} for v in graph.vertices(): d[v] = float('inf') pi[v] = None d[s] = 0 for u in l: for v in graph.getVertices(u): dag_relax(d,pi,graph,u,v) return d,pi |
Dijkstra算法
1) 将所有图顶点\(x\)按\(x.d\)建为最小优先队列\(Q\);
2) 出队顶点\(u\)并松弛化\(u\)的所有出边,并用\(decrease\)维护顶点排序符合优先队列性质;
3) 循环上述步骤直到\(Q\)为空,此时节点记录了最短路径树与最短路值;
Dijkstra算法属于贪心策略,其代价优于Bellman-Ford算法,但不允许图中存在非负权边。无负权边意味着对任意路径而言,若在其上加一条边,那么新路径总权重不可能更小。该算法较符合直觉,可通过反证法形式化的证明:
1) 计已出队顶点集为\(S\)。假设\(u\)是第一个即将出队但此时不满足\(u.d = \delta(s,u)\)的顶点;
2) 排除即将首次出队(源点出队)的情况,因为任何时刻\(s.d = \delta(s,s) = 0\);
3) 排除从源点不可到达即将出队顶点的情况,因为任何时刻\(u.d = \delta(s,u) = \infty\);
4) 综合(1)(2)可以设至少存在一条\(s\)到\(u(u\neq s)\)的最短路径\(p\)(至少含两个顶点),故\(u\)即将出队前\(p\)是从\(S\)(即\(s\))到\(V – S\)(即\(u\))的,此时刻计\(y\)(允许\(y=u\))为\(p\)中排最前的\(V-S\)元素,\(x \in S\)(允许\(x=s\))为\(p\)中\(y\)的前驱;
5) 断言\(u\)即将出队时\(y.d = \delta(s,y)\)。因为\(x\)先于\(u\)出队(\(x\)先在\(S\)中),由(1)的假设\(x\)即将出队时和这之后有\(x.d=\delta(s,x)\),\(x\)出队后松弛\((x,y)\)边,根据引理(4)有\(y.d = \delta(s,y)\),所以\(u\)即将出队时的断言成立;
6) 在\(p\)中\(y\)于\(u\)之前(或\(u=y\)),故\(u.d \geq \delta(s,u) \geq \delta(s,y)\),根据(5)可知在\(u\)即将出队时\(\delta(s,y) = y.d \),\(u\)此时为队头,\(y\)此时也位于队列(或\(u=y\)),故\(y.d\geq u.d\)。结合上述讨论,此时\(u.d = \delta(s,u) = \delta(s,y) = y.d\)与(1)矛盾;
综上所述\(Q\)中的每个顶点\(v\)在即将出队时都有\(\delta(s,v)=v.d\),故Dijkstra算法是正确的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 | class Graph: def __init__(self): self.d = dict() def addVertex(self,i): self.d[i] = dict() def addEdge(self,i1,i2,w): self.d[i1][i2] = w def getWeight(self,i1,i2): return self.d[i1][i2] def setWeight(self,i1,i2,w): self.addEdge(i1,i2,w) def getVertices(self,i): return self.d[i].keys() def vertices(self): return self.d.keys() class MinHeap: @staticmethod def parent(i):return 0 if i==0 else (i//2-1 if i%2==0 else i//2) @staticmethod def left(idx):return 2 * idx + 1 @staticmethod def right(idx):return 2 * idx + 2 def _heapify(self, idx, lastIdx): arr = self.arr keys = self.keys indexs = self.indexs l = self.left(idx) r = self.right(idx) x = idx if l <= lastIdx and keys[arr[l]] < keys[arr[idx]]: x = l if r <= lastIdx and keys[arr[r]] < keys[arr[x]]: x = r if x != idx: arr[x], arr[idx] = arr[idx], arr[x] indexs[arr[x]], indexs[arr[idx]] = indexs[arr[idx]], indexs[arr[x]] self._heapify(x,lastIdx) # 数组lst存放元组( 优先级值(key), 对象 ) def __init__(self,lst): self.arr = [] self.keys = {} self.indexs = {} for tp in lst: self.arr.append(tp[1]) self.indexs[tp[1]] = len(self.arr)-1 self.keys[tp[1]] = tp[0] def contain(self,k): return self.keys.get(k)!=None def pop(self): arr = self.arr keys = self.keys indexs = self.indexs if len(arr) == 0: return None if len(arr) == 1: k = arr.pop() keys.pop(k) indexs.pop(k) return k last = len(arr) - 1 arr[last], arr[0] = arr[0], arr[last] indexs[arr[last]], indexs[arr[0]] = indexs[arr[0]], indexs[arr[last]] self._heapify(0,len(arr)-2) k = arr.pop() keys.pop(k) indexs.pop(k) return k # 把堆中的对象k的优先级降为key并维持堆性质 def decrease(self,k,key): arr = self.arr keys = self.keys indexs = self.indexs i = self.indexs[k] keys[arr[i]] = key p = self.parent(i) while i > 0 and keys[arr[p]] > keys[arr[i]]: arr[i], arr[p] = arr[p], arr[i] indexs[arr[i]], indexs[arr[p]] = indexs[arr[p]], indexs[arr[i]] i = p p = self.parent(i) def dijkstra_relax(d,pi,graph,heap,u,v): l = d[u] + graph.getWeight(u,v) if l < d[v]: if heap.contain(v): heap.decrease(v,l) d[v] = l pi[v] = u def dijkstra(graph,s): d,pi = {},{} for v in graph.vertices(): if v!=s: d[v] = float('inf') pi[v] = None heap = [(v,k) for k,v in d.items()] d[s] = 0 heap.insert(0,(0,s)) heap = MinHeap(heap) while len(heap.arr)>0: u = heap.pop() for v in graph.getVertices(u): dijkstra_relax(d,pi,graph,heap,u,v) return d,pi |