哈夫曼编码

字符编码

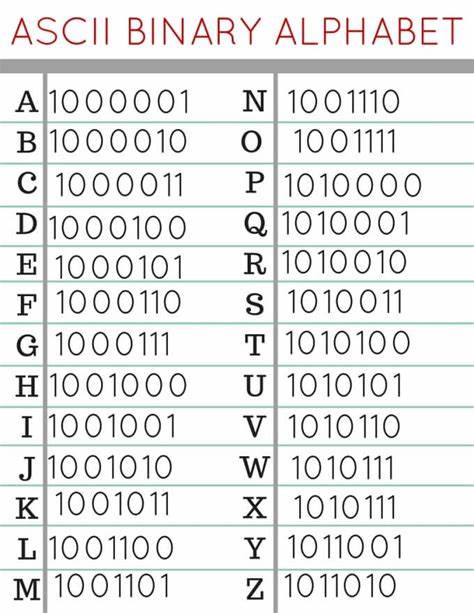
编码指把相同信息在不同的形式间转化，例如把图片储存为像素(x,y,r,g,b)，把直角坐标方程改写为极坐标方程，把26个字母用26个二进制数表示，把明文转为密码和密文等等。无论信息形式如何变化，它们依然是同样的信息。字符编码研究如何用二进制形式表示某种语言的字符，其可被分类为定长编码与变长编码。基础ASCII码是种定长编码，无论是英文逗号、空格、回车、换行甚至响铃都有自己的ASCII码。其定长策略是在所有二进制数(编码)前补0，保证每个编码都是7-Bit。强国官方编码GB18030是种变长编码，其有1/2/4字节三种长度，1字节长度的是ASCII的超集，2字节长度的是GBK的超集，4字节长度的是其他新加入的生僻的中文字符与中文符号。

前缀编码

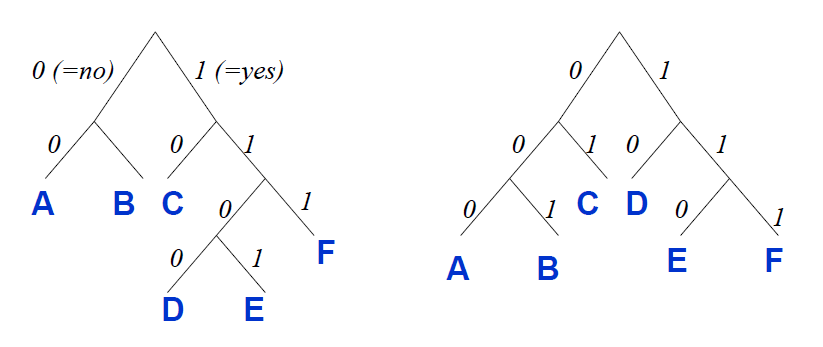
对任意字符串的任意前缀编码方案，每个字符的编码都不是其他编码的前缀。任何前缀编码方案都可用二叉树(如上图)表示，其非叶节点的左/右边表示0/1，从根节点出发可根据编码方案“生成”编码树。由于前缀码间互不为前缀，故字符不会出现在非叶节点，故叶节点必为被编码字符本身。对字符串\(S\)与其前缀编码二叉树\(T\)，设\(f(c)\)为字符\(c\)的出现次数，\(d(c)\)为字符\(c\)在前缀编码二叉树的深度，编码二叉树所对应的代价为\(B(T)=\sum f(c)d(c)\)，然后研究如何找到最低代价(最优压缩率)的前缀编码方案。首先给出一些有用的引理：

1) 任意字符串都存在能达到其最优压缩率的前缀编码方案；

2) 最优压缩率的前缀编码二叉树必为满二叉树(所有节点出度都不等于1)；

证明：若存在\(x\)只有单孩子\(y\)，用\(y\)顶替\(x\)的位置可使\(y\)子树上所有叶节点的编码位数下降。

3) 将任意满二叉树的叶节点数目计为\(z\)，则其非叶节点数目为\(z-1\)；

证明：将任意非空二叉树的2/1/0出度节点数计为\(x\)/\(y\)/\(z\)。利用边数与节点数可建立等式\(x+y+z=2x+y+1\)，所以有\(z=x+1\)。对于满二叉树恒有\(y=0\)，所以非叶节点数为\(x=z-1\)。

利用上述引理，求字符串的最优编码的问题可以转化为求非空的满二叉树问题。

哈夫曼编码

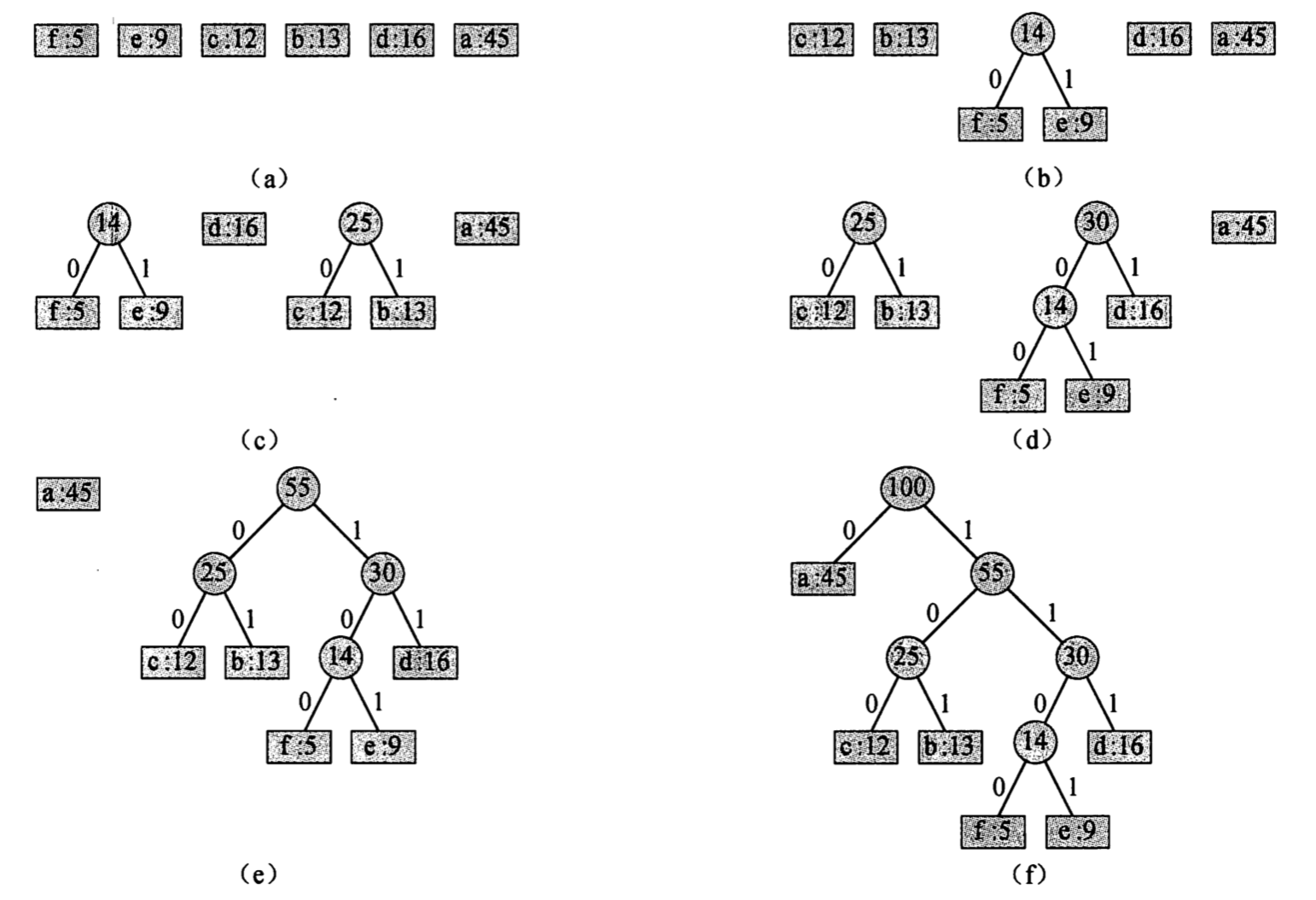
哈夫曼编码是求字符串最优前缀编码的算法，编码方案对应的二叉树称为哈夫曼树。在讨论算法前给出引理：

1) 设\(x,y(x\leq y)\)为字符串\(S\)中出现次数最少的其中2个字符，那么\(S\)必然存在某个最优前缀编码树\(T\)，在\(T\)中\(x\)与\(y\)为兄弟叶节点(\(x\)与\(y\)的编码的位数相等且仅仅在最末位不等)；

证明：设\(a,b(a\leq b)\)为\(T\)深度最大非叶节点的双叶节点，则\(f(x) \leq f(a),f(y) \leq f(b)\)，注意不同字母可能指代同个节点。交换\(a,x\)位置可得树\(T’\)，代价差\(B(T)-B(T’)=f(x)d_T(x)+f(a)d_T(a)-f(x)d_T(a)-f(a)d_T(x)\)，进一步整理得\(B(T)-B(T’)=(f(a)-f(x))(d_T(a)-d_T(x)) \geq 0\)。同理可交换\(T’\)中\(b\)与\(y\)得到编码树\(T’’\)满足\(B(T’)-B(T’’) \geq 0\)。由于\(T\)最优故\(T’’\)必为最优。

2) 设\(x,y(x\leq y)\)为字符串\(S\)中出现次数最少的其中2个字符，用\(S\)不包含的字符\(z\)替换\(x\)与\(y\)得到新的字符串\(S’\)。设\(T’\)为\(S’\)的最优编码二叉树，若将\(T’\)中\(z\)对应叶节点新增左右孩子\(x\)与\(y\)得到新树\(T\)，则\(T\)为\(S\)的其中一个最优树；

证明：首先考虑把\(B(T)\)用\(B(T’)\)来表示，\(f(x)d_T(x)+f(y)d_T(y)=(f(x)+f(y))(1+d_{T’}(z))\)。由于两树的其他部分相同，故\(B(T)=B(T’)+f(x)+f(y)\)。假设\(T\)非\(S\)的最优树，根据上述引理设\(T’’\)为\(S\)的最优树且\(x\)与\(y\)为\(T’’\)的一对兄弟叶节点。同理用\(z\)替换\(x\)与\(y\)的父节点得到\(T’’’\)则\(B(T’’’)=B(T’’)-f(x)-f(y)\)。整理上述结果可得\(B(T’’’)=B(T’’)-f(x)-f(y)<B(T)-f(x)-f(y)=B(T’)\)。由于\(T’\)为最优树，故假设不成立。

利用上述引理可以给出如下的算法流程：

1) 遍历整理字符串\(S\)为编码二叉树的节点，约定\(node.c\)为字符，\(node.f\)为字符在字符串的出现次数；

2) 将上述节点放入按\(node.f\)排序的最小优先队列\(Q\)；

3) 从\(Q\)出队2个节点计为\(a\)与\(b\)，将其作为新节点\(x\)的左右子树，并令\(x.f=a.f+b.f\)，最后将\(x\)入队\(Q\)。持续的循环该步骤，直到\(Q\)中仅剩下1个节点，此时算法结束，该节点即哈夫曼树树根；

在使用二叉堆实现的优先队列时，该算法的时间复杂度显然是\(O(nlgn)\)，其具体实现如下。该实现使用Python提供的堆(heapq)模块。对于二叉树节点(Node)，code属性是与节点一一映射的入边代表的二进制值。