活动选择问题

活动选择问题

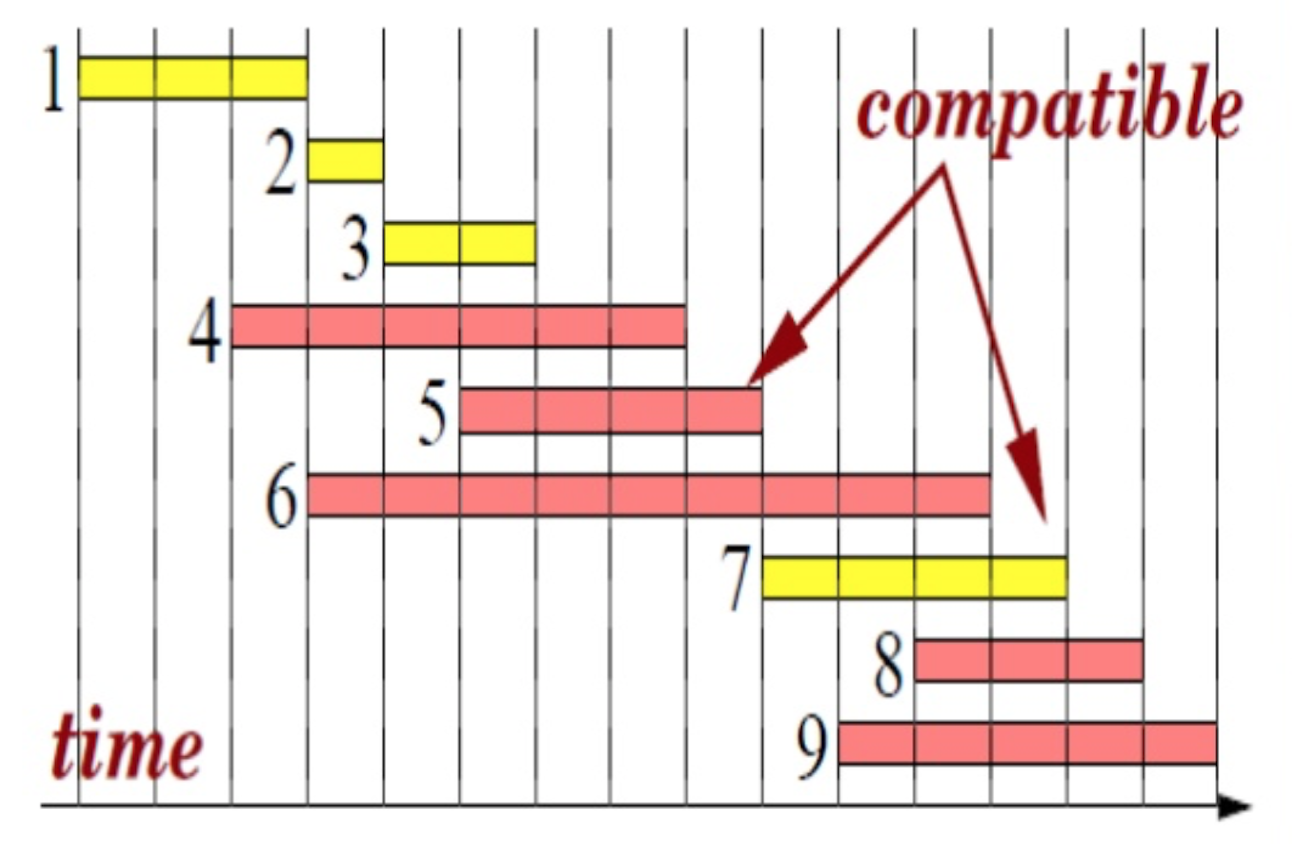
问题可表述为“设\(S[0,1…n]\)为‘活动’的序列，每个‘活动’有开始、结束时间，\(S\)已按结束时间升序排序。规定所有‘活动’独占同一个教室，求出\(S\)中的‘活动’最多能安排多少个”。上图是其中一种\(S\)的例子。

设\(L\)是一个最优活动安排序列(已排序)。任取\(L[k]\)，并用其划分序列\(L_1 = L[0,…,k-1],L_2=L[k+1,…]\)。然后设\(s_1\)是“\(L[k]\)开始前结束的\(S\)中的所有活动”，\(s_2\)是“\(L[k]\)结束后开始的\(S\)中的所有活动”。可发现如果把\(s_1,s_2\)作为原问题的输入，则\(L_1,L_2\)必可分别作为最优活动安排序列，否则\(L\)本身就不是原问题的最优解了。然后任取\(L_1[k_1]\)……可以发现上述结论是递归的。然后用这个性质去找最优解，先回到原问题上，其任意最优活动安排序列都符合“空序列,包含\(S[0]\),包含\(S[1]\),包含\(S[2]\)…”中的至少一种，如果符合的是空序列，那么解就是0，否则就遍历这些元素，设每次遍历到的元素是\(x\)，然后用其划分\(S\)为“\(x\)开始前结束的\(S\)中的所有活动”，“\(x\)结束后开始的\(S\)中的所有活动”这两个序列，然后分别递归的求出它们的解并计做\(c_1,c_2\)，然后求出\(c=c_1+1+c_2\)，即放入\(x\)后的总活动数。每次遍历都会求一次\(c\)，其中最大的那个就是解。

然后考虑将上述讨论转化为动态规划算法。设\(S_{ij}\)为“\(L[i]\)结束后开始，\(L[j]\)开始前结束的所有活动，且已按结束时间升序排序”，\(c_{ij}\)为“以\(S_{ij}\)为输入时上述问题的解”。这里子问题和原问题好像还没有直接关联，这里假想在\(S\)前面加一个结束时间为\(S[0]\)开始时间的元素，在\(S[n]\)后面加一个开始时间为\(S[n]\)结束时间的元素，那么原问题的解就能变成\(c_{0,(n+2)}\)。接着就是最重要的状态转移方程\(c_{ij}=max\{ c_{ik}+1+c_{kj} | k\in [i,j] \}\)，边界情况是\(i\geq j\)时\(c_{ij}=0\)。

构造数组\(c[i][j]\)时，先全填0，只用计算\(i<j\)的情况，但还是需要\(n^2\)时间。计算时按\(i,j\)递增顺序就能保证需要子问题的解时其都已在数组中。由于每计算一个数组项都需要额外的遍历，遍历的元素数和\(n\)同阶，故时间复杂度是\(O(n^3)\)。

按\(i,j\)自然递增的顺序构造就能保证子问题的解都已经在数组中，但每次求值都需要便利\(j – i\)次，

那么\(S\)中满足“\(l[k]\)开始前结束的所有活动”

那么把这个方案中的活动划为左右

先找DP算法，设\(S_{ij}\)为“\(L[i]\)结束后开始，\(L[j]\)开始前结束的所有活动，且已按结束时间升序排序”，\(c_{ij}\)为“以\(S_{ij}\)为输入时上述问题的解”。其状态转移方程是“\(S_{ij}\)非空时\(c_{ij}=max\{ c_{ik}+1+c_{kj} | k\in [i,j] \}\)，否则\(c_{ij}=0\)”。

设\(c_{ij}\)为“设\(L’\)是\(L[i]\)结束后，\(L[j]\)开始前的所有活动构成的\(L\)的子序列，以\(L’\)为输入时上述问题的解”。这里先给出其满足状态转移方程\(c_{ij}=max\{ c_{ik}+1+c_{kj} | k\in [i,j] \}\)。

设子问题的解\(S_{ij}\)为“满足\(L[i]\)结束时间后，\(L[j]\)开始时间前的活动子序列”，

然后分析该问题的最优子结构。设\(S_{ij}\)为“\(L[i]\)结束时间后且\(L[j]\)开始时间前”的所有活动，\(c_{ij}\)为“\(S_{ij}\)所对应的子问题的解的元素数”。若存在包含\(L[k]\)的\(c_{ij}\)对应的原问题的解，则\( c_{ij}=c_{ik}+1+c_{kj}\)。此处难以确定是否包含\(L[k]\)，可通过遍历得出\(c_{ij}=max\{ c_{ik}+1+c_{kj} | i\leq k \leq j \}\)。这样就得出了状态转移方程，可通过DP求解该问题。由于有状态转移方程有两个自变量，并且每次求值需要一次遍历，故其时间复杂度为\(O(n^3)\)。然后刻画问题的最优子结构，设\(S_{ij}\)子问题的某个解包含\(L[k]\)，那么\(S_{ik}\)子问题的解、\(L[k]\)、\(S_{kj}\)子问题的解必可构成\(S_{ij}\)子问题的解。

接下来考虑找出优于DP的策略，换用记号\(S_k\)表示开始时间在\(L[k]\)结束时间后的所有活动，\(L[m]\)为\(S_k\)中最早结束的活动，那么\(L[m]\)必存在于\(S_k\)对应子问题的某个解中，因为\(L[m]\)必然可以替换掉\(S_k\)所有解中最早结束的活动，替换后的解同样可作为解。然后进一步得出该新记号下的最优子结构，若活动\(L[m]\)为\(S_k\)中最早结束的活动，那么\(L[m]\)与\(S_m\)子问题的某个解可构成\(S_k\)的解。根据该最优子结构，若从左到右遍历按结束时间升序的\(L\)，若当前元素的开始时间大于上次选择元素的结束时间，则选择当前元素。最终选择的元素构成原问题的一个解。