B树

B树(B-Tree)

1970年德国学者R.Bayer提出B树，这是一种多路的自平衡树，其相比于红黑树等自平衡二叉树并没有更好的渐进代价，但在一些场景中其实际性能优于自平衡二叉树。B树包含一个称为最小度数(degree)的关键参数，该参数可以是大于1的任意整数，初始化B树时需同时给定该参数，之后该参数固定不变。最小度数为\(t\)的B树可通过如下几点来定义：

1) B树节点可包含多个关键字，非树根节点的关键字数目的取值范围是\([t-1,2t-1]\)，树根节点是\([0,2t-1]\)，树根节点的关键字数目等于0当且仅当B树中无关键字，关键字数目等于\(2t-1\)的节点被称为满节点。节点的关键字被非严格递增排序，任意节点\(x\)的第\(i\geq 0\)个关键字可计为\(x.keys[i]\)。需明确任何时刻都能得到任意节点\(x\)此时的关键字数目；

2) B树节点可包含多个孩子指针，叶节点无孩子指针，非叶节点有“关键字数目+1”个孩子指针且它们都不为空。节点的孩子指针有序，任意非叶节点\(x\)的第\(i\geq 0\)个孩子可计为\(x.children[i]\)，对于该节点任意第\(j\)个关键字\(x.keys[j]\)，\(x.children[j]\)子树中的任意关键字都小于等于\(x.keys[j]\)，\(x.children[j+1]\)子树中的任意关键字都大于等于\(x.keys[j]\)。需明确任何时刻都能得到任意节点此时的孩子指针数目，为了方便可在节点中额外维护一个布尔值表示其是否为叶节点；

3) 任何B树都有非空的树根节点。不包含关键字的B树被称为空树，其仅有1个不包含关键字的叶子节点；

4) 同一个B树中的所有叶节点高度相等；

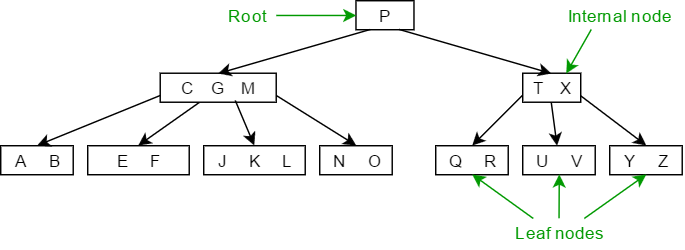
可发现B树的定义较为繁琐，一般会大致按照上图的方式绘制B树，其中的大写字母表示关键字。本文对B树运算的定义和前文对BST运算的定义一致，只需实现按单个\(key\)的查找、插入、删除。但要额外保证每次运算前后整个树符合B树的定义，且运算代价和BST运算一样要以树高为上界，否则构造B树就失去意义。下述性质将保证B树属于自平衡树：

a1) 对于包含\(n\geq 1\)个关键字的最小度数为\(t\)的B树，其高度至多取到\(\log_t(\frac{n+1}{2})+1\)；

证明：显然让每层的关键字数目都取最小值能最大化树高度，第1层有1个节点且该节点中至少有1个关键字，第2层至少有2个节点且每个节点中至少有\(t-1\)个关键字，第3层至少有\(2t\)个节点且每个节点中至少有\(t-1\)个关键字，第4层至少有\(2t^2\)个节点且每个节点中至少有\(t-1\)个关键字……所以有\(n\geq 1+(t-1)\sum_{i=1}^{h-1}{2^{t-1}}=1+2(t-1)(\frac{t^{h-1}-1}{t-1})=2t^{h-1}-1\)，其中\(h\)是B树的高度，整理该不等式后两边取对数可得到\(h\leq \log_t(\frac{n+1}{2})+1\)。

B树与红黑树的对应关系

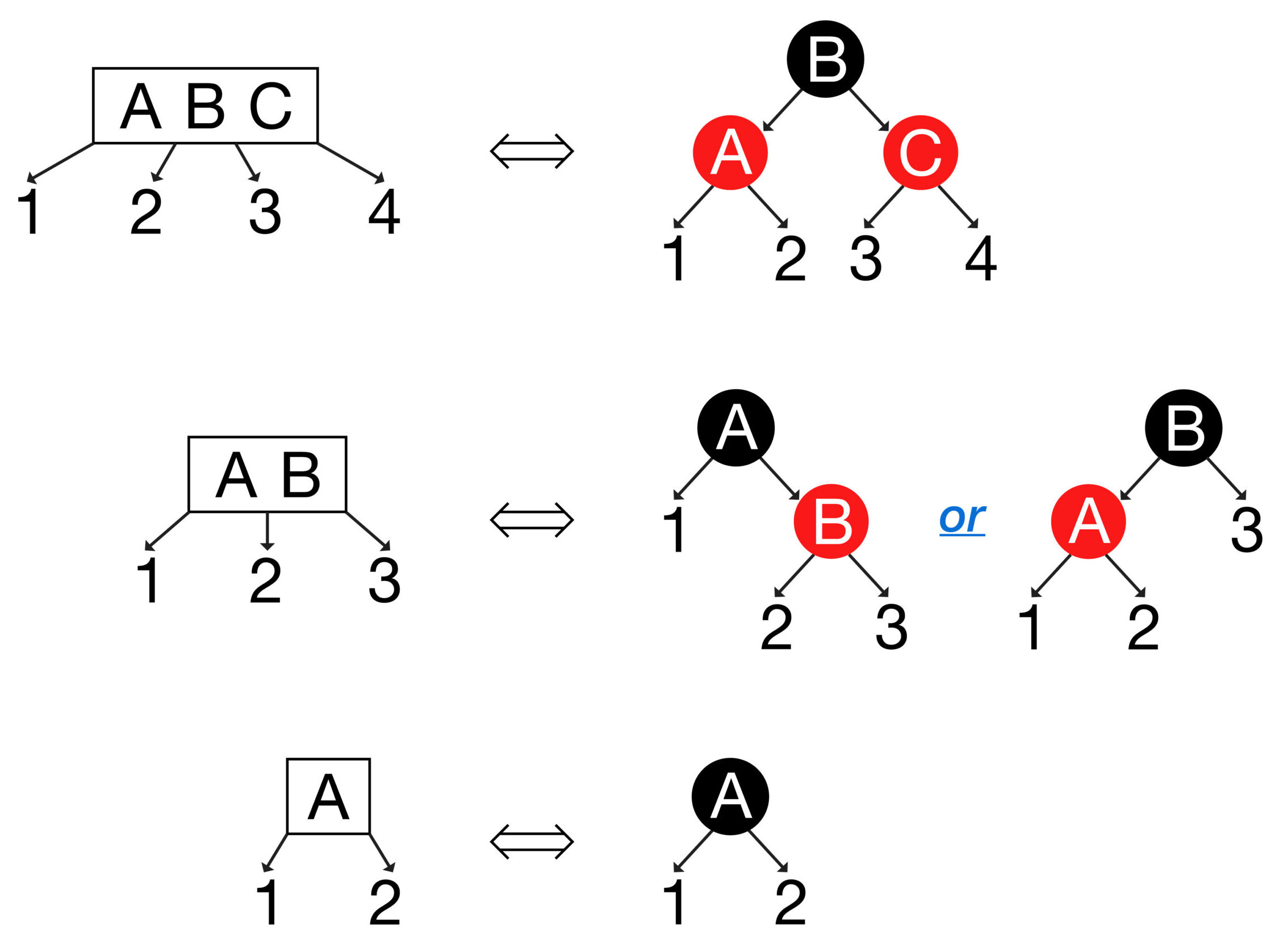
历史上红黑树是在B树的基础上提出的，任何红黑树都能转化为与之等价的\(t=2\)的B树。为详细描述这种转化步骤，先构造递归操作\(f(x)\)，其用于创建并返回与红黑树的黑树根子树或空子树\(x\)等价的B树子树，\(f(x)\)的步骤分情况如下：

1) \(x\)为空：直接返回空即可；

2) \(x\)非空且有2个红孩子：可参考上图第1行。先根据上述A,B,C创建包含3个关键字的B树节点\(x\)，然后对上述1,2,3,4指针依次递归执行\(f\)，并且将递归所返回的4个B树子树按顺序接到\(x\)的4个孩子指针上，最后返回\(x\)即可；

3) \(x\)非空且有1个红孩子：可参考上图第2行。先根据上述A,B创建包含2个关键字的B树节点\(x\)，然后对上述1,2,3指针依次递归执行\(f\)，并且将递归所返回的3个B树子树按顺序接到\(x\)的3个孩子指针上，最后返回\(x\)即可；

4) \(x\)非空且无红孩子：可参考上图第3行。先根据上述A创建包含1个关键字的B树节点\(x\)，然后对上述1,2指针依次递归执行\(f\)，并且将递归所返回的2个B树子树按顺序接到\(x\)的2个孩子指针上，最后返回\(x\)即可；

这里分析上述步骤的正确性，根据红黑树定义和上述对不同情况的划分，若\(x\)为空则\(x\)的黑高等于0，\(f(x)\)不会创建B树节点也不执行子递归，若\(x\)为黑节点则\(x\)的黑高大于0，\(f(x)\)会创建1个B树节点并执行子递归，这些子递归都作用于黑节点或空节点，这些节点的黑高都为\(x\)的黑高-1。这说明若\(x\)是黑树根的子树或空子树，\(f(x)\)能创建高度等于\(x\)的黑高的B树子树。

根据\(f\)可得到将红黑树转化为B树的步骤，由于红黑树树根是黑节点或空节点，对其执行\(f\)即得到与之等价的B树树根。需注意到若红黑树为空则\(f\)会返回空，由于B树不允许树根为空节点，该情况需手动创建1个不含关键字的节点作为B树树根。同理\(t=2\)的B树也能转化为与之等价的红黑树，但包含2个关键字的B树节点对应2种转化后的形态(可参考上图第2行)，所以虽然任何红黑树都能按上述步骤映射为一个\(t=2\)的B树，但\(t=2\)的B树不保证能按类似的方式映射为一个红黑树。

B树的分裂与合并

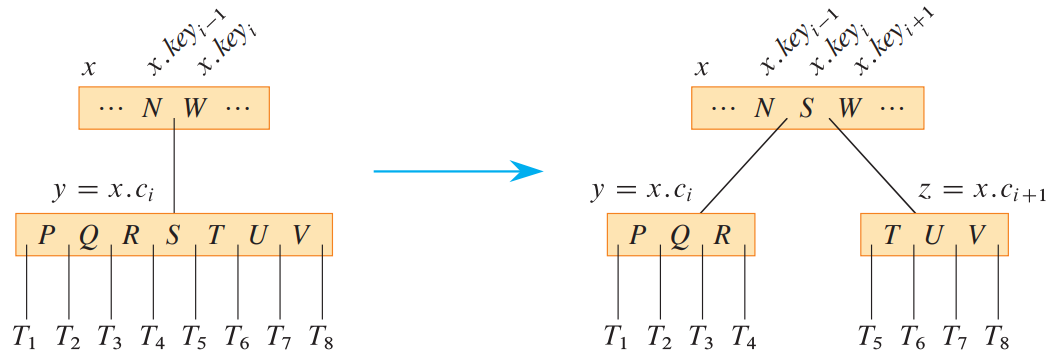
B树的插入运算包含被称为分裂(split)的步骤，这里用\(splitChild(x, i)\)操作实现该步骤。\(splitChild(x, i)\)的功能是按上图的方式拆分节点\(x.children[i]\)，并且执行前后都要符合B树定义。于是执行前\(x.children[i]\)的关键字数目必须为\(2t-1\)，并且必须从最中间的关键字分裂(由于\(2t-1\)是奇数所以最中间无歧义)，只有这样才能使分裂得到的2个节点的关键字数目都不低于\(t-1\)。在具体实现时通常复用\(x.children[i]\)本身作为分裂得到的左节点，这样更方便并且只需创建右节点。

B树的删除运算包含被称为合并(merge)的步骤，这里用\(mergeChild(x, i)\)操作实现该步骤。\(mergeChild(x, i)\)的功能是按上图的逆过程合并节点\(x.children[i]\)与其右兄弟\(x.children[i+1]\)，并且执行前后都要符合B树定义。于是执行前这2个节点的关键字数目必须都为\(t-1\)，只有这样才能使合并得到的节点的关键字数目不高于\(2t-1\)。在具体实现时通常复用\(x.children[i]\)本身作为合并得到的节点，这样更方便并且无需创建新节点。

B树的旋转

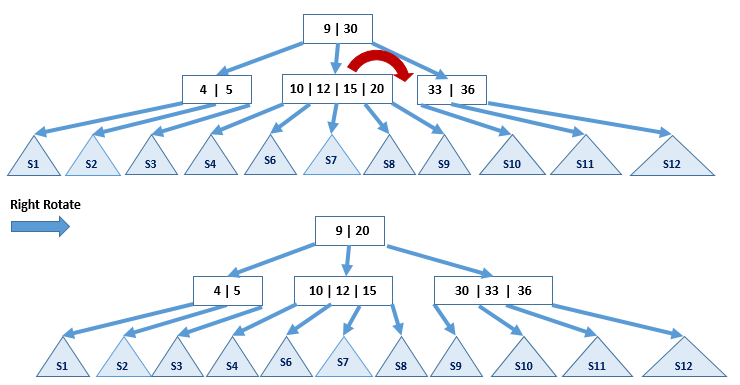
B树的删除运算包含这里称为左旋转和右旋转的步骤，这里用\(rightRotate(x, i)\)和\(leftRotate(x, i)\)操作实现该步骤，需明确大部分教材都不将这种操作称为旋转。\(rightRotate(x, i)\)的功能是按上图的方式使\(x.children[i-1]\)的关键字数目和孩子指针数目-1，\(x.children[i]\)的关键字数目和孩子指针数目+1，并且执行前后都要符合B树定义。于是执行前\(x.children[i-1]\)的关键字数目必须大于\(t-1\)，\(x.children[i]\)的关键字数目必须小于\(2t-1\)。\(leftRotate(x, i)\)的功能则是使\(x.children[i+1]\)的关键字数目和孩子指针数目-1，\(x.children[i]\)的关键字数目和孩子指针数目+1，并且执行前后都要符合B树定义。

B树的查找运算

首先定义\(firstKeyGeqTo(x, k)\)操作用于得到\(x.keys\)中首个不小于\(k\)的元素的下标，若不存在这种元素则返回-1。该操作是查找、插入、删除的公共步骤。顺序查找(sequential search)是该操作的基本实现，其代价是节点关键字数目，步骤是顺序遍历所有元素，若某轮遍历首次发现符合要求的元素则返回其下标，否则返回-1。二分查找(binary search)是该操作的更优实现，其代价是节点关键字数目的对数，但由于\(t\)可看作常数，故使用顺序查找或二分查找并不影响B树运算的渐进代价。

考虑构造递归操作\(find(x, k)\)用于在\(x\)节子树中查找关键字\(k\)。其步骤分情况如下：

1) \(x\)是叶节点：置\(i=firstKeyGeqTo(x, k)\)。若\(i\geq 0\)且\(x.keys[i]=k\)则返回\(x\)表示查找成功，否则返回空表示失败；

2) \(x\)不是叶节点：置\(i=firstKeyGeqTo(x, k)\)。若\(i\geq 0\)且\(x.keys[i]=k\)则返回\(x\)表示查找成功。若\(i\geq 0\)且\(x.keys[i]<k\)则返回\(find(x.children[i],k)\)。若\(i<0\)则置\(j\)为此时\(x.children[i]\)的关键字数目，返回\(find(x.children[j],k)\)；

最后完整实现B树的查找运算。只需对B树的树根\(r\)执行并返回\(find(r, k)\)即可。其代价上界是B树高度。

B树的插入运算

根据B树的定义，任何关键字\(k\)都能被放入某个叶节点的合适位置，且放入后不违反除节点关键字数目上限外的其他B树定义。假设此时已将关键字\(k\)放入叶节点\(x\)的合适位置，若\(x\)的关键字数目不大于\(2t-1\)则此时符合B树定义，否则需分裂\(x\)，若分裂后\(x\)的父亲关键字数目大于\(2t-1\)，需继续分裂\(x\)的父亲……最后如果树根被分裂，需将分裂出来的关键字作为新树根。

上面已给出插入运算的核心思路，但在实现该运算时，通常并不希望算法包含向父亲节点回溯的步骤，所以需要进一步调整上述思路，使得算法在每次跳转至选定的下一层的节点前就预先执行好分裂操作，于是算法在每次到达一个节点时，该节点的关键字数目就已经小于\(2t-1\)，最终在算法到达叶节点时，可直接插入关键字并且无需检查关键字数目。

考虑构造递归操作\(insert(x, k)\)用于在\(x\)子树插入1个关键字\(k\)，要求执行前\(x\)的关键字数目小于\(2t-1\)。其步骤分情况如下：

1) \(x\)是叶节点：置\(i=firstKeyGeqTo(x, k)\)。若\(i\geq 0\)则在\(x.keys[i]\)前面放入\(k\)，否则在\(x.keys\)尾部追加\(k\)。最后返回\(x\)；

2) \(x\)不是叶节点：置\(i=firstKeyGeqTo(x, k)\)。然后继续分情况进行讨论：

2.1) \(i\geq 0\)：若\(x.children[i]\)的关键字数目小于\(2t-1\)则返回\(insert(x.children[i], k)\)，否则\(splitChild(x, i)\)，此时原\(x.children[i]\)被分裂，若\(k\leq x.keys[i]\)则返回\(insert(x.children[i], k)\)，否则返回\(insert(x.children[i+1], k)\)；

2.2) \(i<0\)：置\(j\)为\(x.children[i]\)的关键字数目。若\(j<2t-1\)则返回\(insert(x.children[j], k)\)，否则\(splitChild(x, j)\)，此时原\(x.children[j]\)被分裂，若\(k\leq x.keys[j]\)则返回\(insert(x.children[j], k)\)，否则返回\(insert(x.children[j+1], k)\)；

最后完整实现B树的插入运算。若B树树根\(r\)的关键字数目小于\(2t-1\)则执行并返回\(insert(r,k)\)，否则创建新树根\(p\)并将\(r\)作为\(p\)的孩子，然后执行\(splitChild(p, 0)\)，此时\(p\)只有1个关键字，执行并返回\(insert(p,k)\)。其代价上界是B树高度。

B树的删除运算

假设此时已经从B树的叶节点\(x\)去掉1个关键字，若\(x\)的关键字数目不小于\(t-1\)，则符合B树定义。否则若\(x\)有左兄弟或右兄弟\(y\)且\(y\)的关键字数目大于\(t-1\)，可通过右旋转或左旋转使\(x\)的关键字数目+1，进而符合B树的定义。否则合并\(x\)与\(x\)的左或右兄弟，合并得到的节点的关键字数目一定符合B树定义，但该次合并使其父亲\(p\)失去1个关键字，若此时\(p\)的关键字数目不小于\(t-1\)……最后如果原本只有一个关键字的树根在合并后失去关键字，那么需要将该次合并所得到的节点作为新的树根。

假设需要从B树的非叶节点\(x\)去掉\(x.keys[i]\)关键字。根据B树的定义，从\(x.children[i]\)出发沿着每个节点的最右孩子指针可到达叶节点\(y\)，\(y\)的最末关键字\(y.keys[j]\)即是\(x.keys[i]\)的“中序前驱关键字”。此时如果置\(x.keys[i]=y.keys[j]\)，接下来的问题就是如何从叶节点\(y\)中去掉\(y.keys[j]\)，于是就大致能按照上述的从叶节点删除关键字的思路解决。

上面已经给出了删除运算的核心思路，但在实现该运算时，通常并不希望算法包含向父亲节点回溯的步骤，所以需要进一步调整上述思路，使得算法在每次跳转至选定的下一层的节点前就预先执行好旋转或合并操作，于是算法在每次到达一个节点时，该节点的关键字数目就已经大于\(t-1\)(不包括树根)，最终在到达叶节点时，可直接去掉关键字并且无需检查关键字数目。

考虑构造递归操作\(remove(x, k)\)用于在\(x\)子树删除1个等于\(k\)的关键字，要求执行前\(x\)(不包括树根)的关键字数目大于\(t-1\)。其步骤分情况如下，其中操作\(removeNonLeaf(x, i)\)用于从非叶节点\(x\)去掉\(x.keys[i]\)，这里先不实现该操作：

1) \(x\)是叶节点：置\(i=firstKeyGeqTo(x, k)\)。若\(i\geq 0\)且\(x.keys[i]=k\)则去掉\(x.keys[i]\)并返回\(x\)，否则返回空；

2) \(x\)不是叶节点：置\(i=firstKeyGeqTo(x, k)\)。然后继续分情况进行讨论：

2.1) \(i\geq 0\)且\(k=x.keys[i]\)：说明要在非叶节点\(x\)中去掉关键字\(k\)，所以返回\(removeNonLeaf(x, i)\)；

2.2) \(i\geq 0\)且\(k<x.keys[i]\)：若\(x.children[i]\)的关键字数目大于\(t-1\)，返回\(remove(x.children[i], k)\)。否则若\(x\)有左兄弟并且其关键字数目大于\(t-1\)，执行\(rightRotate(x, i)\)，由于旋转后\(x.children[i]\)中原本的关键字和子树都不变，所以接下来也应该返回\(remove(x.children[i],k)\)。否则若\(x\)有右兄弟并且其关键字数目大于\(t-1\)，执行\(leftRotate(x, i)\)，然后同理也应该返回\(remove(x.children[i],k)\)。否则若\(i=0\)，执行\(mergeChild(x, i)\)，然后同理也应该返回\(remove(x.children[i],k)\)。否则执行\(mergeChild(x, i-1)\)，由于2个节点被合入\(x.children[i-1]\)，所以返回\(remove(x.children[i-1],k)\)；

2.3) \(i<0\)：置\(j\)为\(x\)的关键字数目。若\(x.children[j]\)的关键字数目大于\(t-1\)，返回\(remove(x.children[j], k)\)。否则若\(x\)有左兄弟并且其关键字数目大于\(t-1\)，执行\(rightRotate(x, i)\)，由于旋转后\(x.children[j]\)中原本的关键字和子树都不变，所以接下来也应该返回\(remove(x.children[j],k)\)。否则注意到\(x\)一定无右兄弟但一定有左兄弟，所以执行\(mergeChild(x, i-1)\)，由于2个节点被合入\(x.children[i-1]\)，所以返回\(remove(x.children[i-1],k)\)；

然后考虑实现\(removeNonLeaf\)，根据前面的思路首先应该下降至节点\(x.children[i]\)并保证其关键字数目大于\(t-1\)，但想要实现这一步会遇到点麻烦，假如\(x.children[i]\)的关键字数目等于\(t-1\)，则需要执行旋转或合并，这可能使\(x.keys[i]\)被下移到新位置\(x’.keys[i’]\)，如果这时继续下降至\(x.children[i]\)可能导致错误的结果，但好在该次旋转或合并不破坏B树性质，所以接下来应当跟踪到新位置\(x’.keys[i’]\)，若\(x’\)刚好是叶节点，直接去掉\(x’.keys[i’]\)就能完成\(removeNonLeaf\)操作，否则应继续下降至节点\(x’.children[i’]\)并保证其关键字数目大于\(t-1\)……为了方便描述，考虑构造递归操作\(descendTo(x, i)\)完成上述的下降步骤，其能够返回二元组\((x’,i’)\)满足执行后的\(x’.keys[i’]\)是执行前的\(x.keys[i]\)的位置，并且执行后要么\(x’\)是叶节点，要么\(x’\)是非叶节点且\(x’.children[i’]\)的关键字数目大于\(t-1\)。其具体步骤分情况如下：

1) \(x\)是叶节点：直接返回\((x,i)\)；

2) \(x\)不是叶节点：若\(x.children[i]\)的关键字数目大于\(t-1\)，则直接返回\((x,i)\)，否则需分情况讨论：

2.1) \(i>0\)且\(x.children[i-1]\)的关键字数目大于\(t-1\)：执行\(rightRotate(x, i)\)，此时原\(x.keys[i]\)的位置仍是\(x.keys[i]\)，并且\(x.children[i]\)的关键字数目已大于\(t-1\)，已经完成下降，故返回\((x,i)\)；

2.2) \(i\)小于\(x\)的关键字数目且\(x.children[i+1]\)的关键字数目大于\(t-1\)：执行\(leftRotate(x, i)\)，此时原\(x.keys[i]\)的位置变为\(x.children[i]\)的最末关键字\(x.children[i].keys[j]\)，需要继续下降，故返回\(descendTo(x.children[i],j)\)；

2.3) \(i>0\)且\(x.children[i-1]\)的关键字数目等于\(t-1\)：执行\(mergeChild(x, i-1)\)，此时原\(x.keys[i]\)的位置变为\(x.keys[i-1]\)，并且\(x.children[i-1]\)的关键字数目已大于\(t-1\)，已经完成下降，故返回\((x,i-1)\)；

2.4) \(i=0\)且\(x.children[i+1]\)的关键字数目等于\(t-1\)：执行\(mergeChild(x, i)\)，此时原\(x.keys[i]\)被移动为此时的\(x.children[i]\)的中间位置关键字\(x.children[i].keys[j]\)，需要继续下降，故返回\(descendTo(x.children[i],j)\)；

在确定好\(removeNonLeaf\)第一步的下降步骤后，接下来构造递归操作\(mostRight(x)\)来完成从\(x\)出发沿着每个节点的最右孩子指针下降至叶节点的步骤，其能够返回一个叶节点\(y\)，并确保\(y\)的关键字数目大于\(t-1\)，在执行前需要保证\(x\)(不包括树根)的关键字数目大于\(t-1\)。其具体步骤分情况如下：

1) \(x\)是叶节点：直接返回\(x\)；

2) \(x\)不是叶节点：置\(i\)为\(x\)的关键字数目，若\(i>t-1\)则直接返回\(mostRight(x.children[i])\)，否则需分情况讨论：

2.1) \(x.children[i-1]\)的关键字数目大于\(t-1\)：执行\(rightRotate(x, i)\)，返回\(mostRight(x.children[i])\)；

2.2) \(x.children[i-1]\)的关键字数目等于\(t-1\)：执行\(mergeChild(x, i-1)\)，返回\(mostRight(x.children[i-1])\)；

至此可完整得到\(removeNonLeaf(x, i)\)的步骤，首先置\(x’,i’ = descendTo(x, i)\)，若\(x’\)是叶节点，则去掉\(x’.keys[i’]\)并返回\(x’\)即可，否则置\(y=mostRight(x’)\)，置\(x’.keys[i’]\)为\(y\)的最末关键字，然后去掉\(y\)的最末关键字，最后返回\(y\)。

最后完整实现B树的删除运算。首先将B树树根计为\(r\)，然后置\(x=remove(r,k)\)。此时\(r\)中可能无关键字并且\(r\)不是叶节点，该情况不符合B树定义，所以遇到这种情况时需将\(r\)唯一的孩子作为B树的新树根。最后返回\(x\)。

总结与实现

实现B树节点时通常会将\(keys\)和\(children\)都实现为数组，这里还额外在节点中维护布尔值\(isLeaf\)来表示该节点是否为叶节点，叶节点的\(children\)指向空即可。最后给出B树的程序实现如下，其他未提到的细节见程序与注释。