二叉搜索树与二叉搜索树的平衡性

二叉搜索树(Binary Search Tree)

二叉搜索树也称二叉查找树、二叉排序树，简写为BST，是种基于二叉树的数据结构。下面给出其定义：

1) 二叉搜索树节点：额外包含一个关键字(\(key\))的二叉树节点；

2) 二叉搜索树：由二叉搜索树节点组成，要么是空树，要么左右子树都是二叉搜索树，并且若左子树非空，则左子树所有节点的\(key\)都不大于树根的\(key\)，若右子树非空，则右子树所有节点的\(key\)都不小于树根的\(key\)；

下面给出BST的关键性质，其也是另一种BST的等价定义，根据中序遍历的性质和BST的定义不难验证：

a1) 由BST节点构成的二叉树是BST \(\Leftrightarrow\) 该二叉树的中序序列按\(key\)非严格递增；

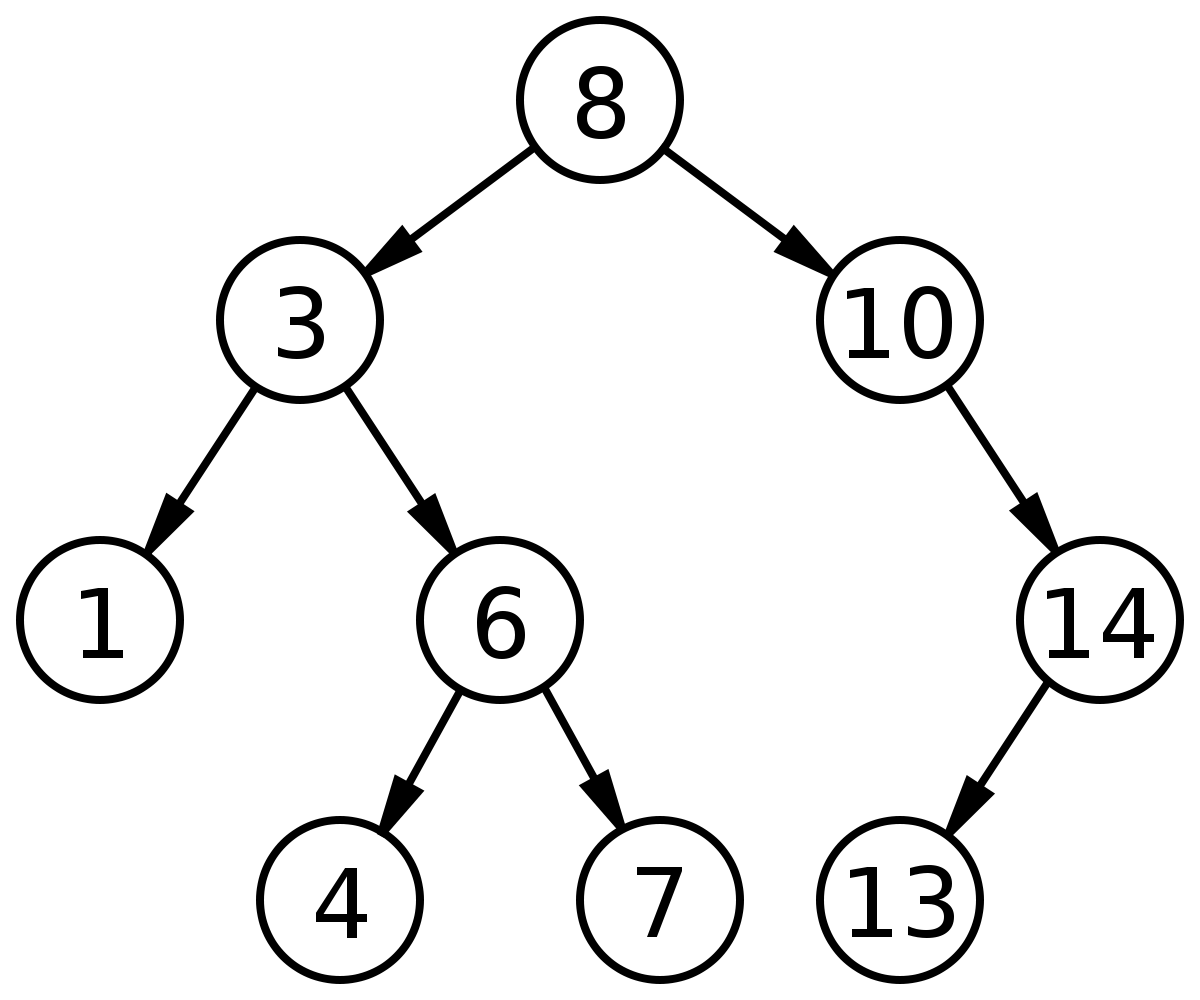
上图是BST的例子，绘制BST时会把\(key\)标注在节点上。BST本身的功能是存储一组\(key\)，并提供查找\(key\)、插入\(key\)、删除\(key\)的能力。本文约定BST允许存储多个重复\(key\)，因为这符合BST的定义，但也有部分场景或教材会要求\(key\)不允许重复。下面给出本文对BST运算的定义，其中的额外要求是为了方便之后的文章讨论其他基于BST的数据结构：

1) \(find(k)\)：查询是否存在至少一个\(k\)关键字。额外要求查询成功时返回其中一个关键字为\(k\)的节点，失败时返回空；

2) \(insert(k)\)：插入一个\(k\)关键字。额外要求返回BST新增的节点；

3) \(remove(k)\)：删除其中一个\(k\)关键字。额外要求删除成功时返回BST失去的节点，失败时返回假；

在上述定义的基础上，显然还需要保证每次运算前后的二叉树都符合BST定义。

二叉搜索树的运算

首先规定\(key\)是存储在节点中的数字变量，之后可用\(n.key\)表示节点\(n\)的\(key\)。然后额外要求所有节点存储一个\(parent\)指针表示其父亲，这能使BST运算更易实现一些，也能方便之后的文章讨论其他基于BST的结构，但这也使得每次运算前后都要额外保证所有节点的\(parent\)正确。下面讨论上述运算的步骤，由于其比较简单，故只给出核心思路与大致步骤：

1) \(find(k)\)：若树根为空则返回空。否则若\(k\)等于树根的\(key\)则返回树根。否则若\(k\)小于树根的\(key\)则\(key\)等于\(k\)的节点只可能在左子树，即等价于在左子树\(find(k)\)。否则\(key\)等于\(k\)的节点只可能在右子树，即等价于在右子树\(find(k)\)；

2) \(insert(k)\)：若树根为空则创建\(key\)为\(k\)的新树根并返回新树根。否则若\(k\)小于树根的\(key\)则只能将新节点插入左子树，等价于在左子树\(insert(k)\)。否则将新节点插入右子树(即规定等于时都插入到右子树)，等价于在右子树\(insert(k)\)；

3) \(remove(k)\)：先执行上述\(find(k)\)得到节点\(x\)，若\(x\)为空返回假，否则分情况处理如下：

3.1) \(x\)无孩子：若\(x.parent\)不存在则置树根为空。否则将\(x.parent\)的指向\(x\)的指针置空。最后返回\(x\)；

3.2) \(x\)有一个孩子：若\(x.parent\)不存在则置树根为该孩子，再将该孩子的\(parent\)置空。否则将\(x.parent\)的指向\(x\)的指针指向该孩子，再将该孩子的\(parent\)指向\(x.parent\)。最后返回\(x\)；

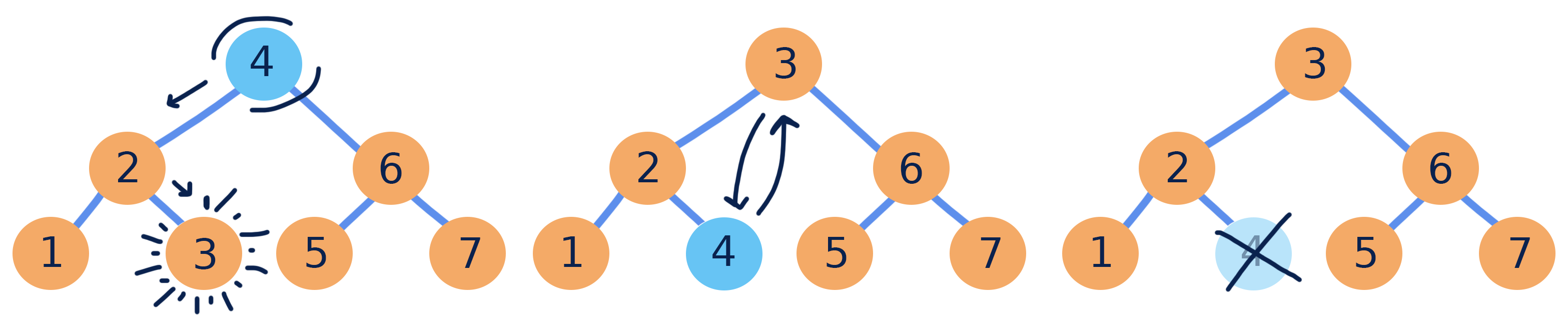
3.3) \(x\)有二个孩子：找到\(x\)左子树中的最右节点\(y\)(\(x\)的中序前驱)，根据二叉树性质\(y\)无右孩子，先按上述\(remove\)的前2种情况删掉\(y\)，此时\(y\)已经不在BST上，然后将\(x\)的\(key\)替换成\(y\)的\(key\)，最后返回\(y\)(该情况可参考上图)；

不难验证上述3种运算结束时的二叉树满足BST定义，并且对于其执行时所途径的节点，节点高度都是递减的，所以它们的代价上界都是BST的高度\(O(h)\)。另外上述\(find,insert\)虽然是递归给出的，但实现时应该转化为迭代步骤，这能保证\(O(1)\)的额外空间占用，考虑到它们的步骤比较简单，这里不赘述如何将它们转化为迭代。

另外需注意(3.3)情况，虽然其符合上述BST运算的定义，但其并未真正删掉“应该被删掉的\(x\)”，这在一定程度上会让人费解。从直觉上来说，任何节点在从创建到删除的过程中\(key\)都更应该保持不变，在具体使用BST时若不注意到这点可能会造成一些具体的问题。不过想要“真正删掉\(x\)”并不复杂，只需在原步骤上做修改，使\(y\)在被取下后不去执行替换\(key\)的步骤，而是直接用\(y\)来取代\(x\)的位置，大致步骤是先让\(y\)的3个指针和\(x\)一致，然后找到这3个指针指向的节点，把它们原本指向\(x\)的指针指向\(y\)。最后考虑到(3.3)中的步骤更方便之后讨论其他基于BST的结构，所以这里仍维持(3.3)的步骤不变。

二叉搜索树的平衡性

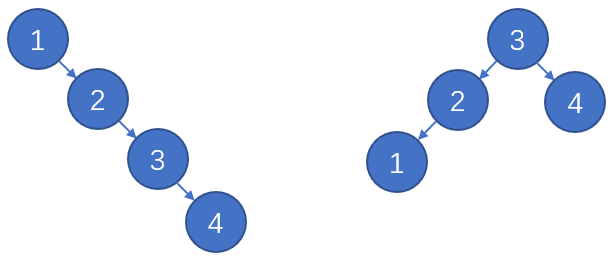
设某个二叉树的节点数和高度分别为\(n,h\)，根据之前对二叉树性质的讨论有\(\lfloor\log_2n\rfloor + 1 \leq h \leq n\)。上图的链表形态和完全二叉树形态能分别取到最大和最小高度。由于上述运算的代价为\(O(h)\)，所以自然希望每次执行运算前BST是完全二叉树。实际上完全二叉树的要求过于的“强”且不好实现，放宽要求也能达到同样的效果，下面不妨展开讨论这个问题。

假设我们构造了可数无穷个集合\(S_1,S_2,…\)，其中任意集合\(S_i\)都非空且集合元素都是“可由\(i\)个节点构成的二叉树形态”，并且对于所有这些集合，存在固定常数\(A\)使其中任意集合\(S_i\)中的任意元素的高度不大于\(A\lg{i}\)。如果一个BST每次执行上述运算前其形态都属于\(S_1\cup S_2 \cup…\)，那就能保证每次运算的代价是\(O(\lg{n})\)。显然能构造一组\(S_1,S_2,…\)描述完全二叉树。假如在构造好\(S_1,S_2,…\)后能继续在渐进代价不变的前提下修改上述运算，使运算结束时能额外保证二叉树形态属于\(S_1\cup S_2 \cup…\)，则称该BST为自平衡二叉树(self-balancing tree)。之后会讨论几种自平衡二叉树，这里不再展开，继续讨论普通BST。

下面分析BST高度的统计特征，有个经典问题是“在BST随机执行一组\(insert,remove\)后其期望高度是多少”，该问题很复杂且有段趣史。最开始人们认为只用考虑\(insert\)的影响而无需考虑\(remove\)并得到\(O(\lg{n})\)的期望高度，Knuth在其《TAOCP》的早期版本也引用过这个观点。到了20世纪80年代，有学者找到一个\(O(\sqrt{n})\)的界，并认为原因是“\(remove\)在删除有2个孩子的节点时，总固定在同一侧子树做等效删除(上文\(remove\)中的第3种情况总选择左子树)，这种模式的积累会使BST产生超出预期的偏移”。这里仍讨论下该经典问题在“不执行\(remove\)”前提下的情况，这部分内容可由如下定理给出：

b1) 在空BST对\(n\)个数执行\(insert\)，若这些数互不相等且按随机次序\(insert\)，最终BST的期望高度为\(O(\lg{n})\)；

证明：定义带下标的随机变量\(H_i\)为“在空BST对\(i\)个数执行\(insert\)，若这些数互不相等且按随机次序\(insert\)，最终BST的高度”，显然这\(i\)个数的具体值对问题无影响，保证它们不同即可，故原问题等于求\(H_n\)的期望\(E[H_n]\)。然后将原问题的\(n\)个数递增排序为\(x_1…x_n\)，显然每个数被首次执行\(insert\)(成为树根)的概率相等，假设此时刚完成首次\(insert\)且插入的是\(x_k\)，根据BST性质该BST的左子树将由\(x_1…x_{k-1}\)为\(key\)的\(k-1\)个节点构成，右子树将由\(x_{k+1}…x_{n}\)为\(key\)的\(n-k\)个节点构成，此时高度的期望是\(E[1+max(H_{k-1},H_{n-k})]\)。综上有\(E[H_n]=\frac{1}{n}\sum_{i=1}^{n}E[1+max(H_{i-1},H_{n-i})]\)。

考虑到上式不方便做数学处理，这里定义\(Y_i=2^{H_i}\)将上式转化为\(E[Y_n]=\frac{1}{n}\sum_{i=1}^{n}E[2max(Y_{i-1},Y_{n-i})]\)，根据期望的线性性有\(E[Y_n]=\frac{2}{n}\sum_{i=1}^{n}max(E[Y_{i-1}],E[Y_{n-i}])\)，去掉\(max\)可得不等式\(E[Y_n]\leq\frac{2}{n}\sum_{i=1}^{n}(E[Y_{i-1}]+E[Y_{n-i}])\)，注意到右边的每一项\(Y\)都被加了2次，所以可以把不等式整理成\(E[Y_n]\leq\frac{4}{n}\sum_{i=0}^{n-1}E[Y_i]\)。

先证明等式\(C_{n+3}^{4}=\sum_{i=0}^{n-1}C_{i+3}^{3}\)。根据组合数定义有\(C_{n+1}^{m}-C_{n}^{m-1}=C_{n}^{m}\)，故求和式末项\(C_{n+2}^{3}\)可移至左边与\(C_{n+3}^{4}\)相减得到\(C_{n+2}^{4}=\sum_{i=0}^{n-2}C_{i+3}^{3}\)，重复该过程等式两边最终为0，证明完毕。然后用归纳法证明\(E[Y_n]\leq C_{n+3}^{3}\)，\(n=0,1\)时显然，设\(n=0…k-1\)时成立，则\(\frac{4}{k}\sum_{i=0}^{k-1}E[Y_i]\leq\frac{4}{k}\sum_{i=0}^{k-1}C_{i+3}^{3}\)，结合上述不等式有\(E[Y_k]\leq\frac{4}{k}\sum_{i=0}^{k-1}C_{i+3}^{3}\)，结合上述等式有\(E[Y_k]\leq\frac{4}{k}C_{k+3}^{4}\)，利用组合数定义有\(\frac{4}{k}C_{k+3}^{4}=C_{k+3}^{3}\)，故\(E[Y_k]\leq C_{k+3}^{3}\)，即\(n=k\)成立，归纳完毕。

最后把上述\(E[Y_n]\)的界转化成\(E[H_n]\)的界，先将上述不等式写成\(E[2^{H_n}]\leq C_{n+3}^{3}=O(n^3)\)，根据期望形式的Jensen不等式，由于\(2^x\)是凸函数所以\(2^{E[H_n]}\leq E[2^{H_n}]\)，综上\(2^{E[H_n]}\leq O(n^3)\)，两边取对数可得\(E[H_n]=O(\lg{n})\)。

二叉搜索树的旋转

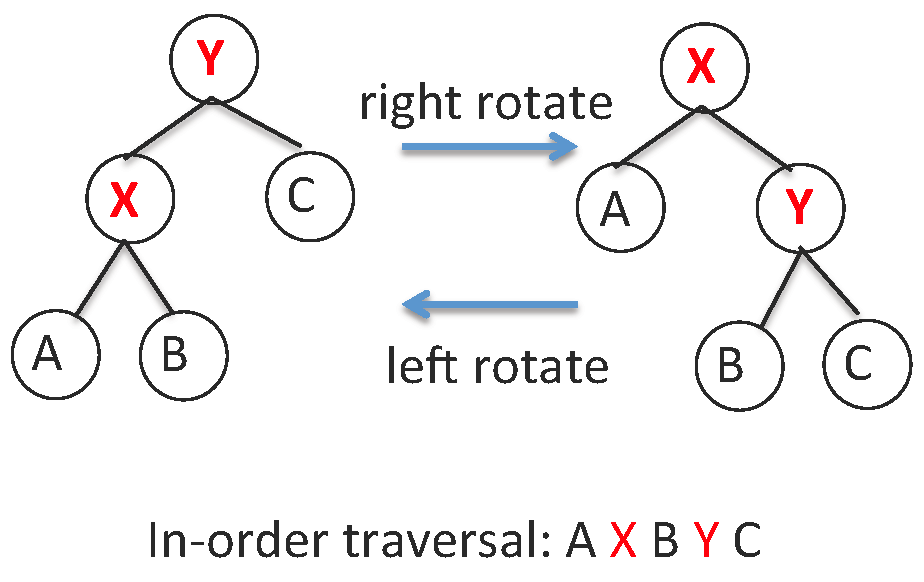
考虑到几乎所有自平衡二叉树在实现时都通过旋转运算(rotate)来实现自平衡，所以在讨论自平衡二叉树前可先讨论该运算，旋转分为左旋(left rotate)和右旋(right rotate)两种，上图给出了“右旋Y子树”和“左旋X子树”的例子，显然右(左)旋\(n\)子树的前提是\(n\)有左(右)孩子，旋转后树根会发生变化。下面给出左旋和右旋的实现，其执行前不检查左右孩子是否存在：

1) \(rightRotate(n)\)：先初始化\(m=n.left\)。然后修改孩子或数根指针，置\(n.left=m.right\)，置\(m.right=n\)，若\(n.parent\)为空则置树根为\(m\)，否则若\(n.parent.left=n\)则置\(n.parent.left=m\)，否则置\(n.parent.right=m\)。最后修改\(parent\)指针，置\(m.parent=n.parent\)，置\(n.parent=m\)，若\(n.left\)非空则置\(n.left.parent=n\)；

2) \(leftRotate(n)\)：先初始化\(m=n.right\)。然后修改孩子或数根指针，置\(n.right=m.left\)，置\(m.left=n\)，若\(n.parent\)为空则置树根为\(m\)，否则若\(n.parent.left=n\)则置\(n.parent.left=m\)，否则置\(n.parent.right=m\)。最后修改\(parent\)指针，置\(m.parent=n.parent\)，置\(n.parent=m\)，若\(n.right\)非空则置\(n.right.parent=n\)；

下面给出几个关于旋转运算的重要性质，包括旋转运算与BST的关系：

c1) 对二叉树的任意节点执行任意旋转运算(符合旋转的前提)，二叉树的中序序列不变；

c2) 利用旋转运算可将二叉树转化为任意一种由相同节点组成的其他形态；

证明：根据旋转步骤可知通过多次旋转(包括0次)能将任意节点变成树根，设二叉树中序序列为\(x_1…x_n\)，结合(c1)可知若把任意节点\(x_i\)旋转成树根，则旋转后的左子树有\(i-1\)个节点，即能通过旋转控制左子树的节点数为\(0,1…n-1\)中的任何值。接下来假定对于节点数固定为\(k\)的二叉树，无论其旋转前的形态如何，通过多次旋转(包括0次)所能得到的二叉树形态数是唯一的，并且将该形态数计为\(F(k)\)。结合之前对二叉树形态的讨论可得\(F(k)=\sum_{i=0}^{k-1} F(i)F(k-i-1)\)，其规定\(F(0)=1\)。该递推式即\(k\)个节点能构成的所有二叉树形态的数目，所以只要能验证上述假定就能完成证明，根据上面的讨论步骤可以确定，只要递推式右边的\(F\)满足假定，则左边的\(F\)就满足。所以手动验证一下前几项是否满足假定即可。

c3) 对BST任意节点执行任意旋转运算(符合旋转的前提)，BST的性质仍然保持；

c4) 利用旋转运算可将BST转化为任意一种由相同节点组成的其他形态的BST；

总结与实现

下面给出BST程序，其中的运算采用迭代实现，另外BST本身不含旋转运算，但之后关于自平衡二叉树的文章可能使用该程序，所以这里先做了实现。BST本身并不复杂，但编程细节较多，比如\(parent\)指针就容易忘记维护，另外在需要一次性修改多个指针时，如果修改次序得当，能避免使用更多的临时指针。其他之前没提到的细节可参见代码或注释。