红黑树

红黑树(Red-Black Tree)

1972年德国学者R.Bayer提出平衡二叉B树，1978年Leo J. Guibas和Robert Sedgewick将其重新表述为更容易描述和实现的红黑树。红黑树基本是目前最流行的自平衡二叉树，很多程序语言的数据类型、操作系统的算法都是基于红黑树的。下面先定义松弛红黑树(relaxed red-black tree)，然后在松弛红黑树的基础上定义红黑树：

1) 松弛红黑树节点：额外包含一个布尔值的BST节点。为方便称其表示红或黑，对应的节点为红节点或黑节点；

2) 松弛红黑树：由松弛红黑树节点构成的BST，且满足如下性质：

2.1) 红节点如果有孩子，则孩子只能是黑节点；

2.2) 对于任意节点\(x\)，从\(x\)到\(x\)子树的所有叶节点的路径中，黑节点数必须相同；

3) 红黑树：必须是松弛红黑树，且满足如下性质：

3.1) 要么是空树，要么树根是黑节点；

根据(2.2)任何松弛红黑树中的任意节点\(x\)到\(x\)子树任意叶节点的路径中的黑节点数目固定，该数目被称为\(x\)子树的黑高(black-height)，规定空树的黑高为0。定义(2.2)通常也被成为黑高平衡性。设松弛红黑树节点的左(右)子树高度为\(h\geq 0\)，则(2.2)能在(2.1)的基础上保证右(左)子树高度不超过\(2h+1\)。所以上述松弛红黑树性质是为保证左右子树的高度比最大在2附近，而AVL树则是保证左右子树的高度差最大不超过2。下面继续给出松弛红黑树的性质，其都很容易验证：

a1) 松弛红黑树的左右子树都是松弛红黑树，且两者黑高相等；

a2) 对于任意红树根的松弛红黑树，置黑其树根即成为红黑树；

上图是红黑树形态的特例，其高度恰好是黑高的2倍，从直观上看红黑树左右子树的规模差距可能比AVL树更大。一般的自平衡二叉树仅仅是为了让BST运算的代价更低，故本文对其运算的定义和前文对BST运算的定义一致，但要额外保证每次运算前后二叉树是红黑树，且运算代价和BST运算一样以树高为上界，否则构造红黑树就失去意义。另外可发现BST的\(find\)不会改变树结构，符合红黑树运算的要求，故之后只需讨论另外2种运算的实现。下述性质将保证红黑树是自平衡二叉树：

a3) 包含\(n\geq 0\)个节点的红黑树的高度以\(2\log_2{(n+1)}\)为上界，并且这个界足够准确；

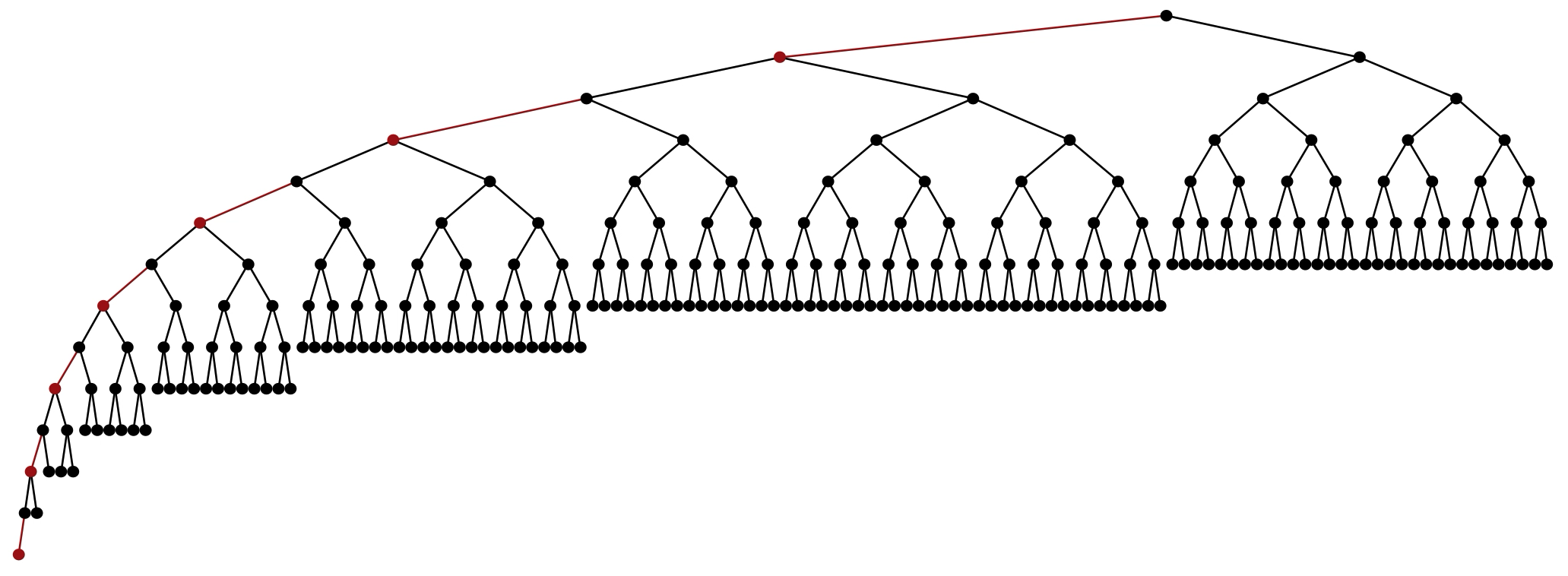
证明：设\(N_{bh}\)是黑高\(bh\geq 0\)的松弛红黑树所需的最小节点数。则\(N_0=0\)。由\(N_{bh}\)的定义容易用反证法验证\(N\)严格单调递增。设松弛红黑树\(T\)的黑高为\(bh>0\)，节点数为\(N_{bh}\)。假设\(T\)有红树根，则\(T\)左子树右子树的黑高都为\(bh\)且节点数都必须为\(N_{bh}\)，与\(N\)严格单调递增矛盾，所以\(T\)一定有黑树根，故\(T\)左子树右子树的黑高都为\(bh-1\)且节点数必须都为\(N_{bh-1}\)，于是可得递推式\(N_{bh}=2N_{bh-1}+1\)，设\(S_{bh}=N_{bh}+1\)以去掉常数，则\(S_{bh}=2S_{bh-1}\)，求等比数列得\(S_{bh}=2^{bh}\)，故\(N_{bh}=2^{bh}-1\)。所以黑高为\(bh\)的含最少节点的松弛红黑树是仅含黑节点且高度为\(bh\)的完美二叉树。继续取对数可得到\(bh=\log_2{(N_{bh}+1)}\)，然后设包含\(n\geq 0\)个节点的松弛红黑树的最大黑高和最大高度分别为\(BH(n),H(n)\)。根据\(N,BH\)的定义有\(N_{BH(n)}\leq n\)，带入上述等式有\(BH(n)=\log_2{(N_{BH(n)}+1)}\leq \log_2{(n+1)}\)。根据松弛红黑树的定义有\(H(n)\leq 2BH(n)=2\log_2{(n+1)}\)，最后根据性质(a2)该式对红黑树成立。为确定该界足够准确，考虑构造高度为黑高2倍的红黑树，上图实际上就提供了构造方法，即对于任意黑高\(k\geq 1\)，先构造树根为黑且红黑相间的由\(2k\)个节点组成的“左链表树”，并从左到右依次在每个节点的空右孩子接入高度为\(0,0,1,1,…,k-1,k-1\)的仅含黑节点的完美二叉树，显然其节点数\(n=2\Sigma_{i=0}^{k-1} (2^i-1) + 2k=2^{k+1}-2\)，取对数可得高度\(2k\)等于\(2\log_2{(n+2)} – 2\)，所以该方式构造的树在\(n\)无穷时与\(2\log_2{(n+1)}\)的比值为1，故该界准确。

上述性质说明红黑树比AVL树“更高”，因为前者的\(\log_2{(x)}\)函数的系数约为1.441，后者的则为2，红黑树的优势更多在于运算。根据(a1)松弛红黑树和AVL树有相似的“递归结构”，有该性质时通常更易设计算法，但红黑树不满足(a1)。根据(a2)松弛红黑树和红黑树形态相同，红黑树不比松弛红黑树有更低的高度。总之(3.1)显得多余，不过(3.1)一定程度能方便实现运算。

红黑树的插入运算

先直接给出红黑树上的\(insert(k)\)运算的步骤如下：

1) 在红黑树执行BST的\(insert(k)\)运算(按之前讨论BST的文章中的步骤)，然后将新增的节点计为\(x\)；

2) 初始化\(x\)为红色。开始迭代过程，每轮迭代的步骤如下：

2.1) \(x\)无父亲或有黑父亲：若\(x\)无父亲则置黑\(x\)。退出迭代；

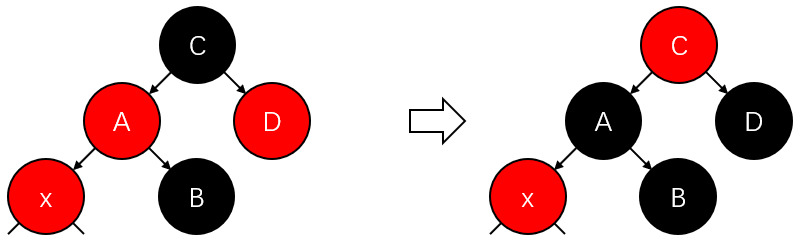
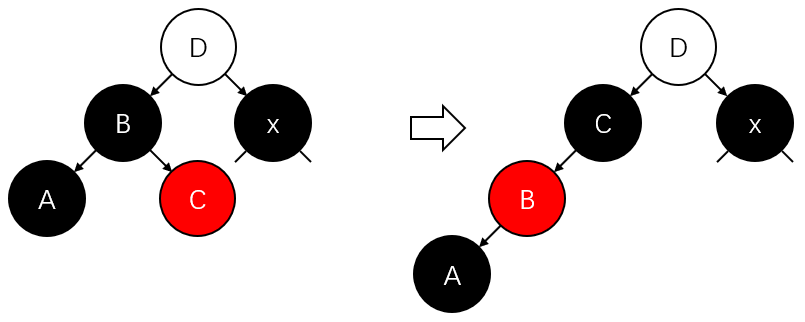
2.2) \(x\)有红父亲且有红叔叔：置\(x\)的父亲、叔叔、祖父为黑、黑、红。置\(x\)为其祖父。继续迭代(见上图第1张)；

2.3) \(x\)有红父亲且无叔叔或有黑叔叔：需分情况讨论：

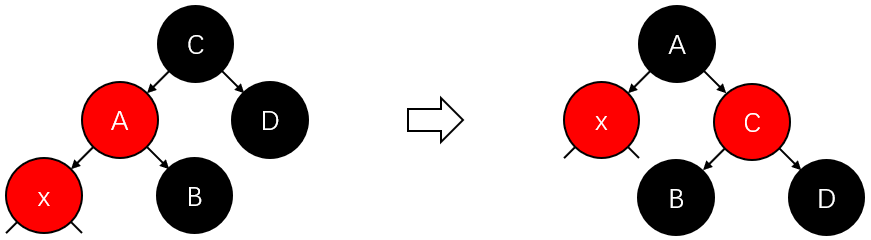
2.3.1) \(x\)与其父亲都是左节点：置\(x\)的父亲、祖父为黑、红。右旋转\(x\)的祖父。退出迭代(见上图第2张)；

2.3.2) \(x\)与其父亲都是右节点：置\(x\)的父亲、祖父为黑、红。左旋转\(x\)的祖父。退出迭代(参考上图第2张)；

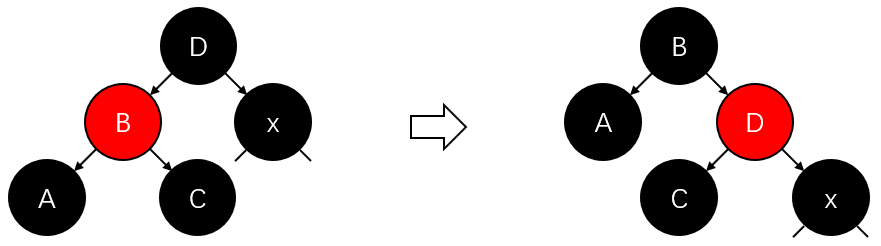
2.3.3) \(x\)与其父亲分别是右左节点：左旋转\(x\)的父亲(见上图第3张)。置\(x\)为旋转前\(x\)的父亲。照搬(2.3.1)；

2.3.4) \(x\)与其父亲分别是左右节点：右旋转\(x\)的父亲(参考上图第3张)。置\(x\)为旋转前\(x\)的父亲。照搬(2.3.2)；

接下来验证上述步骤的正确性。首先在BST插入完成时初始化新节点为红色能更方便实现运算。然后考虑验证命题“每轮迭代开始时的\(x\)是红树根的松弛红黑树且其黑高与BST插入前相等”，并在此基础上明确每轮迭代的作用。

第1轮迭代开始时满足上述命题，因为BST插入前\(x\)的位置是空节点。假如该轮迭代进入(2.1)，若\(x\)无父亲，则\(x\)子树是整个树，显然该轮迭代结束时整个树是红黑树，若\(x\)有黑父亲，则该轮迭代结束时的\(x\)的父亲是黑树根的松弛红黑树，其黑高相比BST插入前不变，于是可确定此时的\(x\)的父亲的所有祖先(可能无祖先)都不违反松弛红黑树定义，因为它们的黑高都与BST插入前一致，且都不出现“红节点相邻”的情形，进而可确定此时整个树是红黑树。假如该轮迭代开始时\(x\)有红父亲，则\(x\)必然有黑祖父，否则BST插入前整个树就已违反红黑树定义，故该轮迭代只能进入(2.2)或(2.3)。假如该轮迭代进入(2.2)，该轮迭代结束时的\(x\)是红树根的松弛红黑树，其黑高与BST插入前相等，于是下轮迭代存在且在开始时也满足上述命题。假如该轮迭代进入(2.3)，该轮迭代结束时的\(x\)的父亲是黑树根的松弛红黑树，注意到此时的\(x\)的父亲和该轮迭代开始时的\(x\)的祖父都表示同个子树，并且此时该子树的黑高与BST插入前相等，于是可确定此时的\(x\)的父亲的所有祖先(可能无祖先)都不违反松弛红黑树的定义，因为它们的黑高都与BST插入前一致，且都不出现“红节点相邻”的情形，进而可确定此时整个树是红黑树。

第2轮迭代开始时(假如该轮迭代存在)也满足上述命题，因为上轮迭代只能是(2.2)情况。该轮迭代的情形也符合上述论述。第3轮……综上整个运算结束时，整个树必为红黑树。该运算的代价显然是二叉树高度\(O(h)\)，且至多执行2次单旋转。

红黑树的删除运算

* 白节点可以是任何颜色

先直接给出红黑树上的\(remove(k)\)运算的步骤如下：

1) 在红黑树执行BST的\(remove(k)\)运算(按之前讨论BST的文章中的步骤)，然后将失去的节点计为\(x\)(为空则删除失败)；

2) 若\(x\)为红节点什么也不做。否则若BST删除前\(x\)有1个孩子则置黑该孩子。否则开始迭代过程，每轮迭代的步骤如下：

2.1) \(x\)无父亲：退出迭代；

2.2) \(x\)有父亲且有黑兄弟：需分情况讨论：

2.2.1) \(x\)的兄弟无红孩子：置红\(x\)的兄弟。若\(x\)有黑父亲则置\(x\)为\(x\)的父亲并继续迭代，否则置黑\(x\)的父亲并退出迭代；

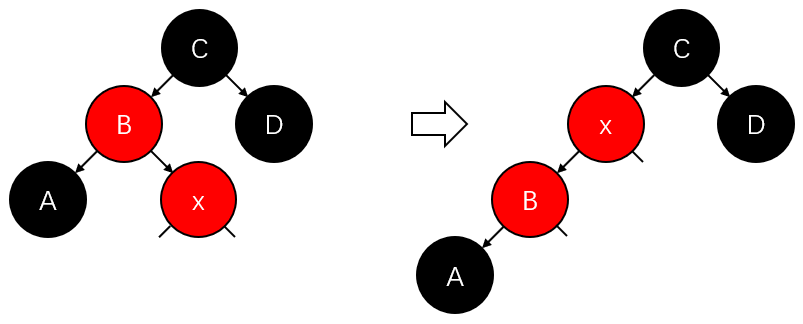
2.2.2) \(x\)的兄弟是左节点且有红左孩：置黑\(x\)的兄弟的左孩。交换\(x\)的父兄的颜色。右旋转\(x\)的父亲。退出迭代(见上图第1张)；

2.2.3) \(x\)的兄弟是右节点且有红右孩：置黑\(x\)的兄弟的右孩。交换\(x\)的父兄的颜色。左旋转\(x\)的父亲。退出迭代(参考上图第1张)；

2.2.4) \(x\)的兄弟是左节点且有红右孩：交换\(x\)的兄弟与其右孩的颜色。左旋转\(x\)的兄弟(见上图第2张)。照搬(2.2.2)；

2.2.5) \(x\)的兄弟是右节点且有红左孩：交换\(x\)的兄弟与其左孩的颜色。右旋转\(x\)的兄弟(参考上图第2张)。照搬(2.2.3)；

2.3) \(x\)有父亲且有红兄弟：需分情况讨论：

2.3.1) \(x\)的兄弟是左节点：交换\(x\)的兄弟与父亲的颜色。右旋转\(x\)的父亲(见上图第3张)。照搬(2.2)；

2.3.2) \(x\)的兄弟是右节点：交换\(x\)的兄弟与父亲的颜色。左旋转\(x\)的父亲(参考上图第3张)。照搬(2.2)；

接下来验证上述步骤的正确性。先明确上述步骤(2)的作用，首先根据BST删除的步骤，BST删除前\(x\)至多有1个孩子。若\(x\)为红节点，BST删除后显然不违反红黑树定义，否则若BST删除前\(x\)有1个孩子，说明\(x\)是黑节点且该孩子必为红叶节点，否则BST删除前就已违反红黑树定义，BST删除后该孩子取代\(x\)的位置，此时置黑该孩子可保证不违反红黑树定义。否则说明\(x\)是黑叶节点，BST删除后空节点取代\(x\)的位置，此时若整个树非空，则必然违反红黑树定义，需要后续的迭代过程。

注意对于首轮迭代，该轮迭代开始时上文中的“\(x\)的兄弟”等概念有歧义，因为此时的\(x\)已经被空节点取代，不妨规定此时这些概念指“取代\(x\)的空节点的兄弟”等。然后考虑验证命题“首轮迭代开始时‘取代\(x\)的空节点’的黑高等于BST删除前的\(x\)的黑高-1，之后的每轮迭代开始时的\(x\)是黑树根的松弛红黑树且其黑高相比BST删除前-1”，并在此基础上明确每轮迭代的作用。

第1轮迭代开始时显然满足上述命题。假如该轮迭代进入(2.1)，则该轮迭代结束时显然整个树是空的红黑树。假如该轮迭代开始时“取代\(x\)的空节点”有父亲，则“取代\(x\)的空节点”的兄弟必然存在，否则BST删除前整个树就已违反红黑树定义，所以该轮迭代只能进入(2.2)或(2.3)。假如该轮迭代进入(2.2.1)，如果该轮迭代最终是继续迭代，则该轮迭代结束时的\(x\)是黑树根的松弛红黑树，其黑高相比BST删除前-1，于是下轮迭代存在且开始时也满足上述命题，如果该轮迭代最终是退出迭代，则该轮迭代结束时的“取代\(x\)的空节点”的父亲是黑树根的松弛红黑树，其黑高相比BST删除前不变，于是可确定此时的“取代\(x\)的空节点”的父亲的所有祖先(可能无祖先)都不违反松弛红黑树的定义，因为它们的黑高都与BST插入前一致，且都不出现“红节点相邻”的情形，进而可确定此时整个树是红黑树。假如该轮迭代进入(2.2.2)-(2.2.5)，则该轮迭代结束时的“取代\(x\)的空节点”的祖父是松弛红黑树，注意到此时的“取代\(x\)的空节点”的祖父和该轮迭代开始时的“取代\(x\)的空节点”的父亲都表示同个子树，并且此时该子树的黑高与BST删除前相等，树根的颜色也与BST删除前一致，于是可确定此时的“取代\(x\)的空节点”的父亲的所有祖先(可能无祖先)都不违反松弛红黑树的定义，因为它们的黑高都与BST插入前一致，且都不出现“红节点相邻”的情形，进而可确定此时整个树是红黑树。假如该轮迭代进入(2.3)，则该轮迭代开始时的“取代\(x\)的空节点”的父亲必然是黑节点，“取代\(x\)的空节点”的兄弟必然有2个黑孩子，否则BST删除前整个树就已违反红黑树定义，该轮迭代结束时的“取代\(x\)的空节点”的曾祖父是黑树根的松弛红黑树，注意到此时的“取代\(x\)的空节点”的曾祖父和该轮迭代开始时的“取代\(x\)的空节点”的父亲都表示同个子树，并且此时该子树的黑高与BST删除前相等，于是可确定此时的“取代\(x\)的空节点”的曾祖父的所有祖先(可能无祖先)都不违反松弛红黑树的定义，因为它们的黑高都与BST插入前一致，且都不出现“红节点相邻”的情形，进而可确定此时整个树是红黑树。

第2轮迭代开始时(假如该轮迭代存在)也满足上述命题，因为上轮迭代只能是(2.2.1)中的继续迭代情况。该轮迭代的情形也基本符合上述论述(基本上把上述论述文字中的“取代\(x\)的空节点”改成\(x\)即可)。第3轮……综上整个运算结束时，整个树必为红黑树。该运算的代价显然是二叉树高度\(O(h)\)，且至多执行3次单旋转。

总结与实现

这里提出几个关于程序实现红黑树的要点和个人的小建议：

1) 对于\(remove\)运算，BST删除刚完成时的\(x\)已不在树上，但根据BST删除的具体步骤，此时\(x\)中的指针仍和BST删除前一致。所以\(remove\)运算的步骤(2)中的“判断BST删除前的\(x\)是否有1个孩子”的逻辑可直接利用此时的\(x\)完成。另外对于\(remove\)运算中的首轮迭代，在该轮迭代开始需要获取“取代\(x\)的空节点”的父亲、兄弟等节点，其也可借助此时的\(x\)中的指针来完成，其中“取代\(x\)的空节点的兄弟”刚好是“取代\(x\)的空节点的父亲”的唯一非空孩子；

2) 对于\(insert,remove\)运算，最好全程维护表示此时的\(x\)的父亲、叔叔、兄弟等的变量，否则程序会非常繁琐；

3) 对于\(insert,remove\)运算，最好不要把“照搬其他子步骤”在程序中实现为“在下轮迭代执行其他子步骤”，这会使逻辑稍微发生一点点的改变，上文的证明过程也未严格涵盖这种实现。这里以\(remove\)的步骤(2.3)为例来说明我个人是如何实现“照搬(2.2)”的，首先把(2.3)的判断条件和步骤放入一个「IF块」，然后直接把(2.2)放在该「IF块」后面(见下述代码)；

最后给出面向对象的程序实现，之前讨论BST的文章中的BST类被作为基类，其他未提到的细节见程序与注释。