多模匹配问题与AC自动机

多模匹配与AC自动机

多模匹配指“给定单个目标串与多个模式串，确定所有模式串在目标串中的所有出现位置”，相比单模匹配的“单个模式串，首次出现”，多模匹配明显更抽象和复杂（我的看法是AC自动机比KMP难一些）。这里把目标串和模式串分别计为\(t\)和\(p_1,p_2…\)，还是老样子先简单的找一个多模匹配的朴素算法如下。

1）从\(t\)的第1位字符开始，与模式串\(p_1\)逐位对齐比较，匹配成功则记录\(p_1\)在第1位出现1次；

2）从\(t\)的第1位字符开始，与模式串\(p_2\)逐位对齐比较，匹配成功则记录\(p_2\)在第1位出现1次；

…

n）从\(t\)的第2位字符开始，与模式串\(p_1\)逐位对齐比较，匹配成功则记录\(p_1\)在第2位出现1次；

…

这个流程是很直观的，这里除了顺着找还可以倒过来找，比如对于\(t\)上的每个字符，从每个字符“向前看”来从尾到头的逐位去匹配模式串也可以，无论如何，这种朴素算法的代价是\(O(|t|\cdot\Sigma|p_i|)\)。这里之所以要提到一句“向前看”这种倒过来的方法，是因为其更“接近”AC自动机的思路。

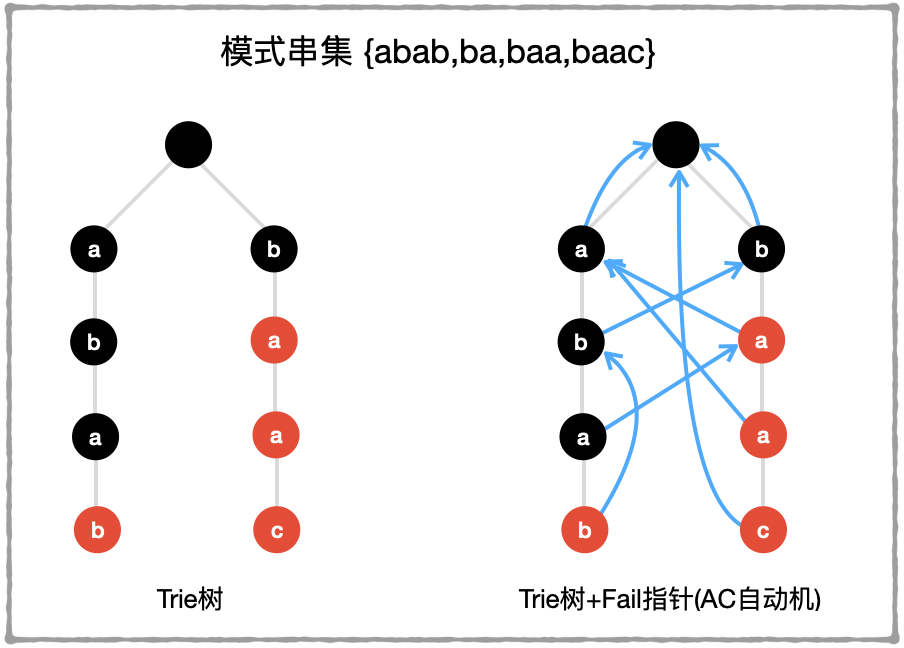
AC(Aho-Corasick)自动机诞生于1975年的贝尔实验室(Aho是龙书《编译原理》的作者)，其诞生稍早于单模匹配的KMP算法。其之所以叫“自动机”是因为可构造一台有穷自动机(DFA)诠释该算法。该算法还有个名字Trie图，是这个算法的另一等价诠释，本文从Trie图的视角讨论这个算法。

简而言之，AC自动机就是在Trie树上为每个节点增加Fail指针(边)，借助Fail边提供的信息来辅助匹配。可以认为AC自动机是对上述“向前看”朴素算法的优化。因为构造好AC自动机后，每次读完\(t\)上的一个字符，然后需要“向前看”匹配不同模式串时，AC自动机可“直接提供”这些信息。这里先给出AC自动机“构建+匹配”的总代价是\(O(|t|+\Sigma|p_i|)\)，等价于遍历主串和所有模式串的代价。

AC自动机 — 匹配流程

为方便讨论先明确几个与AC自动机算法有关概念或术语：

真前缀：本文中字符串的真前缀指字符串除本身外的前缀，如aab的所有真前缀是a,aa；

前缀：本文中字符串的前缀=字符串的真前缀+字符串本身；

Trie树：略（对Trie树的定义和实现见之前的文章）；

Trie节点：基于之前文章的讨论，这里进一步明确Trie节点的意义。设某Trie树存储了若干字符串，每个字符串又有若干个前缀，设这些字符串的所有前缀构成集合\(S\)(相同字符串已去重)，则每条“树根-Trie节点”路径与\(S\)的元素可形成一一映射，每个Trie节点与\(S\)的元素可形成一一映射，这就是为什么Trie树叫前缀树。为方便用\(PRE[N]=x\)表示Trie节点\(N\)映射到\(S\)中的元素\(x\)。

Fail指针：设\(X,Y\)(\(X\)非根)是不同的Trie节点。若对于所有节点，\(PRE[Y]\)是\(PRE[X]\)的最长真后缀，那么\(X\)存在Fail指针指向\(Y\)，\(Y\)为根节点时表示\(X\)的“最长真后缀”为空；

AC自动机：所有模式串构成Trie树+Fail指针就是一个构造好的AC自动机；

接下来是额外给出Fail指针的一些比较容易得出的性质：

1) 每个非根节点有且只有1个Fail指针；

2) 第\(n\)层节点的Fail指针只能指向小于等于\(n-1\)层的节点；

3) 每个非根节点都有且仅有1条Fail链表，链表节点靠Fail指针连接，链表尾一定是树根。

然后可以给出用“已构造好的AC自动机”对目标串进行多模匹配的流程：

1）初始化：指针\(curr\)指向Trie树根，目标串\(t\)的下标\(i=-1\)；

2）若\(curr\)此时指向根节点则该步骤不执行任何操作。若\(curr\)此时不指向根节点，则遍历其Fail链表，判断每个链表节点代表的前缀串是否为模式串，并记录出现过的模式串在目标串中的位置；

3）令\(i=i+1\)，若\(t[i]\)未越界则令\(w=t[i]\)，否则算法完成并结束；

4.1）若\(curr\)有字符\(t[i]\)子节点：将\(curr\)指向该节点，回步骤(2)；

4.2）若\(curr\)无字符\(t[i]\)子节点：若\(curr\)为根(无Fail指针)，回步骤(3)。若\(curr\)非根，则遍历其Fail链表，每到达一个节点就检查其有无孩子Trie节点匹配\(t[i]\)，如果有则将\(curr\)指向它，回步骤(2)。如果一直遍历到根节点并且根节点也没有孩子表示\(t[i]\)字符，将\(curr\)指向根，回步骤(3)。

AC自动机 — 匹配流程 — 正确性分析

这里通过引理和循环不变式证明上述流程的正确性，这2个引理较容易得到就不证明了：

引理1：设从目标串的\(j\)位置向前查找，可以得到子串\(…t[j-2]t[j-1]t[j]\)，设\(s\)为向前查找能够找到的\(PRE\)中的最长的串。那么从\(j\)向前查找所找到的所有模式串都必然是\(s\)的后缀，反之从\(j\)向前查找如果能找到至少一个模式串，那么一定能找到至少一个PRE。

引理2：对于任意Fail链表，将其节点从头到位依次计为\(N_0,N_1,…\)。那么\(PRE[N_0]\)在所有\(PRE\)中的所有真后缀是\(PRE[N_1],PRE[N_2],…\)。

分析每次“进入步骤(3)-即将下次进入步骤(3)”的循环节，算法首先会读目标串的下个字符\(t[j]\)，然后\(curr\)经过0~n次Fail边跳转，到达根节点，或到达\(t[j]\)节点并执行步骤(2)。下一轮步骤(3)即将开始….

每个循环节从开始到结束发生了这些事情，目标串的\(t[j]\)被读取，指针\(curr\)停在某个Trie节点\(N\)上，若能够证明\(PRE[N]\)的实际意义就是引理1中\(s\)的意义，那么只要结合引理2就能确定通过步骤(2)就能够跟朴素算法一样，找到从\(t[j]\)向前看能找到的全部模式串。这里进行证明：

1) 设第\(1\)次进入循环节，马上读取\(t[0]\)，若从\(curr\)未找到\(t[0]\)孩子，则\(curr\)仍指向根节点并跳过步骤(2)，本循环节结束，\(curr\)停留在根结点，\(t[0]\)非任何\(PRE\)，符合题意。若从\(curr\)找到\(t[0]\)孩子，则\(curr\)指向这个孩子，进入步骤(2)，此时\(t[0]\)是\(PRE\)且显然是从\(t[0]\)向前看能找到的最长\(PRE\)。

……

2) 假设第\(k\)次进入循环节，马上读取\(t[k-1]\)，最后\(curr\)停留在节点\(N\)，而\(PRE[N]\)确实是\(t[k-1]\)向前看所能找到的最长\(PRE\)。

3) 设第\(k+1\)次进入循环节，马上读取\(t[k]\)，此时\(curr\)指向\(N\)。需在\(N\)下找\(t[k]\)孩子节点。

3.1) 若找到了就将\(curr\)指向该节点\(N’\)，此时\(PRE[N’].len=PRE[N].len+1\)，否则与上次循环节结果矛盾，所以“\(PRE[N’]=PRE[N] + t[k]\)”。\(PRE[N’]\)是\(t[k]\)向前看能找到的最长\(PRE\)。

3.2) 若未找到但在遍历\(N\)的Fail链表时(包括树根)找到了\(t[k]\)孩子节点(计为\(N’\))，然后将\(curr\)指向\(N’\)。此时可以知道从\(t[k]\)向前看所能找到的最长\(PRE\)是\(t[k]\)单字符或者是\(PRE[N]\)的某个后缀再加上\(t[k]\)字符，否则将会与上次循环节的结果矛盾。根据引理2，\(PRE[N]\)在PRE中的所有后缀都被\(N\)的Fail链表所表示，那么沿着Fail链表可以从长到短的遍历\(PRE[N]\)在PRE中的所有后缀，每次到达一个链表节点如果能找到表示\(t[k]\)的子节点\(N’\)，那么\(PRE[N’]=PRE[N]+t[k]\)是\(t[k]\)向前看可找到的最长\(PRE\)。

3.3) 若未找到且在遍历\(N\)的Fail链表时(包括树根)也未找到表示\(t[k]\)的孩子节点，则\(PRE[N]\)在PRE中的所有后缀加上\(t[k]\)以及\(t[k]\)本身都不能作为一个PRE，即从\(t[k]\)向前看找不到任何匹配的模式串。

综上每个循环节中的步骤(3)(4)结束后，\(t\)被读取了一个\(t[j]\)的字符，\(curr\)停留在某个节点\(N\)上，其对应\(PRE[N]\)就是\(t\)从\(j\)向前找能找到的最长PRE。再看步骤(2)如何利用这个结果统计出“\(t\)从\(j\)的位置向前看所能找到的全部模式串”，根据引理1可匹配的所有模式串一定是\(PRE[N]\)的后缀，那么\(N\)的Fail链表一定包含所有的可匹配的模式串，步骤(2)确实能够统计出所有模式串。

AC自动机 — 匹配流程 — 时间复杂度分析

这里容易发现对于每个循环节，如果先忽略掉其中的步骤(2)，除了无法确定在步骤(4)跳了几次Fail外，其他所有操作的代价共为\(O(1)\)。当然这里需要明确一点，就是对于我们所实现的Trie树数据结构，其从任何节点的子节点中找到表示某个字符的孩子仅需要\(O(1)\)的代价。

然后通过摊还分析确定对于所有循环节中的步骤(4)，一共发生了多少次Fail跳跃。容易发现每个循环节至多跳1次Trie边，即\(curr\)至多向下走1层，而每次跳Fail边至少向上走1层。所以总的跳Trie边的次数一定要大于总的跳Fail边的次数，所以跳Trie边的总次数和跳Fail边的总次数有一个共同上界\(O(|t|)\)。所以忽略步骤(2)的话，AC自动机的匹配流程的代价是\(O(|t|)\)。

最后看步骤(2)，步骤(2)也需要遍历Fail链表，感觉时间复杂度可能会超\(O(|t|)\)，事实上确实超了。比如设目标串是100万个a，有1000个模式串分别是a,aa,…一千个a，那么在\(curr\)读到目标串第1000个字符后，每读1个字符就需要遍历模式串的总长度，那么匹配流程的总代价就是\(O(|t|\cdot\Sigma|p_i|)\)。

这里用“作弊方法”回避该问题。步骤(2)其实是“独立的”，它只是单纯看看在目标串\(i\)下标从后向前都出现了哪些模式串。所以不妨改变步骤(2)，让它只记录该Fail链表的表头节点，而不遍历。并且在建Trie树的时候让每个词尾节点\(N\)附带一个变量\(N.word\)完整记录这个单词本身。这样的话步骤(2)就变成了“若\(curr\)此时指向根节点则该步骤不执行任何操作。若\(curr\)此时不指向根节点，则记录当前\((curr,i)\)到\(X\)”。这样新步骤(2)的代价就是\(O(1)\)，总匹配流程的代价是\(O(|t|)\)。

在新的步骤(2)下，算法结束后会得到集合\(X\)，其中存放了很多\((Trie节点,目标串下标)\)，姑且把集合\(X\)作为多模匹配问题的解。因为如果遍历其中任何一个节点的Fail就能得到一组\(word\)，这些\(word\)就是以目标串下标\(i\)为结尾的所有模式串。当然如果遍历的话时间复杂度就超了。。。

AC自动机 — 构建流程

前面讨论了匹配流程，这里讨论如何构造AC自动机，即求Fail指针。这里先找递推关系：

设\(u\)为非根节点且已求出\(u.fail\)，若\(u,u.fail\)都有孩子表示字符\(w\)(分别计为\(u[w],u.fail[w]\))，那么必须有\(u[w].fail\)指向\(u.fail[w]\)，否则会导致求得的\(u.fail\)不正确。同理推广可得：“设有Trie树节点\(u\)，\(u\)存在表示字符\(w\)的孩子(计为\(u[w]\))，并且已求得正确的\(u\)上的fail链表。那么设节点\(v\)是链表上距\(u\)最近且包含表示字母\(w\)的孩子的节点。指针\(u[w].fail\)应当指向\(v[w]\)。

这个递推关系表明求出第\(k\)层及其以上全部节点的Fail指针后，能直接利用这个关系求出第\(k+1\)层全部节点的Fail指针。其具体的算法流程如下：

1) 在构造好的Trie树第1层节点添加指向树根的Fail指针，把第1层节点全部入队\(Q\)；

2) 出队一个顶点\(N\)，利用上述递推关系求出\(N\)全部孩子的Fail指针(具体操作略)；

3) 把\(N\)的全部孩子入队，回到步骤(2)；

AC自动机 — 构建流程 — 时间复杂度分析

跟匹配流程的时间复杂度分析一样，在Trie树按层次遍历构造Fail指针时，每次到达1个节点后，不知道跳了几次Fail。同样的还是用摊还分析思路来确定其时间复杂度。先是定义记号\(N[w]\)为Trie节点\(N\)表示字符\(w\)的子节点，\(h(N)\)是节点\(N\)从根向下的深度。然后利用上述流程来找出数值的递推关系：

1) 从Trie树上找任意的一个“树根-非根节点”链表，从上到下把这个链表节点计为\(N_1,N_2…\)。根据上述构建流程，会按层次从上到下的求出\(N_1,N_2,…\)的Fail指针(不妨直接设\(N_0\)为根节点)。并且设计算\(N_i\)的Fail指针时，其父节点\(N_{i-1}\)的Fail链表跳了\(k_i\)次。

2) 跳跃次数满足\(k_i \leq h(N_{i}) – h(N_{i}.fail) \)，取不等号是因为跳1次Fail可能不止上移1层；

3) 高度满足\(h(N_{i}.fail) \geq h(N_{i-1})\)，取不等号也是因为跳1次Fail可能不止上移1层；

4) 联立两式有\(k_i \leq h(N_{i}) – h(N_{i-1}) \)，求和有\(\sum\nolimits_{i=1..n}k_i \leq h(N_{n}) = n\)

上述求和式表明对于Trie树上任意的“树根-非根节点”链表，构建流程在按层次遍历的序求出其全部的Fail指针时，途中发生的Fail跳跃次数至多为链表节点的数目，所以构建流程在求出n个节点的Fail指针时，至多发生n次跳Fail。也就是上述步骤(2)求每个孩子的Fail指针的代价是\(O(1)\)，而由于每个Trie节点至多发生一次“出队、入队、求Fail指针”，所以构建全部Fail指针的代价有一个上界等于Trie节点的总数，而Trie节点总数又有上界为全体模式串的字符数，所以构建AC自动机的代价有上界\(O(\Sigma |p_i|)\)。

从直观看就是在求某个节点的Fail指针时，如果其父节点多次跳Fail，那么求得该节点的Fail指针一定向上跨越多层，那么在求这个节点子节点的Fail指针的遍历父节点的Fail链表环节中，第1次到达链表节点就被其父节点的Fail指针拉上去好多层…然后一层层向下产生影响，最后整体上限制了总的跳Fail次数。

AC自动机 — 具体实现

到这里已经很明确AC自动机的正确性，把两个步骤的时间复杂度加起来确实就等于\(O(|t|+\Sigma|p_i|)\)，如果在匹配流程直接用Fail作为匹配结果，那么从摊还分析的角度确实也不需要回溯。

实现AC自动机时可考虑下软件设计问题，比如要让其具有可复用性，即建1次AC动机后能多次复用匹配不同目标串。且根据之前对匹配流程的时间复杂度分析，需要把AC自动机的某些Fail链表作为匹配结果。这里通过定义MatchResult对象包装这个链表，在\(match\)完成后返回这个MatchResult对象，其包含了关于多模匹配结果的全部信息。可以确定求得MatchResult的最坏代价确实是\(O(|t|+\Sigma|p_i|)\)。但如果把这个结果打印或整理成数组等形式的话，就无法保证其最坏代价是\(O(|t|+\Sigma|p_i|)\)。