用栈实现二叉树的迭代遍历

用栈记录节点的祖先

在之前讨论节点前驱后继的文章中，通过节点上额外存储的\(parent\)指针实现了前中后序遍历的迭代算法，文章中为体现出通过“连续寻找后继”实现遍历，用多个函数组成了这3种算法，这些算法不能直接用于无\(parent\)指针的普通二叉树，本文讨论如何将这几种算法改造成适用于普通二叉树的，由于正序遍历和逆序遍历存在对称性，故不再讨论逆序遍历。先将上述算法通用的\(traverse\)函数改造为如下步骤，其仅多了创建空栈\(s\)并将其传入\(getFirst,getSuccessor\)的步骤：

1) \(traverse(root)\)：若树根\(root\)为空则直接返回，否则初始化空栈\(s\)，执行\(head=getFirst(root, s)\)，然后“访问”\(head\)，然后开始迭代，每轮迭代执行\(head=getSuccessor(head, s)\)，执行完后若\(head\)非空则“访问”\(head\)，否则返回；

上述步骤说明改造后的另外2个函数的形式是\(getFirst(n,s), getSuccessor(n,s)\)，其中\(n\)是原来的传入节点，\(s\)是\(traverse\)中创建的栈。规定这2个改造后的函数必须满足如下的性质，之后再根据3种遍历算法来具体实现它们：

a1) 改造后的\(getFirst(n,s), getSuccessor(n,s)\)若在调用开始时\(s\)满足从栈顶开始是\(n\)由近到远所有的祖先，则该次调用的返回节点(计为\(n’\))必须与改造前的函数相同，且该次调用返回时\(s\)从栈顶开始是\(n’\)由近到远所有的祖先(\(n’\)为空则\(s\)为空)；

改造后的\(traverse(root)\)在创建完空栈\(s\)后首先执行\(head=getFirst(root,s)\)，此时满足\(s\)从栈顶开始是\(root\)由近到远所有的祖先(空栈)。由于\(getFirst(n,s), getSuccessor(n,s)\)满足(a1)性质，故接下来执行\(head= getSuccessor(root,head)\)时也满足\(s\)从栈顶开始是\(head\)(括号内的)由近到远所有的祖先，这一点对于之后循环执行的\(head= getSuccessor(root,head)\)始终保持成立。所以在性质(a1)成立的基础上，改造后的\(traverse(root)\)满足的性质如下：

a2) 若改造后的\(getFirst(n,s), getSuccessor(n,s)\)满足性质(a1)，改造后的\(traverse(root)\)在执行的过程中，可以保证每次调用它们时都满足“此时的\(s\)从栈顶开始是此时的\(n\)由近到远所有的祖先”；

结合(a1)(a2)可知，只要构造出满足性质(a1)的\(getFirst(n,s), getSuccessor(n,s)\)，改造后的\(traverse(root)\)就能等价实现原来的算法。而构造这样的\(getFirst(n,s), getSuccessor(n,s)\)实际非常简单，只要把改造前的函数中“关于\(parent\)指针的操作”等效替换成“关于栈\(s\)的操作”，最后保证函数返回时的\(s\)和返回的节点的关系符合(a1)即可。这里直接给出改造后的中序遍历的\(getFirst,getSuccessor\)如下，其中\(s[top]\)表示\(s\)的栈顶：

1) \(getFirst(n,s)\)：开始迭代，每轮迭代若\(n.left\)非空则\(s.push(n)\)然后置\(n=n.left\)并继续迭代，否则退出迭代返回\(n\)；

2) \(getSuccessor(n,s)\)：若\(n.right\)非空则\(s.push(n)\)然后返回\(getFirst(n.right,s)\)。否则开始迭代，每轮迭代“若\(s\)为空则退出迭代返回空，否则若\(s[top].left=n\)则退出迭代返回\(s.pop()\)，否则置\(n=s.pop()\)并继续迭代”；

相应的前序遍历的\(getFirst,getSuccessor\)如下：

1) \(getFirst(n,s)\)：返回\(n\)；

2) \(getSuccessor(n,s)\)：若\(n.left\)非空则\(s.push(n)\)后返回\(n.left\)。否则若\(n.right\)非空则\(s.push(n)\)后返回\(n.right\)。否则开始迭代，每轮迭代“若\(s\)为空则退出迭代返回空，否则若\(s[top].left=n\)且\(s[top].right\)非空则退出迭代返回\(s[top].right\)，否则置\(n=s.pop()\)并继续迭代”；

相应的后序遍历的\(getFirst,getSuccessor\)如下：

1) \(getFirst(n,s)\)：开始迭代，每轮迭代若\(n.left\)非空则\(s.push(n)\)然后置\(n=n.left\)并继续迭代，否则若\(n.right\)非空则\(s.push(n)\)然后置\(n=n.right\)并继续迭代，否则退出迭代返回\(n\)；

2) \(getSuccessor(n,s)\)：若\(s\)为空则返回空。否则若\(s[top].right=n\)则返回\(s.pop()\)。否则若\(s[top].right\)为空则返回\(s.pop()\)。否则返回\(getFirst(s[top].right,s)\)；

由于改造前后的逻辑等价，且替换后的操作与原操作的代价相同，故两者代价相同。由于任何时刻\(s\)都不存储同层(level)节点，故额外空间(\(s\)的大小)总以二叉树深度\(O(h)\)为上界。对于存储\(parent\)指针的二叉树，该指针是二叉树的一部分，故不计入额外空间，但其相比普通二叉树确实多占了\(O(n)\)的空间，故改造后空间复杂度更优。改造后的算法程序如下。

# 中序遍历

def getFirst(node, stack):
    while node.left:
        stack.append(node)
        node = node.left
    return node
 
def getSuccessor(node, stack):
    if node.right:
        stack.append(node)
        return getFirst(node.right, stack)
    while stack:
        if stack[-1].left is node:
            return stack.pop()
        node = stack.pop()
    return None
 
def traverse(root):
    if not root:
        return
    stack = []
    head = getFirst(root, stack)
    while head:
        print(head) # 遍历位置
        head = getSuccessor(head, stack)

# 中序遍历

def getFirst(node, stack):

while node.left:

stack.append(node)

node = node.left

return node

def getSuccessor(node, stack):

if node.right:

stack.append(node)

return getFirst(node.right, stack)

while stack:

if stack[-1].left is node:

return stack.pop()

node = stack.pop()

return None

def traverse(root):

if not root:

return

stack = []

head = getFirst(root, stack)

while head:

print(head) # 遍历位置

head = getSuccessor(head, stack)

# 前序遍历
 
def getFirst(node, stack):
    return node
 
def getSuccessor(node, stack):
    if node.left:
        stack.append(node)
        return node.left
    if node.right:
        stack.append(node)
        return node.right
    while stack:
        if stack[-1].left is node and stack[-1].right:
            return stack[-1].right
        node = stack.pop()
    return None
 
def traverse(root):
    if not root:
        return
    stack = []
    head = getFirst(root, stack)
    while head:
        print(head) # 遍历位置
        head = getSuccessor(head, stack)

# 前序遍历

def getFirst(node, stack):

return node

def getSuccessor(node, stack):

if node.left:

stack.append(node)

return node.left

if node.right:

stack.append(node)

return node.right

while stack:

if stack[-1].left is node and stack[-1].right:

return stack[-1].right

node = stack.pop()

return None

def traverse(root):

if not root:

return

stack = []

head = getFirst(root, stack)

while head:

print(head) # 遍历位置

head = getSuccessor(head, stack)

# 后序遍历
 
def getFirst(node, stack):
    while node.left or node.right:
        stack.append(node)
        node = node.left if node.left else node.right
    return node
 
def getSuccessor(node, stack):
    if not stack:
        return None
    if stack[-1].right is node:
        return stack.pop()
    if not stack[-1].right:
        return stack.pop()
    return getFirst(stack[-1].right, stack)
 
def traverse(root):
    if not root:
        return
    stack = []
    head = getFirst(root, stack)
    while head:
        print(head) # 遍历位置
        head = getSuccessor(head, stack)

# 后序遍历

def getFirst(node, stack):

while node.left or node.right:

stack.append(node)

node = node.left if node.left else node.right

return node

def getSuccessor(node, stack):

if not stack:

return None

if stack[-1].right is node:

return stack.pop()

if not stack[-1].right:

return stack.pop()

return getFirst(stack[-1].right, stack)

def traverse(root):

if not root:

return

stack = []

head = getFirst(root, stack)

while head:

print(head) # 遍历位置

head = getSuccessor(head, stack)

优化基于栈的遍历算法

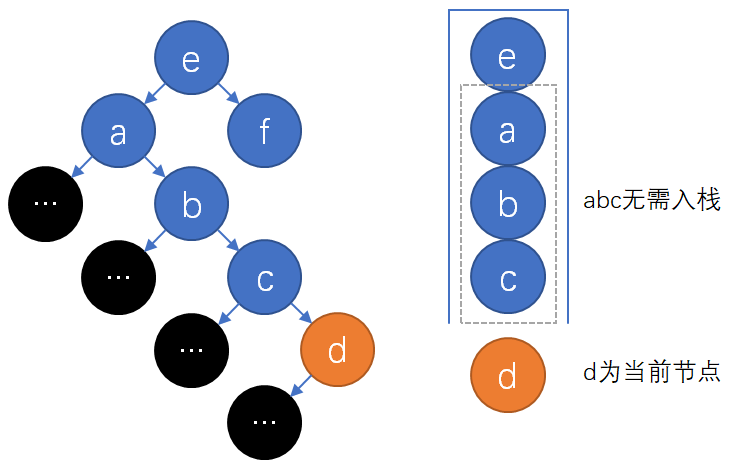
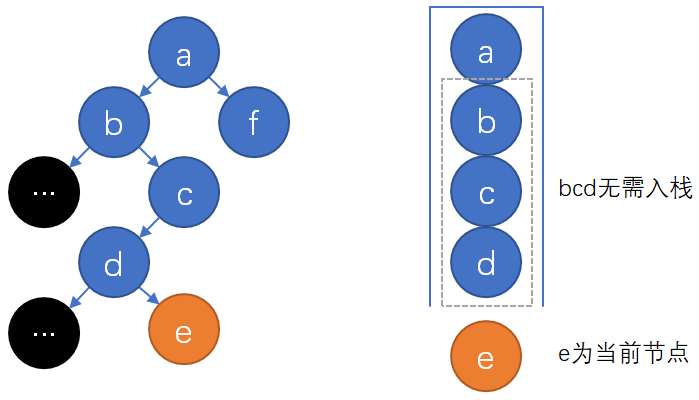
上图第一张给出了优化上述中序遍历的思想。先给出优化中序遍历的方法，对于整个算法仅需修改\(getSuccessor\)：

1) \(*getSuccessor(n, s)\)：若\(n.right\)非空则返回\(getFirst(n.right, s)\)。否则若\(s\)非空则返回\(s.pop()\)。否则返回空；

下面验证优化的正确性，先用\(P[X]\)表示“\(P[X]\)是距\(X\)最近的\(X\)的祖先，且\(X\)在\(P[X]\)左子树。无符合要求的\(P[X]\)时为空”。根据之前对节点前驱后继的讨论，节点\(x\)无右孩子时\(P[x]\)是\(x\)的中序后继(\(P[x]\)为空则无中序后继)，而该优化的核心是根据\(P[X]\)改变\(s\)的意义，精简\(s\)的大小。容易验证优化后的算法中\(getFirst(n, s),*getSuccessor(n, s)\)满足如下新性质：

b1) \(getFirst(n,s), *getSuccessor(n,s)\)若在调用开始时\(s\)从栈顶开始依次是\(P[n],P[P[n]]…\)，则该次调用的返回节点(计为\(n’\))与改造前的函数相同，且该次调用返回时\(s\)从栈顶开始依次是\(P[n’],P[P[n’]]…\)(如果\(P[x]\)为空或\(P[x]\)无意义，实际并不会存入栈中，这里只是为了书写方便)；

\(traverse(root)\)在创建完空栈\(s\)后执行\(head=getFirst(root,s)\)，此时满足\(s\)从栈顶开始依次是\(P[root],P[P[root]]…\)。由于\(traverse\)本身只是一个“外层框架”，所以参考前面的性质(a2)，很容易得到如下的性质：

b2) \(traverse(root)\)每次调用\(getFirst(n,s), *getSuccessor(n,s)\)时都满足\(s\)从栈顶开始依次是\(P[n],P[P[n]]…\)(如果\(P[x]\)为空或\(P[x]\)无意义，实际并不会存入栈中，这里只是为了书写方便)；

结合(b1)(b2)可知优化后的算法能正确实现中序遍历。由于该算法是遍历算法所以代价仍是\(O(n)\)，对于只有左孩子的二叉树，算法执行时栈的大小最大时为\(O(h)\)，所以这种优化不足以得到更优的渐进(大O记号)代价和额外空间。

上图第二张给出了优化前序遍历的思想，其和中序遍历的优化相似，对于整个算法同样仅需修改\(getSuccessor\)：

1) *\(getSuccessor(n, s)\)：若\(n.left\)非空且\(n.right\)非空则\(s\)入栈\(n\)后返回\(n.left\)。否则若\(n.left\)非空则返回\(n.left\)。否则若\(n.right\)非空则返回\(n.right\)。否则若\(s\)非空则返回\(s.pop().right\)。否则返回空；

下面验证优化的正确性，先用\(P'[X]\)表示““\(P'[X]\)是距节点\(X\)最近的\(X\)的祖先，且\(X\)在\(P'[X]\)左子树，且\(P'[X]\)的右孩子非空，无符合要求的\(P'[X]\)时为空”，根据之前对前驱后继的讨论，节点\(x\)无孩子时\(P'[x].right\)是\(x\)的前序后继(\(P'[x]\)为空则无前序后继，\(P'[x]\)非空则\(P'[x].right\)非空)，易验证优化后的算法中\(getFirst(n, s),*getSuccessor(n, s)\)满足如下新性质：

c1) \(getFirst(n,s), *getSuccessor(n,s)\)若在调用开始时\(s\)从栈顶开始依次是\(P'[n],P'[P'[n]]…\)，则该次调用的返回节点(计为\(n’\))与改造前的函数相同，且该次调用返回时\(s\)从栈顶开始依次是\(P'[n’],P'[P'[n’]]…\)(如果\(P'[x]\)为空或\(P'[x]\)无意义，实际并不会存入栈中，这里只是为了书写方便)；

c2) \(traverse(root)\)每次调用\(getFirst(n,s), *getSuccessor(n,s)\)时都满足\(s\)从栈顶开始依次是\(P'[n],P'[P'[n]]…\)(如果\(P'[x]\)为空或\(P'[x]\)无意义，实际并不会存入栈中，这里只是为了书写方便)；

结合(b1)(b2)可知优化后的算法能正确实现前序遍历。由于该算法是遍历算法所以代价仍是\(O(n)\)，对于所有节点的右子树都仅含0~1个节点的二叉树，算法执行时栈的大小最大为\(O(h)\)，所以这种优化不足以得到更优的渐进代价和额外空间。

最后分析后序遍历，注意到后序遍历中所有的“被出栈节点”都会被执行“访问”，不会有直接丢弃“被出栈节点”的情况，所以后序遍历无法按同样的思路仅需优化。不过对于这种后序遍历实现，同个节点至多只入栈1次，而Leetcode官方给出的后序遍历则可能入栈同个节点2次，所以这种实现也不是很差。给出优化后的中序遍历与前序遍历的程序如下。

# 优化后的中序遍历
 
def getFirst(node, stack):
    while node.left:
        stack.append(node)
        node = node.left
    return node
 
def getSuccessor(node, stack):
    if node.right:
        return getFirst(node.right, stack)
    if stack:
        return stack.pop()
    return None
 
def traverse(root):
    if not root:
        return
    stack = []
    head = getFirst(root, stack)
    while head:
        print(head) # 遍历位置
        head = getSuccessor(head, stack)

# 优化后的中序遍历

def getFirst(node, stack):

while node.left:

stack.append(node)

node = node.left

return node

def getSuccessor(node, stack):

if node.right:

return getFirst(node.right, stack)

if stack:

return stack.pop()

return None

def traverse(root):

if not root:

return

stack = []

head = getFirst(root, stack)

while head:

print(head) # 遍历位置

head = getSuccessor(head, stack)

# 优化后的前序遍历
 
def getFirst(node, stack):
    return node
 
def getSuccessor(node, stack):
    if node.left and node.right:
        stack.append(node)
        return node.left
    if node.left:
        return node.left
    if node.right:
        return node.right
    if stack:
        return stack.pop().right
    return None
 
def traverse(root):
    if not root:
        return
    stack = []
    head = getFirst(root, stack)
    while head:
        print(head) # 遍历位置
        head = getSuccessor(head, stack)

# 优化后的前序遍历

def getFirst(node, stack):

return node

def getSuccessor(node, stack):

if node.left and node.right:

stack.append(node)

return node.left

if node.left:

return node.left

if node.right:

return node.right

if stack:

return stack.pop().right

return None

def traverse(root):

if not root:

return

stack = []

head = getFirst(root, stack)

while head:

print(head) # 遍历位置

head = getSuccessor(head, stack)

发表评论 取消回复

发表评论取消回复