用MORRIS方法实现二叉树的迭代遍历

中序遍历的Morris算法

1968年Knuth在其著作TAOCP提出问题：“如何在不用额外空间、不在节点额外存储信息(比如像线索二叉树那样存储额外变量)的前提下\(O(n)\)的实现二叉树中序遍历”。只存储\(O(1)\)规模的“额外信息”是无法保证完成中序遍历的，比如对于所有节点都无右孩子的二叉树，中序遍历“访问”完其最左节点时，此刻算法必须要额外记录了该节点的所有祖先才能保证剩下的遍历过程的正确执行，而其祖先的数目是\(O(n)=O(h)\)，即最坏需\(O(n)\)规模的“额外信息”，所以该问题的难点在于如何存储这些信息。

1979年J.H.Morris在《Traversing Binary Trees Simply and Cheaply》中提出符合Knuth要求的中序遍历算法，算法执行时会动态将二叉树部分空右孩子指针指向其他节点，以临时记录遍历所需的“额外信息”，并在算法结束时还原二叉树。1988年的文章《Morris’ Tree Traversal Algorithm Reconsidered》证明了该算法的正确性，证明思路是先给出种基于栈的中序遍历算法(称为算法A)，然后证明Morris算法在执行过程中临时用空右孩子指针所记录的信息与算法A中的栈所记录的信息等价。本文会借鉴这个思路来构造和证明Morris算法，由于这样得到的算法和原版有些区别，所以标题里称之为“方法”而非“算法”。

下面先给出算法所需的几个关键运算，并说明其意义：

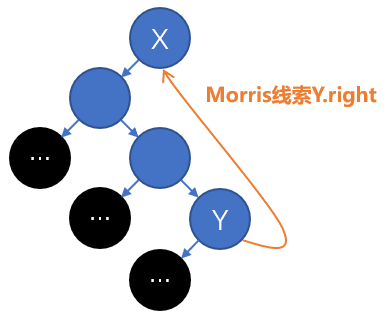
1) \(threading(n)\)：具体步骤是“置\(x=n\)，再置\(n=n.left\)。然后开始迭代，每轮迭代若\(n.right\)非空则置\(n=n.right\)，否则退出迭代。最后置\(n.right=x\)”。其具体意义是将\(n\)的左子树的最右节点的空右孩子指针指向\(n\)，具体如上图第1张所示，根据二叉树性质这个指针一定是空的，须注意到执行\(threading(n)\)时必须保证\(n\)的左子树非空。为方便将\(threading(n)\)执行后修改的右孩子指针称为关于\(n\)的Morris线索，那么执行\(threading(n)\)的作用是建立关于\(n\)的Morris线索，当然其执行前要保证\(n\)有非空的左子树且目前二叉树上没有关于\(n\)的Morris线索。

2) \(isThreaded(n)\)：具体步骤是“置\(x=n\)，再置\(n=n.left\)。然后开始迭代，每轮迭代若\(n\)为空则退出迭代返回假，否则若\(n.right\)存在且\(n.right=x\)则退出迭代返回真，否则置\(n=n.right\)继续迭代”。其具体作用是判断目前二叉树上是否有关于\(n\)的Morris线索，其执行前无需保证\(n\)有非空的左子树。

在给出Morris中序遍历算法前，先回顾之前文章讨论过的“优化后的基于栈的中序遍历算法”，事实上该算法的栈与Morris线索维护的信息等价，所以这里考虑将该算法“转化”成Morris算法如下，灰体字表示“转化后的步骤”以方便对照：

1) \(getFirst(n)\)：开始迭代，每轮迭代若\(n.left\)非空则\(threading(n)\)然后置\(n=n.left\)继续迭代，否则退出迭代返回\(n\)；

2) \(getSuccessor(n)\)：若\(n.right\)存在且\(isThreaded(n.right)\)为假则返回\(getFirst(n.right)\)。否则若\(n.right\)存在则“置\(x=n.right\)，然后置\(n.right\)为空，最后返回\(x\)”。否则返回空；

3) \(traverse(root)\)：若树根\(root\)为空则直接返回，否则执行\(head=getFirst(root)\)，然后“访问”\(head\)，然后开始迭代，每轮迭代执行\(head=getSuccessor(head)\)，执行完后若\(head\)非空则“访问”\(head\)，否则返回；

然后分析上述算法的正确性，为方便讨论先引入一些符号和名词，首先沿用之前文章使用过的符号\(P[X]\)表示“\(P[X]\)是原二叉树中(不考虑Morris线索)距\(X\)最近的\(X\)的祖先，且\(X\)在\(P[X]\)左子树。无符合要求的\(P[X]\)时为空”。根据\(P[X]\)的定义和Morris线索的定义可知，只要\(x.right\)是Morris线索则\(x.right=P[x]\)且\(P[x]\)非空，即\(x.right\)是关于\(P[x]\)的Morris线索，并且注意到这个情况下\(P[x]\)就是\(x\)的中序后继。然后定义右可达(right-reachable)的概念，在某时刻若从节点\(x\)仅沿右孩子指针(无论是否为Morris线索)可到达\(y\)，称此刻\(x\)右可达\(y\)。下面通过验证一组命题来验证该算法的正确性：

a1) \(getFirst(n), getSuccessor(n)\)若在调用开始时二叉树上有且仅有关于\(P[n],P[P[n]]…\)的Morris线索，该次调用的返回值\(n’\)与原算法的\(getFirst(n), getSuccessor(n)\)相同，且二叉树上此时有且仅有关于\(P[n’],P[P[n’]]…\)的Morris线索(如果\(x,P[x]\)为空或无意义，并不会有关于它们的Morris线索，这只为书写方便)；

证明：易验证\(getFirst\)符合命题，这里基于此分情况验证\(getSuccessor(n)\)，若\(n.right\)存在且\(isThreaded(n.right)\)为假，说明\(n.right\)是非空的原右孩子，然后会调用并返回\(getFirst(n.right)\)，根据符号\(P\)的定义，关于\(P[n],P[P[n]]…\)的Morris线索也就是关于\(P[n.right],P[P[n.right]]…\)的Morris线索，所以调用\(getFirst(n.right)\)时符合命题且返回时同样符合。否则若\(n.right\)存在，说明\(n.right\)是Morris线索，此时\(n.right=P[n]\)且\(P[n]\)非空，然后会“置\(x=n.right\)，然后置\(n.right\)为空，最后返回\(x\)”，相当于返回\(P[n]\)并删掉关于\(P[n]\)的Morris线索，故返回时符合命题。否则说明\(n.right\)是空的原右孩子且不是Morris线索，根据题设此时\(P[n]\)为空，可确定\(n\)无中序后继，返回空符合命题。综上命题正确。

a2) 遍历过程中每次调用\(getFirst(n), getSuccessor(n)\)时都满足二叉树上有且仅有关于\(P[n],P[P[n]]…\)的Morris线索(如果\(x,P[x]\)为空或无意义，并不会有关于它们的Morris线索，这只为书写方便)；

证明：只需验证遍历最开始时首次调用\(getFirst(root)\)时符合命题即可，其他情况由(a1)保证，由于\(root\)无祖先，所以\(P[root],P[P[root]]…\)都不存在，而遍历最开始时二叉树上没有Morris线索，所以该命题也是正确的。

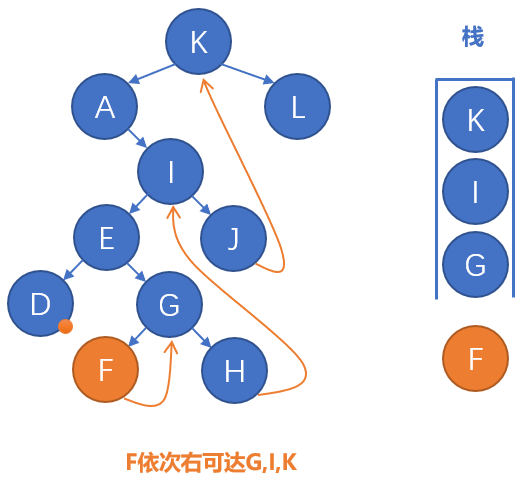
根据上面的命题和其证明过程可发现，原算法中的栈在新算法中以右可达序列的子序列的形式存在，具体例子如上图第2张。最后分析新算法的代价，注意到新算法中包含\(threading\)和\(isThreaded\)调用，其代价是大于\(O(1)\)的，但可以证明整个遍历过程中所有\(threading,isThreaded\)调用的总代价都以\(O(n)\)为上界。根据\(getFirst\)中的迭代步骤可知，遍历中所有的\(getFirst\)调用的迭代过程都不会“途径”同个节点1次以上，否则会导致某2次\(getFirst\)调用返回相同的值，导致遍历算法错误，所以可确定每次\(threading(x)\)传入的\(x\)都不同，进而根据\(threading\)中的迭代步骤可知，遍历中所有\(threading\)调用的迭代过程都不会“途径”同个节点1次以上，否则会导致某2次对不同节点的\(threading\)调用修改同一个右孩子指针，这种情况是不会出现的。所以整个遍历过程中所有\(threading\)调用的总代价是\(O(n)\)。同样每次\(getSuccessor(x)\)调用传入的\(x\)都不同，\(x.right\)非空时会执行\(isThreaded(x.right)\)，注意到\(x.right\)可能是Morris线索，在2次\(getSuccessor(x_1),getSuccessor(x_2)\)调用中可能对同个节点\(y\)执行\(isThreaded(y)\)，\(x_1.right,x_2.right\)当时都指向\(y\)，其中一个是Morris线索，另一个是原二叉树的指针，但仍可确定同个节点至多被执行2次\(isThreaded\)，因为Morris线索所使用的右孩子指针在任何时候都是固定的。由于\(isThreaded\)的迭代步骤和\(threading\)很相似，所以容易确定所有\(isThreaded\)调用的迭代过程都不会“途径”同个节点2次以上，所以整个遍历过程中所有\(isThreaded\)调用的总代价是\(O(n)\)。结合原算法的代价可知新算法的代价也是\(O(n)\)，但其包含更大的常数项，而新算法的额外空间占用则显然是\(O(1)\)。下面直接给出具体的程序实现。

前后序遍历的Morris算法

按上文的“转化基于栈的算法”的思路容易得到前序遍历的Morris算法，但难以直接得到后序遍历的Morris算法，这里换种思路，先找一种能将中序遍历转化成前后序遍历的“通用方法”，再用该方法将中序遍历的Morris算法转化成前后序遍历。

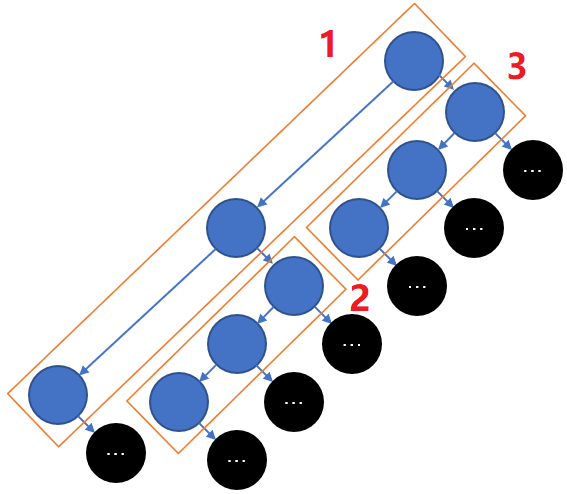
先把二叉树看成由多个“左链表”构成的结构(如上图第1张)，然后在遍历时记录算法首次访问每个“左链表”的时机，那么可发现中序和前序遍历会按相同次序首次访问每个“左链表”，只不过中序遍历访问的是“表尾”节点，而前序遍历访问的是“表头”节点，比如对于上图第1张中的1、2、3号“左链表”，中序和前序遍历都是依次首先访问1、2、3号“左链表”。另外前序遍历还有个特性，其只有在从“表头”开始依次访问完某个“左链表”的所有节点后，才会去访问下一个“左链表”。这些性质本身不难验证，这里不去证明它们，根据这些性质可得到一种将中序遍历转化为前序遍历的方法如下：

b1) 若在中序遍历首次访问每个“左链表”时都顺序打印该“左链表”，则打印结果是前序序列；

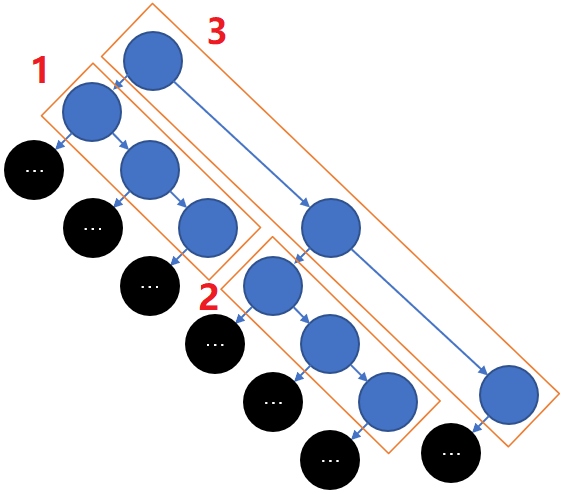
然后把二叉树看成由多个“右链表”构成的结构(如上图第2张)，然后在遍历时记录算法访问每个“右链表”中的最后1个未访问节点的时机，那么可发现中序和后序遍历会按相同次序访问每个“右链表”中的最后1个未访问节点，只不过中序遍历访问的是“表尾”节点，而后序遍历访问的是“表头”节点，比如对于上图第2张中的1、2、3号“右链表”，中序和后序遍历都是依次访问1、2、3号“右链表”中的最后1个未访问节点。另外后序遍历还有个特性，其只有在从“表尾”开始依次逆序访问完某个“右链表”的所有节点后，才会去访问下一个“右链表”。同样根据这些性质可得到一种将中序遍历转化为后序遍历的方法如下：

b2) 若在中序遍历访问每个“右链表”中的最后1个未访问节点时都逆序打印该“右链表”，则打印结果是后序序列；

考虑利用(b1)将中序遍历的Morris算法转化为前序遍历。中序遍历的Morris算法在遍历时访问的节点要么是开始时对树根执行\(getFirst\)返回的节点，要么是\(getSuccessor\)中的\(getFirst\)返回的节点，要么是\(getSuccessor\)本身返回的节点。对于第1种情况，由于树根无父亲，故树根显然是某“左链表”的“表头”，该次\(getFirst\)返回的显然是该“左链表”的“表尾”。对于第2种情况，其是对\(getSuccessor(x)\)中的\(x\)在原二叉树的右孩子\(x.right\)执行\(getFirst\)，\(x.right\)显然是某“左链表”的表头，该次\(getFirst\)返回的显然是该“左链表”的表尾。对于第3种情况，\(getSuccessor(x)\)是直接返回此时的Morris线索\(x.right\)，根据Morris线索的定义\(x.right\)在原二叉树一定有非空的左孩子，所以这种情况返回的节点一定不是某个“左链表”的表尾。综合这3种情况可知遍历过程中的所有\(getFirst\)调用所返回的节点恰好是所有“左链表”的“表尾”节点，且传入的\(x\)是这些“左链表”的“表头”。考虑到中序遍历每次访问“左链表”的“表尾”时都是首次访问该“左链表”，于是可得如下转化方法：

c1) 若在中序遍历的Morris算法每次执行\(getFirst(x)\)的开始时刻顺序打印以\(x\)为“表头”的“左链表”，则打印结果是前序序列；

考虑利用(b2)将中序遍历的Morris算法转化为后序遍历。根据中序遍历的Morris算法的流程可知每个被访问完的节点\(x\)接着都会被执行\(getSuccessor(x)\)，在执行时若\(x.right\)指向原二叉树中\(x\)的右孩子，那\(x\)显然不是某“右链表”的“表尾”，若\(x.right\)是Morris线索，那\(x\)一定是某“右链表”的“表尾”，\(x.right.left\)则显然是该“右链表”的“表头”，若\(x.right\)为空，\(x\)也一定是某“右链表”的“表尾”，根据上文中的命题(a1)可知\(x\)的所有祖先都是右孩子节点或树根，换句话说该“右链表”的“表头”刚好是树根。考虑到中序遍历每次访问“右链表”的“表尾”时都是在访问该“右链表”中最后1个未访问节点，于是可得如下转化方法：

c2) 在中序遍历的Morris算法每次执行到\(getSuccessor(x)\)时，若\(x.right\)为Morris线索，则在\(getSuccessor(x)\)调用结束返回时(将返回值计为\(y\)，此时\(x.right\)这个Morris线索已经被还原为空)逆序打印以\(y.left\)为“表头”的“右链表”，若\(x.right\)为空，则在\(getSuccessor(x)\)调用结束返回时逆序打印以树根为“表头”的“右链表”。那么整体打印结果是后序序列；

分析根据(c1)(c2)得到的算法的代价，(c1)(c2)多出来的打印“左/右链表”的总代价显然是\(O(n)\)，故这部分代价并不会使转化后的算法的代价增大。注意到(c2)的链表打印是逆序的，实现逆序打印要避免占用额外空间，因为Morris算法追求\(O(1)\)的额外空间占用。实现\(O(1)\)额外空间的链表逆序打印可通过“先反转链表，再顺序打印反转后的链表，最后把链表反转回来”的步骤实现。综上根据(c1)和(c2)得到的算法的代价是\(O(n)\)，额外空间为\(O(1)\)。下面给出程序实现，算法的其他细节见程序和注释。