线索二叉树(Threaded Binary Tree)
在孩子表示法二叉树中,任何节点的左右孩子指针都可能为空,事实上总空指针数目满足如下规律:
a) 设任意的孩子表示法二叉树有\(n\)个节点,该二叉树的空指针数目为\(n+1\);
证明:设度为0,1,2的节点数为\(n_0,n_1,n_2\),则空指针总数为\(x=2n_0+n_1\)。之前讨论二叉树性质时证明了\(n_0=n_2+1\)。由于二叉树节点数\(n=n_0+n_1+n_2\),那么\(n=2n_0+n_1-1\),所以\(x=n+1\)。
上述性质表明二叉树有大量空指针,若让空指针指向其他节点以记录额外信息,就能得到线索二叉树。线索二叉树节点需额外维护2个变量描述指针是否表示孩子,这里计为\(leftType,rightType\)。\(leftType=0\)表示指向原左孩子,\(leftType=1\)表示指向其他节点,此时的左孩子指针称为线索,\(rightType\)同理。将普通二叉树变成线索二叉树的过程称为线索化。一般来说线索二叉树特指“用线索记录节点在遍历序列前驱后继的线索二叉树”,所以本文讨论中/前/后序线索二叉树。中/前/后序线索二叉树可按如下方式通过原二叉树来定义,其中\(x\)是“原二叉树”任意节点:
1) 若\(x.left\)为空则置\(x.leftType=1\)并置\(x.left\)为\(x\)的中/前/后序前驱(无前驱指向空),否则置\(x.leftType=0\);
2) 若\(x.right\)为空则置\(x.rightType=1\)并置\(x.right\)为\(x\)的中/前/后序后继(无后继指向空),否则置\(x.rightType=0\);
先给出线索二叉树节点程序如下,之后要讨论的线索化算法会把“原二叉树节点”转换成这种节点。
1 2 3 4 5 6 | class Node: def __init__(self): self.left = None self.right = None self.leftType = 0 self.rightType = 0 |
中序线索二叉树
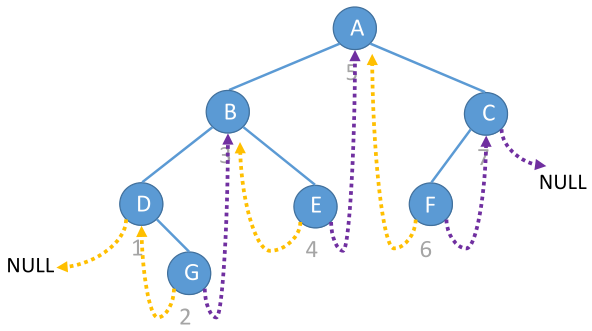
对于任意节点数为\(n>0\)的普通二叉树,其中序序列首节点\(head\)无左子树,末节点\(tail\)无右子树,当\(n=1\)时\(head\)和\(tail\)是同个节点。所以将其中序线索化后,\(head.left\)是空线索,\(tail.right\)是空线索,且其他线索都非空。而根据定义其他非线索指针也都非空。所以中序线索二叉树中除\(head.left\)和\(tail.right\)外无其他空指针。
实现中序线索化算法的思路是以中序遍历算法为框架,在遍历刚“访问”节点(计为\(node\))时确保指针\(prev\)此时指向“上次访问的\(node\)”,进而在中序遍历每次访问的时候,仅通过当前的\(node,prev\)就可以建立线索。需注意的是,在具体实现时要保证这个“一边遍历一边线索化”的过程不影响原本的遍历次序。另外由于中序线索二叉树一般用于实现更高效的中序遍历,所以规定线索化算法要顺便找到\(head,tail\)节点。下面给出中序线索化步骤,设树根为\(root\):
1) 创建全局变量\(prev=null,head=null,tail=null\);
2) 定义递归函数\(F(node)\)如下:
2.1) 若\(node\)为空则退出递归;
2.2) 递归\(F(node.left)\);
2.3) 若\(node.left\)为空则置\(node.leftType=1,node.left=prev\),否则置\(node.leftType=0\);
2.4) 若\(prev\)非空,此时若\(prev.right\)为空则置\(prev.rightType=1,prev.right=node\)否则置\(prev.rightType=0\);
2.5) 若\(prev\)为空则置\(head=node\);
2.6) 置\(prev=node\);
2.7) 递归\(F(node.right)\);
3) 执行\(F(root)\);
4) 若\(prev\)非空则置\(prev.rightType=1\);
5) 置\(tail=prev\);
上述步骤的核心是\(F\),(2.3)到(2.6)对应递归中序遍历的“访问\(node\)的时刻”。(2.3)显然不影响遍历次序,(2.4)仅在\(prev.right\)为空时修改\(prev.right\),若\(prev.right\)为空则说明此时\(prev.right\)的子递归早已直接退出,此时修改\(prev.right\)不影响遍历次序,既然(2.3)(2.4)不影响遍历次序,(2.6)就能在每个“访问\(node\)的时刻”保证\(prev\)指向“上次访问的\(node\)”,步骤(2.5)则单纯用于得到正确的\(head\)。\(F(root)\)结束时\(prev\)指向遍历最后“访问”的节点,其无右子树且右孩子指针未“线索化”,所以额外置\(prev.rightType=1\)。最后置\(tail\)为\(prev\)。其代价和额外空间与递归中序遍历相同。
结合之前文章对“普通二叉树节点的中序前驱后继”的讨论,中序线索二叉树任意节点\(x\)的中序前驱后继满足:
b) 若\(x.right\)非线索则\(x\)的中序后继是\(x\)右子树的中序序列首节点,若\(x.left\)非线索则\(x\)的中序前驱是\(x\)左子树的中序序列末节点。若\(x.right\)为线索则\(x\)的中序后继是\(x.right\)(为空无后继),若\(x.left\)为线索则\(x\)的中序前驱是\(x.left\)(为空无前驱);
基于上述性质和线索化时得到的\(head,tail\),就能通过迭代的寻找\(head\)的中序后继或\(tail\)的中序前驱实现遍历或逆序遍历。之前的文章讨论过普通二叉树如何借助父亲指针实现迭代遍历,而这两种遍历的唯一区别是后者“通过回溯父亲节点找到后继”的分支被替换为“通过线索直接找到后继”,所以该遍历的代价也是\(O(n)\)且隐藏常数更小。逆序遍历与之对称代价相同。中序线索化和基于该线索的中序遍历的程序如下,其中线索化程序输入的二叉树是只有左右孩子指针的普通二叉树,这里利用Python的可动态修改对象的特性直接在节点上加了\(leftType,rightType\)对象属性(变量)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | # 中序线索化 def inThreading(root): prev = head = None def f(node): nonlocal prev,head if not node: return f(node.left) if not node.left: node.leftType = 1 node.left = prev else: node.leftType = 0 if prev: if not prev.right: prev.rightType = 1 prev.right = node else: prev.rightType = 0 else: head = node prev = node f(node.right) f(root) if prev: prev.rightType = 1 return head, prev # 遍历中序线索二叉树 def traverse(head): while head: print(head) # 遍历访问位置 if head.rightType == 1: head = head.right else: head = head.right while head.leftType == 0: head = head.left # 逆序遍历中序线索二叉树 def reverseTraverse(tail): while tail: print(tail) # 遍历访问位置 if tail.leftType == 1: tail = tail.left else: tail = tail.left while tail.rightType == 0: tail = tail.right head, tail = inThreading(root) traverse(head) reverseTraverse(tail) |
前序线索二叉树
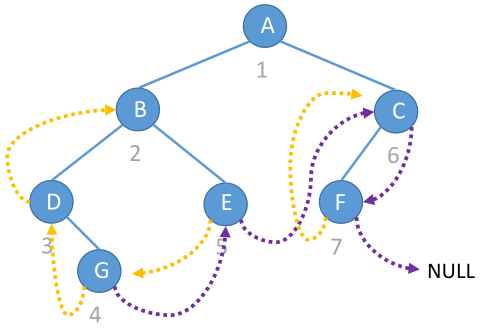
二叉树前序序列首节点\(head\)可能有左子树,末节点\(tail\)一定无右子树。将其前序线索化后,\(head.left\)是空线索当且仅当\(head\)在原二叉树中无左子树,\(tail.right\)是空线索。利用和中序线索化相同的思路,可得前序线索化步骤,设树根为\(root\):
1) 创建全局变量\(prev=null,head=null,tail=null\);
2) 定义递归函数\(F(node)\)如下:
2.1) 若\(node\)为空则退出递归;
2.2) 若\(node.left\)为空则置\(node.leftType=1,node.left=prev\),否则置\(node.leftType=0\);
2.3) 若\(node.right\)为空则置\(node.rightType=1\),否则置\(node.rightType=0\);
2.4) 若\(prev\)非空且\(prev.rightType=1\)则置\(prev.right=node\);
2.5) 置\(prev=node\);
2.6) 若\(node.leftType=0\),则递归\(F(node.left)\);
2.7) 若\(node.rightType=0\),则递归\(F(node.right)\);
3) 执行\(F(root)\);
4) 置\(tail=prev, head=root\);
上述步骤和中序线索化不太一样,因为照搬中序线索化步骤会破坏前序遍历的次序。其分2步完成,第1步的(2.2)和(2.3)是确定\(node\)的左孩子指针是否为线索并确定其指向,确定\(node\)的右孩子指针是否为线索但暂不确定其指向,此时不知道其后继是什么。然后在第2步的(2.4)才确定“上次遍历到的\(node\)”(即当前\(prev\))的右孩子指针的指向。最后(2.6)和(2.7)为避免对线索执行子递归,需预先判断是否为线索,如果是线索则说明对应子树为空,无需递归。另外上述步骤无需像中序线索化那样在递归结束时额外置\(prev.rightType=1\),因为在\(node\)中已经处理过。其代价和额外空间与递归前序遍历相同。
结合之前文章对“普通二叉树节点的前序前驱后继”的讨论,前序线索二叉树任意节点\(x\)的前序前驱后继满足:
c) 若\(x.left\)非线索则\(x\)的前序后继是\(x.left\),否则\(x\)的前序后继是\(x.right\)(无论\(x.right\)是否为线索是否为空)。注意到在\(x.left\)非线索时,寻找\(x\)的前序前驱只能通过回溯\(x\)的父亲节点来完成;
上述性质表明通过线索很容易实现前序遍历,但无法在不借助父亲节点的情况下实现逆序前序遍历,所以前序线索二叉树的逆序前序遍历意义不太大。下面的程序实现了前序线索化和基于该线索的遍历,遍历的代价也是\(O(n)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | # 前序线索化 def preThreading(root): prev = None def f(node): nonlocal prev if not node: return if not node.left: node.leftType = 1 node.left = prev else: node.leftType = 0 if not node.right: node.rightType = 1 else: node.rightType = 0 if prev and prev.rightType == 1: prev.right = node prev = node if node.leftType == 0: f(node.left) if node.rightType == 0: f(node.right) f(root) return root, prev # 遍历前序线索二叉树 def traverse(head): while head: print(head) # 遍历访问位置 if head.leftType == 0: head = head.left else: head = head.right head, tail = preThreading(root) traverse(head) |
后序线索二叉树
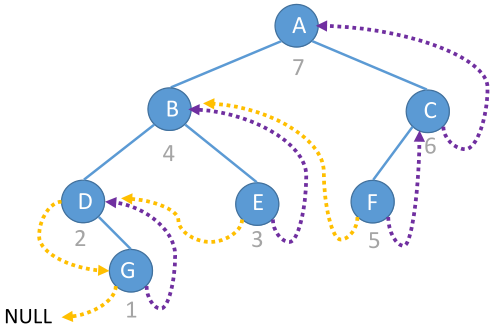
二叉树后序序列首节点\(head\)一定无左子树,末节点\(tail\)可能有右子树。将其后序线索化后,\(head.left\)是空线索,\(tail.right\)是空线索当且仅当\(tail\)在原二叉树中无右子树。利用和前序线索化相同的思路,可得后序线索化步骤,设树根为\(root\):
1) 创建全局变量\(prev=null,head=null,tail=null\);
2) 定义递归函数\(F(node)\)如下:
2.1) 若\(node\)为空则退出递归;
2.2) 递归\(F(node.left)\);
2.3) 递归\(F(node.right)\);
2.4) 若\(node.left\)为空则置\(node.leftType=1,node.left=prev\),否则置\(node.leftType=0\);
2.5) 若\(node.right\)为空则置\(node.rightType=1\),否则置\(node.rightType=0\);
2.6) 若\(prev\)非空且\(prev.rightType=1\)则置\(prev.right=node\);
2.7) 若\(prev\)为空则置\(head=node\);
2.8) 置\(prev=node\);
3) 执行\(F(root)\);
4) 置\(tail=root\);
上述步骤基本照搬了前序线索化的步骤,由于递归左右孩子在“访问当前节点”前发生,故递归前无需像前序线索化那样先做判断。多出来的步骤(2.7)用于将\(head\)指向后序序列的首节点。
结合之前文章对“普通二叉树节点的后序前驱后继”的讨论,后序线索二叉树任意节点\(x\)的后序前驱后继满足:
d) 若\(x.right\)非线索则\(x\)的后序前驱是\(x.left\),否则\(x\)的后序前驱是\(x.left\)(无论\(x.left\)是否为线索是否为空)。注意到在\(x.right\)非线索时,寻找\(x\)的后序后继只能通过回溯\(x\)的父亲节点来完成;
上述性质表明后序线索和前序线索存在对称性,通过线索很容实现逆序后序遍历,但无法在不借助父亲节点的情况下实现正序后序遍历,所以其正序后序遍历也意义不太大。下面给出相关程序实现,遍历的代价也是\(O(n)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | # 后序线索化 def postThreading(root): prev = head = None def f(node): nonlocal prev, head if not node: return f(node.left) f(node.right) if not node.left: node.leftType = 1 node.left = prev else: node.leftType = 0 if not node.right: node.rightType = 1 else: node.rightType = 0 if prev and prev.rightType == 1: prev.right = node if not prev: head = node prev = node f(root) return head, root # 逆序遍历后序线索二叉树 def reverseTraverse(tail): while tail: print(tail) # 遍历访问位置 if tail.rightType == 0: tail = tail.right else: tail = tail.left head, tail = postThreading(root) reverseTraverse(tail) |