堆与二叉堆

堆(Heap)

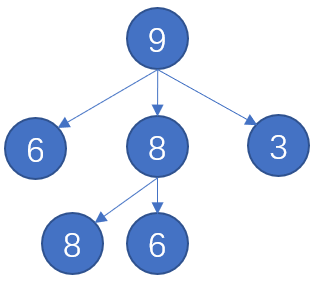
堆也是种基于树的数据结构，整体上分为小根堆(min-heap)和大根堆(max-heap)。如果一个树中的每个节点都包含一个关键字，并且每个节点的关键字都不大于其所有后代的关键字，则称该树是一个小根堆，反之如果每个节点的关键字都不小于其所有后代的关键字，则称该树是一个大根堆。上图给出了一个大根堆的例子。考虑到之后会讨论一些使用到小根堆的算法，并且小根堆和大根堆在各个方面都高度对称，所以之后主要讨论小根堆，并默认堆是指小根堆。

堆和平衡树一样存在很多不同的实现，堆的实现通常比平衡树简单，但也更灵活多变，不同的堆会用到不同的树的表示。事实上之前讨论过的Treap数据结构就使用到了堆，其在同一个二叉树中维护了一个BST和一个堆。

二叉堆(Binary Heap)

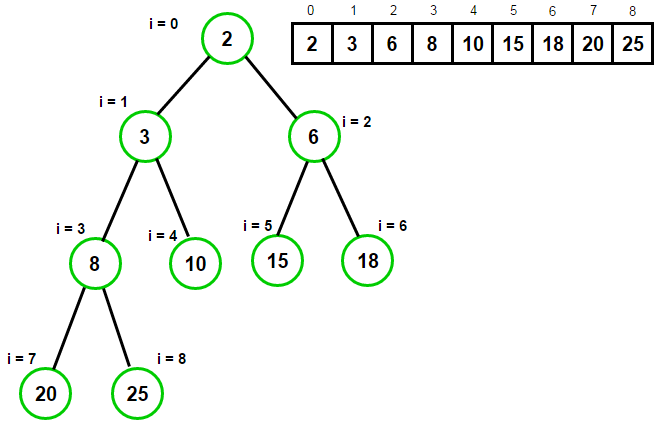
1964年英国学者J. W. J. Williams提出二叉堆，这是种基于完全二叉树的堆。结合之前文章对完全二叉树的讨论，完全二叉树形态与数组长度间存在一一映射，于是一个二叉堆就是一个用数组表示的满足堆性质的完全二叉树，并且这里为了方便描述，约定数组中的每个元素不再是“节点”而是每个关键字\(key\)本身。上图是二叉堆的例子。下面给出二叉堆的一些重要性质：

a1) 设\(a\)是包含\(n>0\)个元素的二叉堆数组，\(0\leq i < n\)是任意整数。如果\(2i+1<n\)则\(a[i]\)有非空的左孩子\(a[2i+1]\)。如果\(2i+2<n\)则\(a[i]\)有非空的右孩子\(a[2i+2]\)。如果\(i\neq 0\)则\(a[i]\)有非空的父亲\(a[\lfloor\frac{i-1}{2}\rfloor]\)；

证明：结合之前文章对完全二叉树的讨论，将原来文章中的“从1计起的序号”换成“从0计起的数组下标”即可。

a2) 设\(a\)是包含\(n>0\)个元素的二叉堆数组。则下标小于\(\lfloor\frac{n}{2}\rfloor\)的元素都是非叶节点，其他元素都是叶节点；

证明：\(n=1\)则无非叶节点，\(n>1\)则\(a[n-1]\)的父亲\(a[\lfloor\frac{n-2}{2}\rfloor]=a[\lfloor\frac{n}{2}\rfloor-1]\)是最末非叶节点。

a3) 设\(a\)是包含\(n>0\)个元素的二叉堆数组，\(0< m \leq n\)是任意整数。则\([a[0],a[1],…,a[m-1]]\)也是二叉堆数组；

证明：显然逆序的去掉二叉堆数组中的元素并不破坏二叉堆的性质。

然后给出二叉堆需要实现的运算如下：

1) \(build(a)\)：称为建堆运算。用于调整任意数值数组\(a\)各个元素的位置以使\(a\)成为二叉堆数组；

2) \(get(a)\)：称为出堆运算。用于从二叉堆数组\(a\)中去掉其中一个最小关键字并返回它；

3) \(put(a, k)\)：称为入堆运算。用于在二叉堆数组\(a\)中插入一个等于\(k\)的关键字；

4) \(decrease(a, i, k)\)：用于将二叉堆数组\(a\)目前位于\(a[i]\)的关键字更新为\(k<a[i]\)；

5) \(sort(a)\)：称为堆排序(heap sort)。用于调整任意数值数组\(a\)各个元素的位置以使\(a\)非严格递减排序；

需明确上述\(get,put,decrease\)结束时须保证数组是二叉堆，\(decrease(a, i, k)\)结束时无需保证原\(a[i]\)在原位置。另外上述部分运算只适用于小根堆，但大根堆运算的功能和实现与之对称，下面不妨给出大根堆运算，但之后并不讨论其具体实现：

1) \(build(a)\)：称为建堆运算。用于调整任意数值数组\(a\)各个元素的位置以使\(a\)成为二叉堆数组；

2) \(get(a)\)：称为出堆运算。用于从二叉堆数组\(a\)中去掉其中一个最大关键字并返回它；

3) \(put(a, k)\)：称为入堆运算。用于在二叉堆数组\(a\)中插入一个等于\(k\)的关键字；

4) \(increase(a, i, k)\)：用于将二叉堆数组\(a\)目前位于\(a[i]\)的关键字更新为\(k>a[i]\)；

5) \(sort(a)\)：称为堆排序(heap sort)。用于调整任意数值数组\(a\)各个元素的位置以使\(a\)非严格递增排序；

二叉堆的运算

上述的部分运算基于\(heapify(a, n, i)\)这个关键操作，其作用的对象是\(a\)的子数组\(a’=[a[0],a[1],…,a[n-1]]\)所对应的完全二叉树，操作结束后\(a'[i]\)位置的子树将满足堆性质。该操作执行的前提首先是\(a’\)和\(a'[i]\)存在，即必须满足\(a\)非空，\(n>0\)且\(n\)不大于\(a\)的元素数，\(0 \leq i < n\)，另外若\(a'[i]\)有左子树则其左子树须满足堆性质，若\(a'[i]\)有右子树则其右子树须满足堆性质。注意到如果\(n\)等于\(a\)的元素数则\(a’=a\)。下面给出\(heapify(a, n, i)\)操作的具体步骤：

1) 初始化\(smallest=i\)；

2) 若\(2i+1 < n\)且\(a[2i+1]<a[smallest]\)，则置\(smallest=2i+1\)；

3) 若\(2i+2 < n\)且\(a[2i+2]<a[smallest]\)，则置\(smallest=2i+2\)；

4) 若\(smallest \neq i\)，则交换\(a[smallest]\)元素和\(a[i]\)元素的位置，然后递归\(heapify(a, n, smallest)\)；

简单验证上述步骤的正确性。假设\(heapify(a, n, i)\)会导致共\(k\)次\(heapify\)调用，然后按照调用次序将传入的\(i\)计为\(i_1…i_k\)。根据上述步骤，显然整个过程结束时\(a'[i_1]…a'[i_k]\)都是它们代表的子树中的最小关键字，并且可确定\(a'[i_k]\)子树必然满足堆性质。另外考虑到整个过程中\(a'[i_2]…a'[i_k]\)的兄弟子树都无变化仍满足堆性质，故\(a'[i_k]…a'[i_i]\)都符合堆性质。

接下来即可在\(heapify\)的基础上给出二叉堆各个运算的具体步骤：

1) \(decrease(a, i, k)\)：首先若\(a[i]\)不存在或\(k>a[i]\)则抛异常。否则置\(a[i]=k\)，然后开始迭代过程。在每轮迭代中首先置\(j=\lfloor\frac{i-1}{2}\rfloor\)，若\(i>0\)并且\(a[i]<a[j]\)，则交换\(a[i]\)与\(a[j]\)的关键字，然后置\(i=j\)并继续迭代。否则退出迭代；

2) \(put(a,k)\)：首先在\(a\)的末尾追加\(+\infty\)并将其下标计为\(i\)，然后通过\(decrease(a, i, k)\)将其更新为\(k\)即可；

3) \(build(a)\)：首先若\(a\)的元素数小于2则直接返回。否则置\(n\)为\(a\)的元素数，然后遍历\(\lfloor\frac{n}{2}\rfloor-1, \lfloor\frac{n}{2}\rfloor-2,…,0\)，并将每轮遍历到的值计为\(i\)，每轮遍历中的步骤都是执行\(heapify(a,n,i)\)；

4) \(get(a)\)：首先若\(a\)为空则抛异常。否则置\(n\)为\(a\)的元素数，然后交换\(a[0]\)与\(a[n-1]\)的关键字，接着置\(k=a[n-1]\)并去从\(a\)中去掉\(a[n-1]\)。此时若\(a\)非空，则执行\(heapify(a,n-1,0)\)。最后返回\(k\)；

5) \(sort(a)\)：首先若\(a\)的元素数小于2则直接返回。否则执行\(build(a)\)，然后遍历\(0,1,…,n-2\)，并将每轮遍历到的值计为\(i\)，每轮遍历中的步骤都是先交换\(a[0]\)与\(a[n-1-i]\)的关键字，然后执行\(heapify(a,n-1-i,0)\)；

简单验证\(build,sort\)的正确性，其他运算显然都正确。对于\(build(a)\)，首先\(a\)中叶节点代表的子树都满足堆性质，\(build(a)\)会按照倒序去\(heapify\)每个非叶节点，故每次\(heapify\)都符合其执行前提，最后\(heapify\)完\(a[0]\)后整个\(a\)满足堆性质。对于\(sort(a)\)，其执行完\(build(a)\)后相当于多次执行\(get\)，并且其通过改变传入\(heapify\)的下标使\(get\)的返回值留在\(a\)内部。通过\(build\)和\(get\)则无法在\(a\)的内部原地完成排序，所以\(sort\)这样的算法也被称为原地算法(in-place algorithm)。

二叉堆的时间复杂度

这里通过一组命题来说明上述各个运算的代价：

b1) 设\(a\)是包含\(n > 0\)个元素的二叉堆数组。则\(decrease(a, i, k)\)、\(put(a,k)\)、\(get(a)\)的代价上界都是\(O(\lg{n})\)；

证明：显然它们的代价上界都是树高\(O(h)\)。而根据之前文章对完全二叉树的讨论\(h=\lfloor\log_2n\rfloor + 1 \leq \log_2n+1\)。

b2) 设\(a\)是包含\(n > 0\)个元素的二叉堆数组。则\(build(a)\)的代价上界是\(O(n)\)；

证明：首先将\(a\)对应的二叉树的高度计为\(h\)，根据二叉树的性质，其中的第\(i>0\)层至多包含\(2^{i-1}\)个节点，并且对其中第\(i\)层的任意节点执行\(heapify\)所产生的递归轮数小于\(h-i+1\)，所以\(build(a)\)的一个代价上界为\(T(n)=\sum_{i=1}^{h}{(h-i+1)2^{i-1}}\)。通过错位相减法可得\(T(n)=2T(n)-T(n)=-h+(\sum_{i=1}^{h-1}{2^i})+2^h=2^{h+1}-h-2<2^{2+\log_2{n}}=O(n)\)。

b3) 设\(a\)是包含\(n > 0\)个元素的二叉堆数组。则\(sort(a)\)的代价上界是\(O(n\lg{n})\)；

证明：其代价相当于1次\(build\)和\(n\)次\(get\)的总代价，所以容易得到其上界为\(O(n+n\lg{n})=O(n\lg{n})\)。

需要注意到如果不进行上述的分析，则很容易认为\(build\)运算的代价上界是不够准确的\(O(n\lg{n})\)。实际上早期的\(build\)运算确实曾是另一种\(O(n\lg{n})\)代价的自顶向下算法，而目前的这种自底向上算法被称为Floyd建堆算法。

总结与实现

下面是二叉堆的程序实现，这里并未将二叉堆实现为对象，而是实现了提供二叉堆运算的类方法。