遍历算法
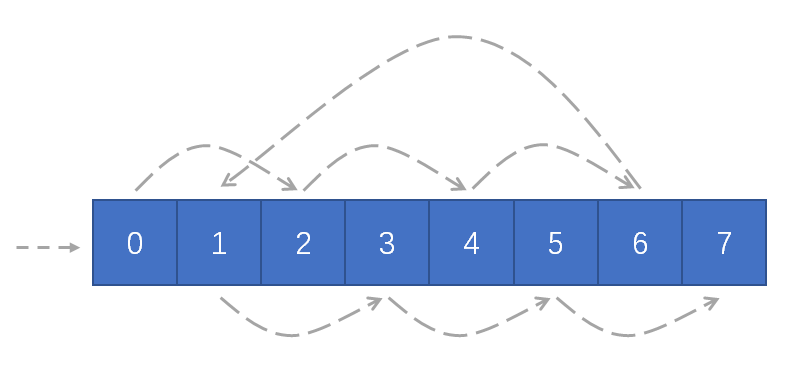
之前在讨论线性表时,用遍历指代“按该线性表的序依次访问所有元素(节点)”,并未详细定义什么是“遍历”。这是因为线性表的遍历通常都是按线性表本身的序来遍历的,并且在日常编程中不太区分遍历、循环、枚举等概念。准确来说遍历(Traversal)是一类特定的算法,其能够按算法设计者所要求的次序,访问且仅访问一次数据结构中的所有元素。比如对于数组,遍历既能是简单的顺序遍历,也可以是更复杂的“先访问全部偶数索引、再访问全部奇数索引”,具体如上图。
对于大部分简单且常见的遍历算法,代价通常都是\(O(n)\)且仅需\(O(1)\)额外空间。但在遇到复杂的数据结构、或需要复杂的访问次序时,可能会有更高的代价和空间复杂度,比如之后会讨论的图遍历。原因之一是当元素间的关系更复杂时,会无法避免的多次“物理访问”同个节点,这时“仅访问一次”的要求就成了“负担”,需要额外的步骤或空间才能区分“仅访问一次”。
二叉树的遍历
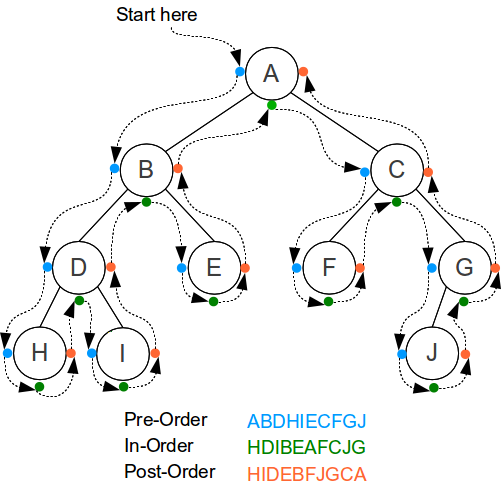
有四种重要的遍历次序会用于二叉树,它们常用于实现更高级的算法。给出这些次序的定义如下:
1) 层次遍历(Level-Order):“从左到右”的依次访问第1层、第2层、…… 的所有节点;
2) 前序遍历(Pre-Order):若树非空,先访问树根,再递归的前序遍历各个子树;
3) 后序遍历(Post-Order):若树非空,先递归的后序遍历各个子树,再访问树根;
4) 中序遍历(In-Order):若树非空,先递归的中序遍历左子树,再访问树根,最后递归的中序遍历右子树;
根据定义方式的不同上述遍历次序可分两类,第一类是用“迭代”方式定义的(第1种),第二类是用递归定义的(第2~4种),除此之外,这两类遍历的访问次序也存在共性,所以分别称为:
1) 广度优先遍历:总是先访问完所有距树根“更近”的节点后才访问“更远”的;
2) 深度优先遍历:总是访问完子树全部节点后才开始访问该子树其他未被访问的兄弟子树;
一般二叉树是有序的,对于广度优先遍历,每个节点的左孩子必须排在右孩子的“左侧”,对于深度优先遍历必须先递归左孩子再递归右孩子。深度优先遍历这种递归定义容易直接转化为递归程序,广度优先遍历可借助队列实现,具体步骤如下:
1) 初始化仅包含树根的队列\(q\);
2) 若\(q\)非空,则出队节点\(node\),否则算法结束。
3) 访问节点\(node\)(完成遍历算法中的“访问且仅访问一次”);
4) 按序将\(node\)的所有孩子入队\(q\),最后返回(2);
分析上述4种遍历的时间复杂度和额外空间复杂度,将二叉树节点总数计为\(n\)。将算法分两类进行分析:
1) 广度优先遍历:各节点仅出入队1次,代价是\(O(n)\)。根据算法流程,额外空间由队列节点数决定,队列最大节点数由最多节点的1~2层决定。根据完美二叉树性质,其最末层节点数\(m\)最多,并满足\(n=2m-1\),这是一种\(O(n)\)额外空间的情况,显然队列不会有\(n\)个以上的节点,所以最坏额外空间就是\(O(n)\),最好则是二叉树退化成线性表时的\(O(1)\);
2) 深度优先遍历:每个节点仅递归1次,且在递归中,除执行子递归,其他步骤的代价是\(O(1)\),所以整体代价是\(O(n)\)。在递归中,虽然没使用队列那样的额外空间,但如果在算法的某一时刻,未结束的子递归数目不是常数而是\(f(n)\),那么每个子递归即使只占\(O(1)\)额外空间,总额外空间也会累加至\(O(f(n))\)。根据递归流程,设树深度为\(h\),同时刻未结束的递归最多有\(O(h)\)个。\(h=n-1\)出现在二叉树退化为线性表时,而完全二叉树是节点数相同时深度最小的,满足\(h=\lfloor\log_2n\rfloor + 1\)。所以最好的额外空间和最坏的额外空间分别是\(O(\lg{n})\)和\(O(n)\);
下面是四种遍历算法在孩子表示法二叉树上的实现,用print来占位表示“访问且仅访问一次”的时机。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | ''' 二叉树的孩子表示法 class TreeNode: def __init__(self): self.left = None self.right = None ''' # 二叉树的层次遍历(广度优先遍历) def levelOrder(root): from collections import deque q = deque([ root ]) while q: node = q.popleft() print(node) # 访问位置 if node.left: q.append(node.left) if node.right: q.append(node.right) # 二叉树的深度优先遍历 def f(root): if root: print(root) # 前序遍历的访问位置 f(root.left) print(root) # 中序遍历的访问位置 f(root.right) print(root) # 后序遍历的访问位置 |
二叉树的遍历序列
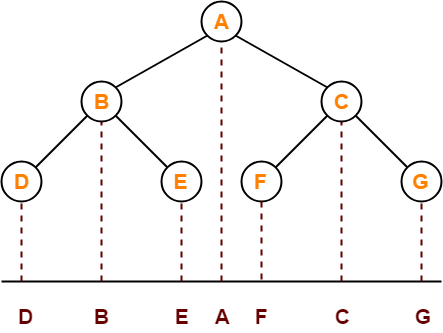

遍历时记录节点被访问的次序可得遍历序列,称为前序序列、中序序列等。其中中序序列最直观,如上图所示节点在水平轴的“投影”就是中序序列。上图也给出3种深度优先遍历序列的节点分布,可发现前后序序列存在对称性,若把后序遍历改成“先递归右子树”的,再把这样得到的遍历序列反转,其刚好就是前序序列。该特性也可通过遍历的递归定义直接验证,只不过要从“逆序”的角度看,对于修改过的后序遍历,倒数第1步是访问树根,倒数第2步是递归左子树,倒数第3步是递归右子树。展开这个递归过程,倒数第1步是访问树根(倒数第1),倒数第2步是递归左子树,递归左子树时,倒数第3步是访问左孩子(倒数第2)…….刚好是倒过来的前序遍历。层次序列则显得和它们都不同,因为定义的差别比较大。
对于节点数超过1的任何二叉树而言。前后序序列不同,因为树根位置不同。前中序序列相同当且仅当所有节点都无左孩子,后中序序列相同当且仅当所有节点都无右孩子,可通过遍历的递归定义直接验证。层次后序序列不同,因为树根位置不同。层次中序序列相同当且仅当所有节点都无左孩子,可通过对比二者的定义验证。层次前序序列相同当且仅当“所有节点无右孩子”或“所有节点的左子树仅含0或1个节点”,可通过对比二者的定义验证。
仅通过一种遍历序列无法唯一确定原二叉树(节点数大于1),同个遍历序列能对应多个不同的二叉树,这是一般性结论:
a) 设二叉树节点数为\(n>0\),对于任意二叉树遍历算法,若遍历次序与节点本身的特性无关(仅与树形态有关),则对于任意遍历序列,存在\(C(n)\)个不相同的二叉树与之对应,且这些二叉树形态不同。其中\(C(n)\)为第\(n\)个卡特兰数;
证明:之前文章中证明过,节点数\(n\)对应\(C(n)\)种二叉树形态。由于该遍历算法仅与二叉树形态有关,所以对于每种二叉树形态,算法访问“放节点的位置”的次序是固定的,只要根据这个“次序”在相应的“位置”放入遍历序列的各节点就能构造出1个树,一共能构造\(C(n)\)个,它们之间的形态不同,所以一定是互不相同的。
用遍历序列重建二叉树
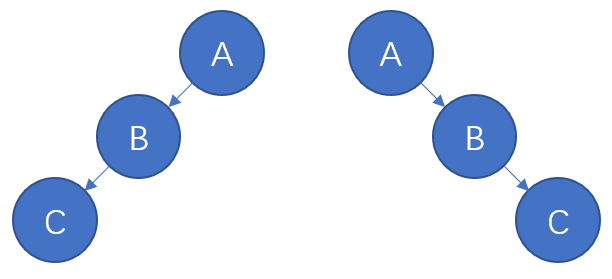
对于访问次序与节点本身特性无关的遍历算法,其遍历序列无法唯一的“还原”二叉树。但使用多种这样的遍历算法,得到多种遍历序列,最少仅需2种序列就能唯一“还原”二叉树。比如同时给定中序和前序序列,或同时给定中序和后序序列。这里以前者为例讨论其“还原”二叉树的步骤,对于后者同理。具体的递归步骤如下:
1) 若两序列长度为0或1:则该树为空或仅有1个树根;
2) 若两序列长度大于1:先确定树根为前序序列第1个元素,那么在中序序列中树根左边是“左子树的中序序列”,右边是“右子树的中序序列”。再根据2个序列中的元素将前序序列划为“左子树的前序序列”和“右子树的前序序列”,这时找到2对“中序和前序序列”,2对序列的最大长度为\(n-1\)也可能这2对都为空。最后对这2对“中序和前序序列”递归;
上述步骤无论得到怎样的“左右子树划分”都没有歧义,递归中的每个子递归都有定义。
前序和后序序列使用上述方法时会有“歧义”,比如上图2个二叉树的前序和后序序列都是ABC和CBA,这里分析“歧义”的成因,第一步是确定树根,然后发现其前序序列第2个元素是B,后序序列倒数第2个元素也是B,根据2种遍历序列的特征,可确定左或右子树为空,所以BC和CB分别是左或右子树的前序与后序序列,它们作为左或右子树的遍历序列都可行,这就产生了“歧义”。换句话说仅当二叉树每个节点都满足“没有孩子或有2个孩子”才能被前序和后序序列唯一确定,这种二叉树为满二叉树(Full Binary Tree)。还原满二叉树的递归步骤如下,该步骤能“发现”非满二叉树并停止程序:
1) 若两序列长度为0或1:则该树为空或仅有1个树根;
2) 若两序列长度大于1:先确定树根为前序序列第1个元素(后序序列倒数第1个元素),然后分情况讨论:
2.1) 若前序序列第2个元素是后序序列倒数第2个元素:结束整个步骤并“报告”该树非满二叉树;
2.2) 若前序序列第2个元素不是后序序列倒数第2个元素:前序序列第2个元素是左子树的树根,后序序列倒数第2个元素是右子树的树根。利用这2个树根和这2种序列的特征,可以划分1对“左子树的前序序列”和“左子树的后序序列”、1对“右子树的前序序列”和“右子树的后序序列”,最后对这2对“前序和后序序列”递归;
上述步骤每次递归都“还原”一个节点,如某次递归进入(2.1)说明这个节点只有1个孩子,整个递归如从从未进入(2.1)说明所有节点都“有2个或0个孩子”,即满二叉树,那么整个步骤正常结束时就能“还原”整个二叉树。
层次和前序序列、层次和后序序列都无法唯一“还原”二叉树,上图刚好也是例子。但层次和中序序列可唯一“还原”二叉树,与前面讨论过的遍历序列不同,子树的“子层次序列”不是层次序列中连续的一段,这里给出相关性质:
b) 设二叉树层次序列为\(L\),其任意后代(看做树)的层次序列为\(L’\)。\(L’\)的元素次序和\(L\)中这部分元素的次序相同;
c) 设二叉树层次序列为\(L\),其任意后代(看做树)的中序序列为\(L’\)。取\(L’\)所有元素在\(L\)的索引,索引最小的元素即该后代;
证明:取该后代(看做树)的层次序列\(L{”}\),取\(L’\)所有元素在\(L{”}\)的索引,根据层次序列性质,索引最小的元素显然是该后代。根据上面的(b),仅看属于\(L’\)的这部分节点,在\(L{”}\)索引最小的节点也是在\(L\)索引最小的节点。
根据上述性质,可得到利用层次和中序序列“还原”二叉树的递归步骤如下:
1) 若两序列长度为0或1:则该树为空或仅有1个树根;
2) 若两序列长度大于1:从中序序列找到其在层次序列索引最小的元素(树根)。然后中序序列树根左边是“左子树的中序序列”,右边是“右子树的中序序列”。对“左子树的中序序列”和原层次序列递归、“右子树的中序序列”和“原层次序列”递归;
在程序实现上述步骤时,会经常遇到“找序列A的某元素在序列B的位置”,这可以借助哈希表避免遍历查找,否则时间复杂度可能变大。另外为方便程序实现,可认为遍历序列的元素都是“节点的唯一标识(唯一的数字或字符串)”而非“节点对象本身”,程序建立二叉树时让节点带“唯一标识”表示其对应原遍历序列的“节点”即可。具体递归实现如下,每个程序都用Python的dict作哈希表,故额外空间是\(O(n)\)。对于“前序+中序”和“前序+后序”程序,每次递归除执行子递归以外的代价是\(O(1)\),所以整体代价是\(O(n)\)。对于“层次+中序”程序,每次递归需额外遍历“子中序序列”,整体代价是\(O(n^2)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 | ''' 二叉树的孩子表示法 这里的key是节点唯一标识 遍历序列中存放的是各个key而不是节点本身 class TreeNode: def __init__(self, key): self.key = key self.left = None self.right = None ''' # 前序序列+中序序列重建二叉树 def build1(preOrder, inOrder): # 用于反查节点在中序序列的索引,能避免用遍历来查找 inOrderMap = { inOrder[i]:i for i in range(len(inOrder)) } # f(子前序序列起始元素索引,子中序序列起始元素索引,两个子序列的长度) def f(preOrderStart, inOrderStart, size): if size == 0: return None inOrderRootIdx = inOrderMap[preOrder[preOrderStart]] leftSize = inOrderRootIdx - inOrderStart rightSize = size - leftSize - 1 root = TreeNode(preOrder[preOrderStart]) root.left = f(preOrderStart + 1, inOrderStart, leftSize) root.right = f(preOrderStart + 1 + leftSize, inOrderRootIdx + 1, rightSize) return root return f(0, 0, len(inOrder)) # 前序序列+后序序列重建满二叉树 def build2(preOrder, postOrder): postOrderMap = { postOrder[i]:i for i in range(len(postOrder)) } def f(preOrderStart, postOrderStart, size): if size == 0: return None if size == 1: return TreeNode(preOrder[preOrderStart]) if preOrder[preOrderStart + 1] == postOrder[postOrderStart + size - 2]: raise Exception("非满二叉树") # 如果不抛异常依然能还原二叉树,会在节点仅有单个子树时一律当成左子树。 leftRootPostIdx = postOrderMap[preOrder[preOrderStart + 1]] leftSize = leftRootPostIdx + 1 - postOrderStart rightSize = size - leftSize - 1 root = TreeNode(preOrder[preOrderStart]) root.left = f(preOrderStart + 1, postOrderStart, leftSize) root.right = f(preOrderStart + 1 + leftSize, postOrderStart + leftSize, rightSize) return root return f(0, 0, len(postOrder)) # 层次序列+中序序列重建二叉树 def build3(levelOrder, inOrder): levelOrderMap = { levelOrder[i]:i for i in range(len(levelOrder)) } def f(inOrderStart, size): if size == 0: return None # 找子中序序列元素在层次序列的所有索引中最小的索引值 # 这就是子树根在层次序列的索引 # 再利用它找到在子中序序列的索引 levelOrderRootIdx = float('inf') inOrderRootIdx = None for i in range(inOrderStart, inOrderStart + size): if levelOrderMap[inOrder[i]] < levelOrderRootIdx: levelOrderRootIdx = levelOrderMap[inOrder[i]] inOrderRootIdx = i leftSize = inOrderRootIdx - inOrderStart rightSize = size - leftSize - 1 root = TreeNode(inOrder[inOrderRootIdx]) root.left = f(inOrderStart, leftSize) root.right = f(inOrderStart + 1 + leftSize, rightSize) return root return f(0, len(inOrder)) ''' build1( [3,9,20,15,7], [9,3,15,20,7], ) ''' |