队列相关问题

两个栈实现队列

该问题是“有2个空栈$s_1,s_2$，出入栈运算都是$O(1)$代价的，要求用这2个栈实现一个队列，出入队运算都是$O(1)$摊还代价的”。用2个栈实现队列的思路很简单，把一组元素入栈$s_1$再出栈入栈到$s_2$就能把$s_1$的栈底变成$s_2$的栈顶，进而就能实现队头的出队。这里具体来看如何实现，首先对于入队运算，直接入栈$s_1$即可，对于出队运算，当$s_2$为空时把$s_1$的元素全部出栈并依次入栈$s_2$，最后弹出$s_2$的栈顶作为队头出队。当$s_2$非空，直接弹出$s_2$的栈顶作为队头出队即可。

上述过程中，每个元素的入队都是1次$s_1$的入栈，出队都是3次的$s_1$出栈、$s_2$入栈、$s_2$出栈操作。对于$2n$次队列操作，最好的情况是发生$2n$次入队操作，最坏的情况是发生$n$次入队、$n$次出队，对于最坏的情况，也仅意味着发生了$4n$次栈操作。所以此时的总代价是$O(n)$，每次操作的摊还代价是$O(1)$。下面是具体程序实现。

队列的最大值(单调队列算法)

该问题是“实现1个队列，其支持求当前最大值的$max$运算，且出入队和$max$的摊还代价是$O(1)$”。该问题看起来与栈的最值问题类似，但栈每次$pop$后能回到上次$push$前，队列没有该性质，不易找到$O(1)$的$max$实现，但容易找到$O(1)$摊还代价的实现，比如用2个可$O(1)$代价求最大值的栈模拟队列。这里讨论另一种实现，各运算的实现步骤如下：

0) 初始化：创建空的普通队列$q$、空的双端队列$dq$，其中$dq$能查看左右队头；

1) $put(x)$: $x$入队$q$。从右队头循环的出队$dq$若$dq$非空且右队头小于$x$。最后从$dq$右队头入队$x$；

2) $get()$: 从$q$出队，出队元素计为$x$。此时$dq$也非空，若其最左队头等于$x$，则左队头出队1次。最后返回$x$；

3) $max()$：返回$dq$最左端元素；

想要分析上述步骤，必须先明确$dq$的意义，这里通过“命题+证明”讨论。

a) 设队列的$dq = (x_0,x_1…x_n)$有至少1个元素，任意$x_i$都在其$q$中且顺序相同。当$dq$只有1个元素时必须满足$q$中$x_0$前的元素都小于$x_0$。当$dq$多于1个元素时必须满足$x_{i-1} \geq x_i$，且$q$中$x_{i-1},x_i$间的元素都小于$x_i$，$x_0$前的元素都小于$x_0$；

b.1) 对于初始队列($q,dq$为空)或满足(a)的队列，执行1次$put(x)$后满足(a)；

证明：初始队列显然可以。对于非初始队列，若$x > x_0$，$x$成为新$dq$队头，新$dq$只留有$x$这个元素，满足(a)。若$x_n \geq x$，$x$成为新$dq$队尾且不导致任何$dq$元素出队，满足(a)。若$x_{i-1} \geq x > x_i$，$x$会使$dq$中$x_i$和其后面的全部元素出队，并取代$x_i$位置。从$q$的角度看，$x$是其新队尾，而$x_{i-1}$到$x$间的元素全部小于$x$，因为$x$大于原来$dq$中的$x_i,x_{i+1}…x_n$，也满足(a)。

b.2) 对于满足(a)的队列，执行1次$get$后满足(a)或成为初始队列($q,dq$为空)；

证明：设$get$的元素为$x$，若$x$不等于$x_0$，$x$只能是$q$中$x_0$前的元素，$dq$前后无变化，满足(a)。若$x$等于$x_0$，出队的$x$就是$x_0$本身，$q,dq$会同时出队$x_0$，新$dq = (x_1,…x_n)$，新$q$的$x_1$前的元素都是原来$x_0,x_1$间的元素，所以满足(a)。

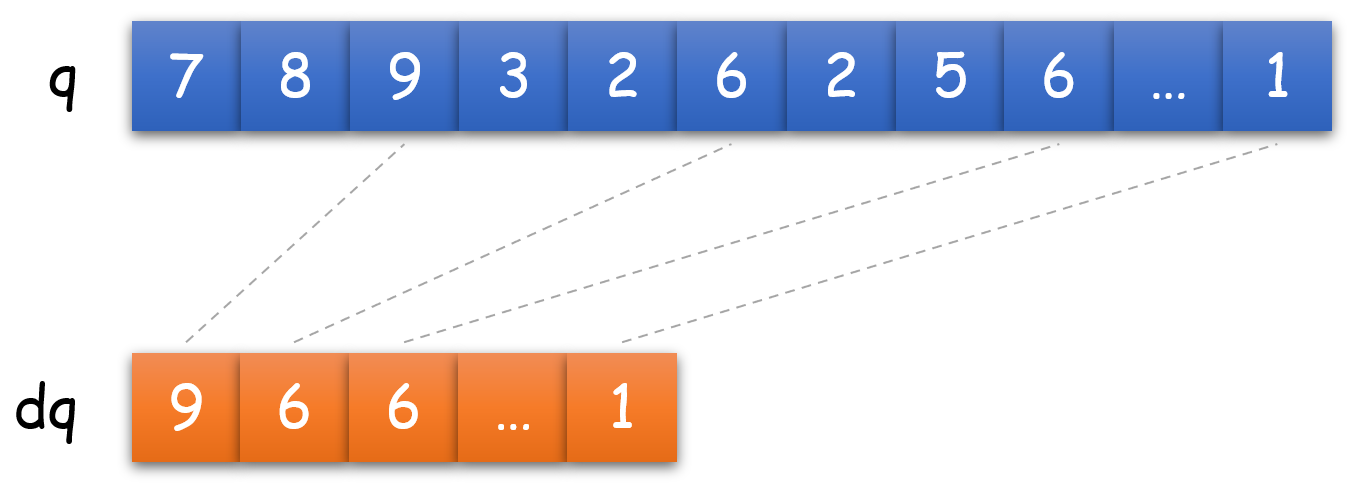
根据(b)的2条结论可以知道，初始化队列后，其经过任意的$get/put$后不是初始队列($q,dq$为空)就是满足(a)的。对于满足(a)的队列，其$dq$的左队头是$dq$中最大的，而$dq$中所有元素都是其在$q$“划分的区间”里的最大值，故$dq$的左队头是$q$中的最大值，进而$max$能正确返回最大值。更直观的可以看上面的图片，该图片是同一个队列中$q,dq$的对比。

在上述队列中，双端队列$dq$中的元素时刻被维护为从左到右单调递减的，这种队列称为单调队列，使用了单调队列的算法称为单调队列算法，是一类比较灵活的队列算法。下面讨论各操作的时间复杂度，设$q,dq$所有运算都是$O(1)$的，那么$max,get$也是$O(1)$的，对于初始队列，如果执行$k$次$put$或$get/put$，则至多有$O(k)$个元素出入队，而每个元素从入队到出队，至多从$q,dq$各出入队1次，故总代价是$O(k)$，摊还代价是$O(1)$。下面是程序实现。

滑动窗口的最大值

该问题是“给定1个数值数组$nums$，1个固定的滑动窗口大小值$k$(窗口容纳的元素数)，其中$k$不大于$nums$的长度，这个滑动窗口会像上图一样从左到右，一次一个元素的滑动。要求从左到右的求出每个窗口的最大值，以数组形式返回”。很多滑动窗口型的问题都可以用队列算法解决，这个问题就可以用前面讨论过的最大值队列/单调队列直接解决。

这里分析下时间复杂度，这时的最大值队列是供另一个算法使用的。设$nums$大小为$n$，最大值队列共执行$n$次$put$和$n-k$次$get$，这时最大值队列的$O(1)$摊还代价就能看作$O(1)$实际代价，总代价是$O(n)$。具体程序如下。