数组相关问题 – JONY'S WORDPRESS

反转数组

该问题是“给定一个数组，将其元素按从右到左重新排列，比如输入\([1,2,3]\)，应该得到\([3,2,1]\)。要求在原数组上反转，且只能占用常数额外空间”。这个问题可通过以中心为对称轴，从最外层开始反转，比如\([1,2,3,4,5]\)，会先变成\([5,2,3,4,1]\)，然后变成\([5,4,3,2,1]\)，两轮即可完成。然后考虑问题的边界，当数组有奇数个元素，两索引最后会在中心元素处相遇，当数组有偶数个元素，两索引最后会出现右边小于左边的情况。所以当右边的索引小于等于左边的索引时就意味着算法结束。该算法的时间复杂度是\(O(n)\)，其中\(n\)为数组中元素的个数。具体程序实现如下。

def reverse(arr):
    i, j = 0, len(arr) - 1
    while i < j:
        arr[i], arr[j] = arr[j], arr[i]
        i += 1
        j -= 1

def reverse(arr):

i, j = 0, len(arr) - 1

while i < j:

arr[i], arr[j] = arr[j], arr[i]

i += 1

j -= 1

旋转数组

该问题是“给定一个数组和整数\(offset\)，想象这个数组首尾连成环，然后顺时针旋转\(offset\)位。比如输入\([1,2,3,4,5]\)和2，应该得到\([4,5,1,2,3]\)，要求原地完成并只占用常数的额外空间”。这个问题最容易想到的是像队列那样，从最右出队\(offset\)次，然后依次入队。但如果\(offset\)和数组元素数同阶，这种实现会导致\(O(n^2)\)的时间复杂度。

考虑用上述反转数组的思路解决，还是以\([1,2,3,4,5]\)为例，第一步想象其根据3,4间的“轴”做镜像，第二步把“轴”左边的\([5,4]\)和右边的\([3,2,1]\)各做一次反转数组，分别得到\([4,5]\)和\([1,2,3]\)，第三步把左右两边拼起来就是\([4,5,1,2,3]\)。然后再看第一步的做镜像，由于这种镜像的结果和“轴”在哪个元素的位置上无关，所以这一步实际就是反转整个数组。最后考虑到\(offset\)在大于数组长度(计为\(l\))时也是有意义的，所以实际\(offset\)应当取\(offset ~\%~ l\)来简化问题。

这种方法用常数次的3次反转数组解决了问题，所以其时间复杂度是\(O(n)\)。具体程序实现如下，这里实现了递归版的反转数组，这样实现旋转数组时，调用起来很简洁清晰。

def _reverse(arr, i, j):
    if i < j:
        arr[i], arr[j] = arr[j], arr[i]
        return _reverse(arr, i+1, j-1)

def rotate(arr, offset):
    if len(arr) > 0:
        offset = offset % len(arr) 
        _reverse(arr, 0, len(arr) - 1)
        _reverse(arr, 0, offset - 1)
        _reverse(arr, offset, len(arr) - 1)

def _reverse(arr, i, j):

if i < j:

arr[i], arr[j] = arr[j], arr[i]

return _reverse(arr, i+1, j-1)

def rotate(arr, offset):

if len(arr) > 0:

offset = offset % len(arr)

_reverse(arr, 0, len(arr) - 1)

_reverse(arr, 0, offset - 1)

_reverse(arr, offset, len(arr) - 1)

合并排序数组

该问题是“给定2个升序排序的数组\(A,B\)，求由\(A,B\)元素组成的升序排序数”。可通过每轮取出2个数组中的最小值，然后追加到结果数组完成。当一个数组为空时把另一数组整个追加到结果数组上来就完成了程序。由于最小值只能是\(A,B\)当前“左端点”中最小的，所以每轮代价可控制在\(O(1)\)，整体代价为\(O(|A|+|B|)\)，具体程序如下。

def f(a,b):

    result = []
    i = j = 0

    while i < len(a) and j < len(b):
        if a[i] < b[j]:
            result.append(a[i])
            i += 1
        else:
            result.append(b[j])
            j += 1

    if i == len(a):
        for k in range(j, len(b)):
            result.append(b[k]) 
        return result

    if j == len(b):
        for k in range(i, len(a)):
            result.append(a[k])
        return result

def f(a,b):

result = []

i = j = 0

while i < len(a) and j < len(b):

if a[i] < b[j]:

result.append(a[i])

i += 1

else:

result.append(b[j])

j += 1

if i == len(a):

for k in range(j, len(b)):

result.append(b[k])

return result

if j == len(b):

for k in range(i, len(a)):

result.append(a[k])

return result

之字遍历二维数组

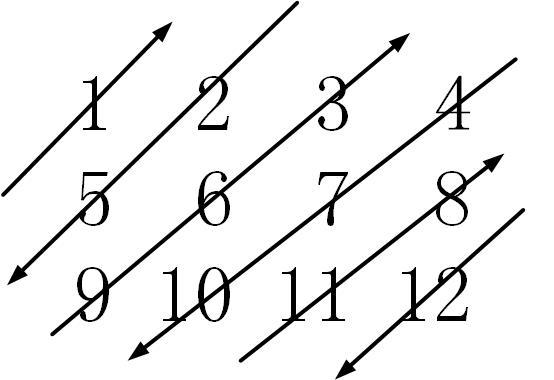
该问题是“给定二维数组形式的\(m\)行\(n\)列矩阵，按之字形遍历元素，具体如上图所示”。遍历方向可分为“向右上”和“向左下”，这里以向右上为例分析，其存在两种边界情况，上面没有更多元素、右面没有更多元素，这时需要顺时针找到下个元素并以此开始一个向左下的新遍历。具体就是上面没有更多元素时，找右边的元素开始新的遍历。右边没有更多元素时，找下边的元素。对于正右上角的元素，其同时符合这2种边界，这时则应该找下面的元素。下面是具体实现。

def f(matrix):

    result = []
    x, y = 0, 0
    direction = 1

    while y < len(matrix) and x < len(matrix[0]):

        result.append(matrix[y][x])

        if direction == 1:
            if x == len(matrix[0]) - 1:
                y += 1
                direction = 2
            elif y == 0:
                x += 1
                direction = 2
            else:
                y -= 1
                x += 1

        else:
            if y == len(matrix) - 1:
                x += 1
                direction = 1
            elif x == 0:
                y += 1
                direction = 1
            else:
                y += 1
                x -= 1

    return result

def f(matrix):

result = []

x, y = 0, 0

direction = 1

while y < len(matrix) and x < len(matrix[0]):

result.append(matrix[y][x])

if direction == 1:

if x == len(matrix[0]) - 1:

y += 1

direction = 2

elif y == 0:

x += 1

direction = 2

else:

y -= 1

x += 1

else:

if y == len(matrix) - 1:

x += 1

direction = 1

elif x == 0:

y += 1

direction = 1

else:

y += 1

x -= 1

return result

螺旋遍历二维数组

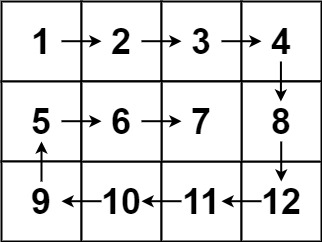
该问题是“给定二维数组形式的\(m\)行\(n\)列矩阵，按顺时针螺旋的方式遍历元素，具体如上图所示”。虽然这个遍历的轨迹是螺旋的，但其次序等价于顺时针从左上角元素遍历第一层外圈，顺时针从左上角元素遍历第二层外圈，顺时针从左上角元素遍历第三层…不过这里的“圈”不一定能是完整的”圈”，有3种边界的情况的“圈”要考虑：

1) 仅有横向一行，遍历到该行最末元素时算法结束；

2) 仅有纵向一列，遍历到该列最末元素时算法结束；

3) 仅有挨着的两行，遍历完第二行时算法结束；

def f(matrix):

    if len(matrix) == 0:
        return []

    yStart, yEnd = 0, len(matrix) - 1
    xStart, xEnd = 0, len(matrix[0]) - 1
    result = []

    while xEnd >= xStart and yEnd >= yStart:

        for i in range(xStart, xEnd + 1):
            result.append(matrix[yStart][i])

        if yStart == yEnd:
            break

        for i in range(yStart + 1, yEnd + 1):
            result.append(matrix[i][xEnd])

        if xStart == xEnd:
            break

        for i in reversed(range(xStart, xEnd)):
            result.append(matrix[yEnd][i])

        if yEnd == yStart + 1:
            break

        for i in reversed(range(yStart + 1, yEnd)):
            result.append(matrix[i][xStart])
        
        xStart += 1
        xEnd -= 1
        yStart += 1
        yEnd -= 1

    return result

def f(matrix):

if len(matrix) == 0:

return []

yStart, yEnd = 0, len(matrix) - 1

xStart, xEnd = 0, len(matrix[0]) - 1

result = []

while xEnd >= xStart and yEnd >= yStart:

for i in range(xStart, xEnd + 1):

result.append(matrix[yStart][i])

if yStart == yEnd:

break

for i in range(yStart + 1, yEnd + 1):

result.append(matrix[i][xEnd])

if xStart == xEnd:

break

for i in reversed(range(xStart, xEnd)):

result.append(matrix[yEnd][i])

if yEnd == yStart + 1:

break

for i in reversed(range(yStart + 1, yEnd)):

result.append(matrix[i][xStart])

xStart += 1

xEnd -= 1

yStart += 1

yEnd -= 1

return result

旋转二维数组

该问题是“给定二维数组形式的正方形矩阵，对其做顺时针90度旋转，要求原地完成并只占常数额外空间”。首先可确定，参考上述解决螺旋遍历的思路，一圈圈的旋转是可以解决的，但这种程序比较繁琐，所以用按对称轴翻转来等效解决。先把当前上行/右列/下行/左列分别计为ABCD，那么旋转后的上行/右列/下行/左列就分别为D’AB’C，撇号表示按“左到右”或“上到下”的次序看，元素排列与原来相反。这里就借这种符号分析如何把ABCD翻转成D’AB’C，具体为依次的2次翻转操作：

1) ABCD按主对角线(从左上角到右下角的对角线)翻转，得到DCBA；

2) DCBA按纵轴翻转，得到D’AB’C；

这2种翻转操作转化为原地完成的程序实现(元素交换)是这样：

1) 按主对角线翻转：把左下(右上)半部分任意元素(可包括对角线元素)计为\(M[y][x]\)，交换\(M[y][x]\)与\(M[x][y]\)；

2) 按纵轴翻转：把左半部分任意元素(可包括纵轴元素)计为\(M[y][x]\)，交换\(M[y][x]\)与\(M[Y-y][x]\)(\(Y\)是最大行序号)；

算法只包含常数次的遍历，所以其时间复杂度是\(O(1)\)。

def f(matrix):

    for y in range(len(matrix)):
        for x in range(y + 1):
            matrix[y][x] , matrix[x][y] = matrix[x][y] , matrix[y][x]

    for l in matrix:
        for x in range(len(l) // 2):
            l[x], l[(len(l)-1) - x] = l[(len(l)-1) - x], l[x]

def f(matrix):

for y in range(len(matrix)):

for x in range(y + 1):

matrix[y][x] , matrix[x][y] = matrix[x][y] , matrix[y][x]

for l in matrix:

for x in range(len(l) // 2):

l[x], l[(len(l)-1) - x] = l[(len(l)-1) - x], l[x]

区间求和(前缀和算法)

该问题是“设计一个结构，其初始化时需要传入一个数组，该结构上有函数能查询该数组下标\(i\)到\(j\)之间(包括\(i,j\))元素的和。这个结构在初始化后会被多次调用其求和函数，所以要求其代价为\(O(1)\)，该结构占用的额外空间不能超过\(O(n)\)”。解决这个问题的方法是构造前缀和数组\(sums\)，其中\(sums[i]\)表示原数组前\(i+1\)个元素的和。当需要求区间和时，只需要从\(sums\)中找两个合适的元素相减即可，具体程序实现如下。这种构造了前缀和数组的算法称为前缀和算法，应用范围很广。

class NumArray(object):

    def __init__(self, nums):
        for i in range(len(nums)):
            if i > 0:
                nums[i] = nums[i] + nums[i - 1]
        self.sums = nums

    def sumRange(self, i, j):
        if i == 0:
            return self.sums[j]
        return self.sums[j] - self.sums[i - 1]

class NumArray(object):

def __init__(self, nums):

for i in range(len(nums)):

if i > 0:

nums[i] = nums[i] + nums[i - 1]

self.sums = nums

def sumRange(self, i, j):

if i == 0:

return self.sums[j]

return self.sums[j] - self.sums[i - 1]

绝对众数(摩尔投票算法)

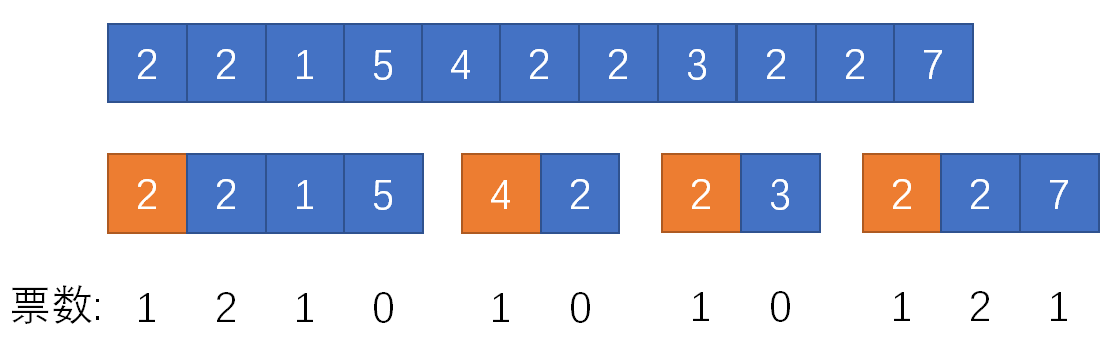
绝对众数是出现次数严格大于其他数出现次数总和的数。求数组绝对众数的经典算法是摩尔投票算法，也叫多数投票算法，于1981年发表，核心思想是“如果给所有数投票，非绝对众数的票加起来都无法超过绝对众数”。算法流程如下：

1) 遍历数组元素并计为\(i\)；

2) 若当前无候选人，则设定候选人为\(i\)并将其票数设为1。回到(1)；

3) 若当前有候选人且候选人是\(i\)，则自增候选人票数。回到(1)；

4) 若当前有候选人且候选人不是\(i\)，则自减候选人票数，若候选人票数减为0则删除候选人。回到(1)；

如上图所示，候选人从“产生”到“消失”都会划分1个“子数组”，子数组的首个元素就是候选人，所有子数组按序拼接就是原数组。除了最后一个子数组，所有其他子数组的元素数都是偶数，且首个数的出现次数刚好是子数组长度的一半。对于最后一个子数组，由于最终的票数不一定刚好归零，所以其首个数的出现次数大于等于子数组长度的一半。

考虑结合上述“子数组”证明：“绝对众数存在时，循环结束时候选人一定存在，且等于绝对众数”。假设遍历结束时候选人刚好被删，这时表明在所有子数组中，首个数的出现次数都刚好是子数组长度的一半，这导致没有任何数的出现次数能超过整个数组长度的一般，导致矛盾。继续假设遍历结束时存在候选人\(x\)且其不等于绝对众数\(y\)，在最后一个子数组中\(y\)一定占不到一半，且\(y\)在其他子数组至多占一半，导致矛盾。所以只有\(y=x\)才可能利用最后一个子数组的“数量优势”超过一半。

注意到当绝对众数不存在时，上述流程算法不保证返回的是出现次数最多的数，容易构造反例验证。但即使不确定绝对众数是否存在，也只需要再次遍历元素并对上述步骤得到的结果计数，如计数结果表明其出现次数不超过一半，说明不存在绝对众数，否则其就是绝对众数。具体程序如下，程序第2个循环块用于判断绝对众数的存在。

def f(nums):

    mode = vote = None
    for i in nums:
        if mode is None:
            mode = i
            vote = 1
        elif i == mode:
            vote += 1
        else:
            vote -= 1
            if vote == 0:
                mode = None

    count = 0
    for i in nums:
        if mode == i:
            count += 1
    if count > len(nums) / 2:
        return mode

def f(nums):

mode = vote = None

for i in nums:

if mode is None:

mode = i

vote = 1

elif i == mode:

vote += 1

else:

vote -= 1

if vote == 0:

mode = None

count = 0

for i in nums:

if mode == i:

count += 1

if count > len(nums) / 2:

return mode

\(\frac{1}{k}\)绝对众数

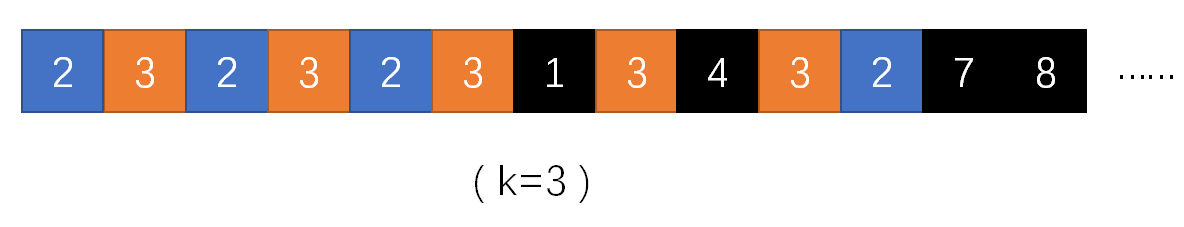
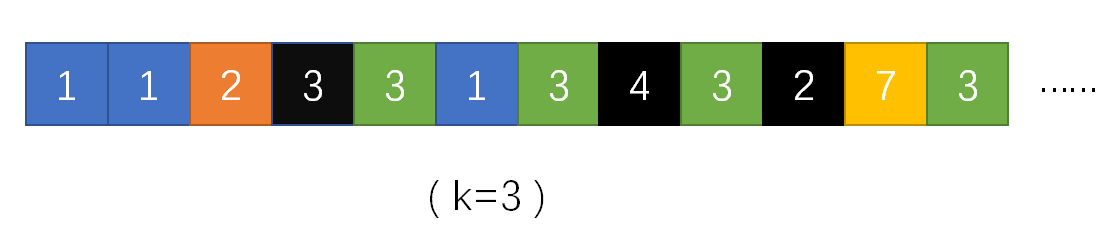
该问题是“求数组出现次数严格大于元素总数\(\frac{1}{k}\)的数”。该问题最多有\(k-1\)个解，最少时无解。前面的摩尔投票算法解决了\(k=2\)时的问题，这时解至多1个。扩展的摩尔投票算法通过把候选人扩展到\(k-1\)个解决该问题。流程如下：

1) 遍历数组\(nums\)的索引\(i\)；

2) 若当前存在等于\(nums[i]\)的候选人，自增该候选人的票数。返回(1)；

3) 若当前候选人总数小于\(k-1\)，创建1个候选人等于\(nums[i]\)，并将其票数初始化为1。返回(1)；

4) 所有候选人票数自减，并删除所有自减后票数归零的候选人。返回(1)；

这里简单归纳下上述步骤的逻辑特征，首先由于步骤(2)先于步骤(3)判断，所以每次循环结束后，候选人间是无重复的。而由于步骤(3)先于步骤(4)判断，所以只有在候选人总数达到\(k-1\)后，才可能进入步骤(4)递减候选人的票数。但这里还不明确各步骤的意义，前面讨论\(k=2\)的摩尔投票时，通过把元素划入多个“子数组”的直观方法分析。对于一般的\(k\)这种方法不适用，但可以使用更一般的“元素分组”分析，而“元素分组”会在\(k=2\)时退化成“子数组”。

a) 若某轮循环有候选人被删，则可确定1个“元素分组”，其包含的元素为\(nums[0],nums[1]…nums[i]\)(\(i\)是该次循环的索引)，再从中去掉属于之前已确定的其他“元素分组”的元素，并按当前循环结束时的候选人票数去掉等于候选人的元素(比如共2个候选人A、B，分别有2、3票。此时要去掉2个A、3个B，相等元素去掉哪个无所谓)。最后一次循环可能不满足(a)的条件，这时认为最后一个“元素分组”是\(nums\)未划入其他分组的元素；

根据上述步骤，每次循环结束后，所有的候选人都互不相等。除了最后一个“元素分组”，每个“元素分组”都包含\(k\)类元素，第\(1,2…k-1\)类分别是值等于候选人\(1,2…k-1\)的元素，第\(k\)类则是值不等于候选人\(1,2…k-1\)的元素。这\(k\)类元素的数目都相等，这说明“元素分组”中任何数的出现次数都不超过分组元素总数的\(\frac{1}{k}\)。上图第1张是\(k=3\)的部分\(nums\)的例子。循环到数字8时候选人是2和3，该轮循环结束时候选人2被删除，3剩1票。上述所有元素去掉任意1个3后得到第1个“元素分组”。上图第2张是另一个例子，第1个元素分组是\(1,2,3\)，第2个是\(1,3,1,3,4,2\)。直观上看，之所以称为“元素分组”而非“子数组”是因为要从“子数组”挖掉若干元素，而这些挖掉的元素又被之后的“元素分组”使用。

b) 遍历结束时，问题的解集是当前候选人集合的1个子集或空集；

上述命题即算法的正确性，证明思路和前面的摩尔投票算法相似，可采用反证法。假设存在解\(x\)不等于遍历结束时的任何候选人，然后把遍历结束时的情况分3种讨论。第1种情况是没有候选人，这时所有“元素分组”都没有出现次数都超过分组元素总数\(\frac{1}{k}\)的数，这时一定无解，导致矛盾。第2种情况是有小于\(k-1\)个候选人，根据上述步骤最后1个“元素分组”只能由候选人组成，\(x\)不在其中。对于所有其他“元素分组”，\(x\)不超过元素总数的\(\frac{1}{k}\)。所以\(x\)在整个数组的出现次数不超过元素总数的\(\frac{1}{k}\)，导致矛盾。第3种情况是有\(k-1\)个候选人，根据上述步骤在最后1个“元素分组”中，\(x\)的出现次数一定小于元素总数的\(\frac{1}{k}\)，最终也导致矛盾。综上任何解都是某个候选人，无候选人则是无解的1个充分条件。

根据(b)可知，遍历结束后，还需要些额外步骤得到完整的解集。具体来说是检查每个候选人的出现次数是否大于数组元素数的\(\frac{1}{k}\)，只要大于就是其中一个解，这样必然能得到完整的解集。下面是程序实现，其使用2个数组分别记录候选人和票数，代价是\(O(kn)\)，额外空间是\(O(k)\)。使用其他非数组结构替换这2个数组，还能把代价继续降到\(O(n)\)。

def f(nums, k):

    vote = [None] * (k - 1)
    mode = [None] * (k - 1)

    for i in nums:
        for j in range(k - 1):
            if mode[j] is not None and mode[j] == i:
                vote[j] += 1
                break
        else:
            for j in range(k - 1):
                if mode[j] is None:
                    mode[j] = i
                    vote[j] = 1
                    break
            else:
                for j in range(k - 1):
                    vote[j] -= 1
                    if vote[j] == 0:
                        mode[j] = None
    
    result = []
    count = [0] * (k - 1)

    for i in nums:
        for j in range(k - 1):
            if mode[j] is not None and mode[j] == i:
                count[j] += 1
    for j in range(k - 1):
        if mode[j] is not None and count[j] > len(nums) / k:
            result.append(mode[j])
            
    return result

def f(nums, k):

vote = [None] * (k - 1)

mode = [None] * (k - 1)

for i in nums:

for j in range(k - 1):

if mode[j] is not None and mode[j] == i:

vote[j] += 1

break

else:

for j in range(k - 1):

if mode[j] is None:

mode[j] = i

vote[j] = 1

break

else:

for j in range(k - 1):

vote[j] -= 1

if vote[j] == 0:

mode[j] = None

result = []

count = [0] * (k - 1)

for i in nums:

for j in range(k - 1):

if mode[j] is not None and mode[j] == i:

count[j] += 1

for j in range(k - 1):

if mode[j] is not None and count[j] > len(nums) / k:

result.append(mode[j])

return result

发表评论 取消回复

发表评论取消回复