汉诺塔问题(Hanoi Tower Problem)
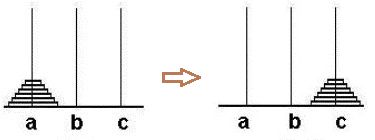
印度有一个古老的传说,在贝拿勒斯的圣庙里,一块黄铜板上插着三根宝石针。印度教主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是汉诺塔(如上图所示)。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭。而梵塔、庙宇和众生也都将同归于尽。
\(k\)层汉诺塔问题可以这样表述:“有\(a,b,c\)三个柱子,其中\(a\)有\(k\)片圆盘,圆盘的大小从上到下严格递增。允许一次移动一个圆盘到其他柱子,每次移动后所有柱子上的圆盘上面不能有更大的圆盘。问如何操作能把所有圆盘移动到\(c\)柱”。这里规定解为序列,序列元素是二元组\((X,Y)\)表示“从\(X\)柱移一片圆盘到\(Y\)柱”,那么解就是有顺序的一系列移动步骤。
找到分治算法的要点在于抽象出问题中的“对称性”,并以此为拆分子问题的切入点:
1) 下方圆盘对上方圆盘“没有干扰”,比如“3层汉诺塔问题”的解可用来解决“如何把5层汉诺塔中的顶上3层移到c柱”;
2) \(a,b,c\)柱的“身份”分别是“起始柱/中转柱/终点柱”,但在拆分子问题时,\(a,b,c\)的“身份”可互换;
然后为了定义清楚“子问题”的结构,用符号\(G(k,X,Y,Z)\)指代“以XYZ为起始柱/中转柱/终点柱的\(k\)层汉诺塔问题”。那么这个问题的可拆分为“先解决子问题\(G(k-1,a,c,b)\),然后把a剩下的最后1个圆盘移动到c,最后解决子问题\(G(k-1,b,a,c)\)”。问题的边界在\(G(1,X,Y,Z)\),此时的解非常简单即“X到Z”。这种定义问题的方式利用了上述(2)的对称性,而能够正确的拆分出子问题\(G(k-1,a,c,b)\)和\(G(k-1,b,a,c)\)是因为上述(1)。下面是程序实现。
1 2 3 4 5 6 7 8 9 10 11 12 | def hanoi(result, k, X, Y, Z): if k == 0: return hanoi(result, k-1, X, Z, Y) result.append([X, Z]) hanoi(result, k-1, Y, X, Z) result = [] hanoi(result, 3, 'a', 'b', 'c') print(result) |
汉诺塔传说最有趣的地方是仅移动64个柱子就毁灭世界,那世界现在还没毁灭是不是因为64个柱子要移动很久?这里分析时间复杂度\(T(k)\),其满足递推关系\(T(k)=2T(k-1) + O(1)\)。主定理没有说怎么解这个递推式,但这个递推式很好直接解出\(T(n)=O(2^k)\),这就是为什么世界还没有毁灭的原因。