比较排序
排序算法(sorting)是一类非常重要的基础算法,高德纳在其著作《计算机程序设计艺术》的第3卷专门讨论排序与查找。排序算法一般被分为比较排序(comparison sort)与非比较排序两类来研究,其中比较排序是通过两两比较元素最终得到排序的算法。在设计实际应用的排序算法时通常会关注如下特性:
1)稳定性:比较结果相等的元素能够保持原本的次序;
2)原地性(in-place):能够在原数据结构上完成排序而不是创建新数据结构存储排序结果;
对于实际应用中的比较排序程序,会根据问题规模选择算法、根据内存限制考虑利用外存、做并行计算(排序网络)等,这里不考虑。排序算法通常会尽量满足如下特性:
1)稳定:相等的元素维持原来的次序;
2)原地排序:在原存储结构(比如数组)上完成排序,而不是用新对象存储结果;
本文讨论几种历史上经典的几种比较排序算法,它们是\(O(n^2)\)或\(O(nlgn)\)时间复杂度的。\(O(n^2)\)算法相对容易找到,可通过类似“遍历\(n\)次,每次都找出剩下元素中最大的”的策略完成。但如果之前没了解过二叉树,则很难想到\(O(nlgn)\)的算法。事实上\(O(nlgn)\)刚好是比较排序的理论时间复杂度极限,这里简单讨论一下:
1) 把问题归纳成:“需要至少多少次两两比较,才能从\(n\)个数的全排列中,找出其中一个正确排列”;
2) 由于元素在各排列分布的对称性,每取2个元素比较(2个元素至少1个未曾参与比较),可筛掉约一半的排列;
3) 比较\(k\)次后大致剩下\(\frac{n!}{2^k}\)个排列,问题化为求不等式\(2^k \geq n!\),取对数后为\(k \geq Clg(n!) \);
4) Stirling公式\(n!\approx \sqrt{2\pi n}\left( \frac{n}{e} \right) ^n\)取对数后有\(O(lg(n!))=O(nlg(n))\),综上可得\(k \geq O(nlg(n))\);
\(O(n^2)\)算法
冒泡排序(可视化:https://visualgo.net/zh/sorting?slide=6 )
1 2 3 4 5 6 7 8 9 | def sort(d): for i in range(len(d)): swapped = False for j in range(len(d)-i-1): if d[j+1]<d[j]: d[j],d[j+1] = d[j+1],d[j] swapped = True if not swapped: break |
选择排序(可视化:https://visualgo.net/zh/sorting?slide=7 )
1 2 3 4 5 6 7 | def sort(d): for j in range(len(d)): idx = j for i in range(j,len(d)): if d[idx]>d[i]: idx = i d[idx],d[j] = d[j],d[idx] |
插入排序(可视化:https://visualgo.net/zh/sorting?slide=8 )
1 2 3 4 5 6 7 | def sort(d): for i in range(len(d)): for j in range(i,0,-1): if d[j] <= d[j-1]: d[j],d[j-1] = d[j-1],d[j] else: break |
上述几种算法都很好理解,时间复杂度直接根据程序的形式就能直接判断。
\(O(nlgn)\)算法
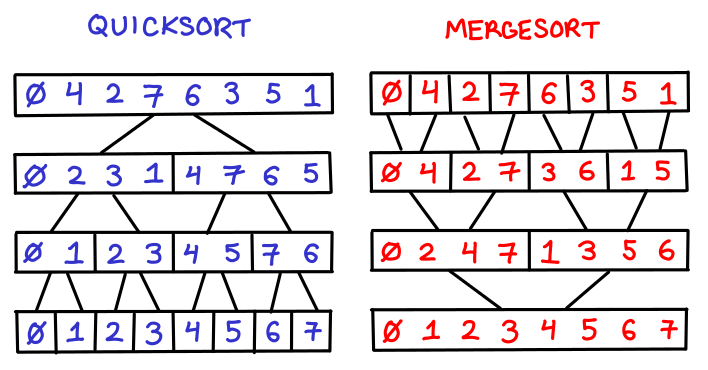
这里讨论2种分治算法,归并排序划分子问题的方式是把当前序列从中间切开,然后递归的求这两个子序列的排序,最后把这两个排好序的子序列整理得到排序。具体的整理方式是这样,循环比较两序列末尾,每次都把最大的拿出来即可,这一步的代价是\(O(n)\)。所以时间复杂度满足递推关系\(T(n) = 2T(\frac{n}{2})+O(n)\),利用主定理可得时间复杂度为\(O(nlgn)\)。
归并排序 (可视化:https://visualgo.net/zh/sorting?slide=10 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def sort(l): if len(l)<2: return l q = int(len(l)/2) left = sort(l[:q]) right = sort(l[q:]) return merge(left,right) def merge(left,right): i,j,result = 0,0,[] while i<len(left) and j<len(right): if left[i]<right[j]: result.append(left[i]) i+=1 else: result.append(right[j]) j+=1 result += left[i:] result += right[j:] return result |
快速排序也是一种分治算法,其每轮递归都是先把序列分成左右两半,其中,右半边的最小元素一定大于等于左半边所有元素。需注意这种策略不能保证左右两半边是“差不多等长”的。这意味着其时间复杂度不能用\(T(n) = 2T(\frac{n}{2})+O(n)\)递推式来描述,并且如果对于一个奇怪的输入,每次递归左右元素数目都差距悬殊,时间复杂度最坏是\(O(n^2)\)。虽然如此,数学上可证明对大量随机的序列做快排,平均每个序列需要的时间是\(O(nlgn)\),这称为算法的平均时间复杂度。
原地快速排序 (可视化:https://visualgo.net/zh/sorting?slide=11 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | def sort(arr): low = 0 high = len(arr) - 1 quickSort(arr, low, high) def quickSort(arr,p,r): if p >= r: return q = partition(arr, p, r) quickSort(arr, p, q-1) quickSort(arr, q+1, r) def partition(arr,p,r): x = arr[r] i = p - 1 for j in range(p,r): if arr[j] <= x: i += 1 arr[i],arr[j] = arr[j],arr[i] arr[i+1],arr[r] = arr[r],arr[i+1] return i+1 |