约瑟夫环问题
传说在古罗马时期,罗马人占领乔塔帕特后,犹太士兵与约瑟夫不愿投降,于是约瑟夫提出一起自杀的方式:“所有人围成圈,从某人开始报数,每报到3该人自杀,然后再由下个人重新报数,直到所有人自杀”。但约瑟夫其实不想自杀,那他站在什么位置才能最后轮到他自杀?这就是约瑟夫环问题,也叫丢手绢问题。问题的解可用士兵编号来表示。
简单的算法是用环形链表模拟过程,但这里讨论复杂一点的分治算法。先用\(G(n,k)\)符号表示“共\(n\)个人,间隔为\(k\)(\(k=1\)表示下个人)的约瑟夫环问题”。对于\(G(n,k)\),第一次士兵自杀后,问题转化为更小规模的\(G(n-1,k)\),求解\(G(n-1,k)\)得到最后自杀的编号后,将其换算为问题\(G(n,k)\)对应的编号即可。进一步定义函数\(F(n,k)\)为“问题\(G(n,k)\)的解,其中士兵编号从0开始”,定义域满足\(n>0,k\geq 0\),其中\(k>n\)也是有意义的。显然有\(F(1,k)=0\)的边界情况。
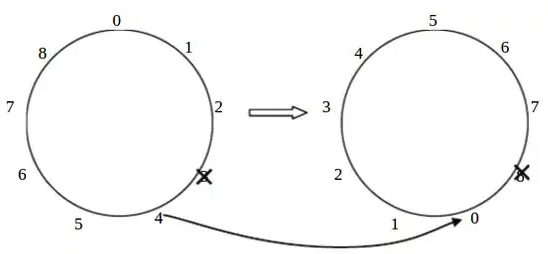
然后来整理函数\(F\)的递推关系,首先对于问题\(G(n,k)\),第一个自杀士兵的下一个士兵的编号是\((k+1)\%n\),这个士兵也是“子问题”中编号为0的士兵。其中的\(\%\)为求余数运算,用于处理\(k\)太大的情况。上图描述了第一个士兵自杀后,\(G(n-1,k)\)子问题中的新士兵编号,通过观察可得关系\(F(n,k) = (F(n-1,k) + (k+1)\%n)\%n\),再次使用\(\%\)也是用来处理编号换算越界的情况。结合\(F\)的边界情况很容易得到其递推程序。这个分治策略刚好能回避已自杀士兵的编号所带来的干扰。
1 2 3 4 | def f(n, k): if n == 1: return 0 return ((k + 1) % n + f(n - 1, k)) % n |
直接观察得出上述算法的时间复杂度是关于总人数的\(O(n)\)。