最小生成树
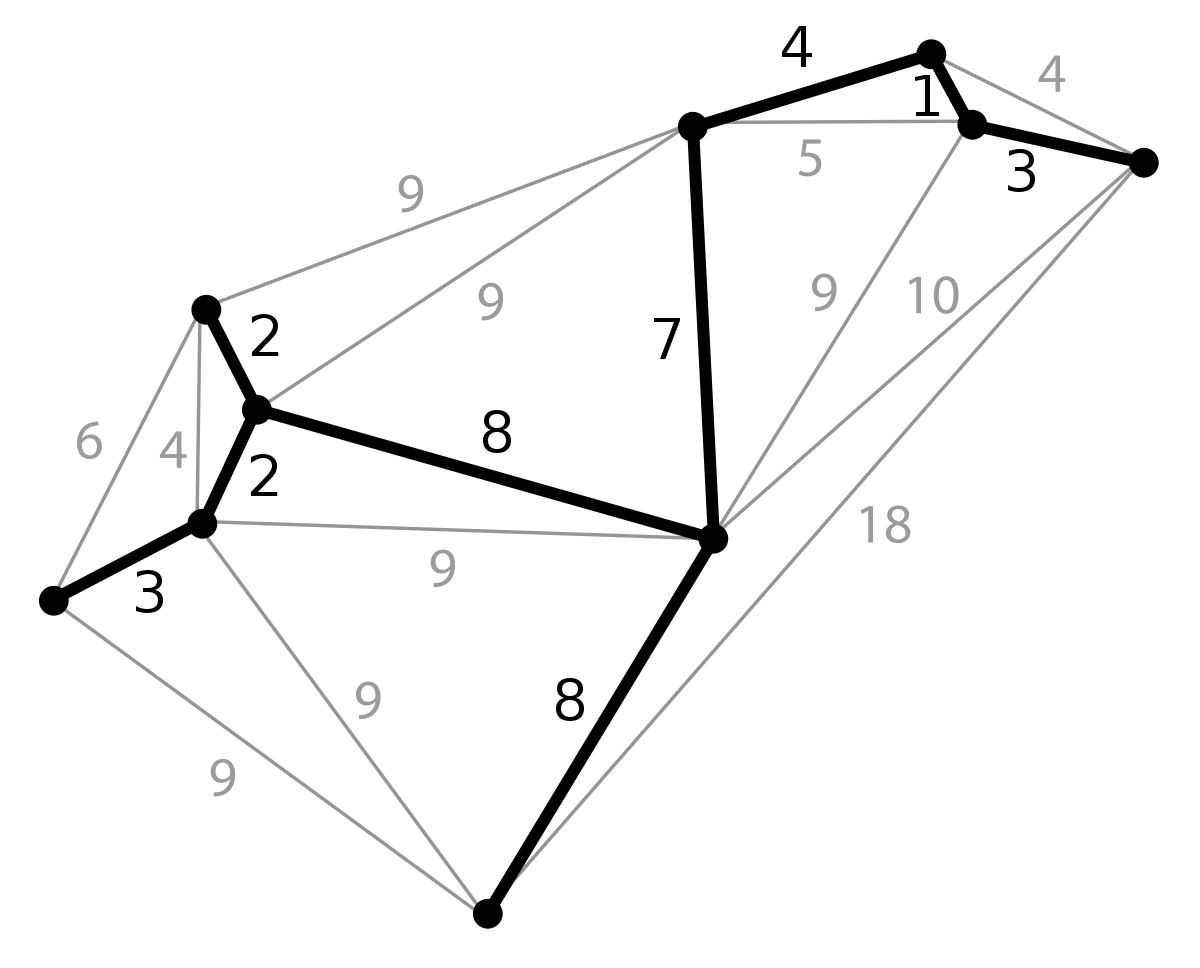网络是边有权重的无向连通图，最小生成树(MST)通常指无负权边的网络中，总边权和最小的生成树。MST有许多实际应用，如“已知任意城市间的距离，用总距离最短的公路连通所有城市”、“用最少长度的导线短接电路板的若干个点”。求MST的一般算法是Kruskal算法与Prim算法，其都为典型的贪心算法。给出几个较直观的引理：
1）包含网络全部顶点的无环连通图是该图的生成树
2）生成树的边数是顶点数-1。
3）生成树添加任意一条边后必然形成环。
4）若一个网络仅包含一个环，删除环上任意一边可得该网络的生成树。
Kruskal算法（并查集优化）
算法逻辑流程如下：
1）初始化含网络G所有顶点，但无边的子图G’，此时顶点就是连通分量。
2）从G中找权值最小（先把边权排序记录），且可连接G’某两个连通分量的边，将该边取出加入G’。
3）循环上述2步骤，直到G’只含一个连通分量时，算法结束。
算法逻辑流程的正确性证明如下：
1）首先对于上述Kruskal算法流程，得到的显然是生成树，需要证明的是该生成树是否是最小生成树。
2）把求出的生成树计作T，取图的一个最小生成树M。假设T!=M，则T必含一条以上的边不属于M，取Kruskal算法执行时加入T的第一条不属于M的边计作e。
3）若把e加入M，则必在M形成环，且可在环中找到一个不属于T的边f（因为形成了环）。然后研究e与f的权重关系。
4）若weight(e)>weight(f)，说明f在算法某一步被跳过，此时加入f不能连通两个连通分量（等于会形成环）。e是算法加入T的第一条不属于M的边，所以在e边加入前T和M相同，由于f在M中，但M没有形成环，所以导致矛盾。
5）若weight(f)>weight(e)，此时删去环中的f，可以得到比M更小的生成树，与M是最小生成树矛盾。
6）故weight(f)=weight(e)，此时删去环中的f，可得最小生成树M’，这是用T的第一条不属于M的边替换M的一条边得到的最小生成树，重复该步骤可用T所有不属于M的边替换M的边，最终得到的也是最小生成树，说明T是最小生成树。
利用并查集实现该算法时，其实际流程如下：
1）初始化并查集，其中每个图顶点被初始化为每个单元素动态集；
2）把图边递增排序为序列；
3）从左到右遍历图边序列，若当前边两顶点属于不同动态集，合并两动态集，并把该边标记为MST边；
用并查集是因为对“如何判断边是否连接当前\(G’\)的两个连通分量”等操作有不同代价的实现，由于并查集每种运算的代价接近\(O(1)\)，故算法代价为边排序\(O(|E|lg|E|)\)。任何无向图满足\(|E| \leq |V|^2\)，故代价可计为\(O(|E|lg|V|)\)。由于连通图的边集含全部顶点，故直接用“边列表”表示图与求得的最小生成树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 | #!python3.7 class DynamicNode: def __init__(self, key): self.key = key self.rank = 0 self.p = self class DisjointSet: def make(self, key): return DynamicNode(key) def find(self, x): if x.p != x: x.p = self.find(x.p) return x.p def _link(self, x, y): if x.rank > y.rank: y.p = x else: x.p = y if x.rank == y.rank: y.rank += 1 def union(self, x, y): self._link(self.find(x), self.find(y)) def kruskal(graph): ds = DisjointSet() mapper = {} for e in graph: if not mapper.get(e[0]): mapper[e[0]] = ds.make(e[0]) if not mapper.get(e[1]): mapper[e[1]] = ds.make(e[1]) graph.sort(key=lambda x: x[2]) mst = [] for e in graph: n1, n2 = mapper[e[0]], mapper[e[1]] if ds.find(n1) != ds.find(n2): mst.append(e) ds.union(n1, n2) return mst graph = [ ('a', 'b', 4), ('c', 'b', 3), ('e', 'a', 3), ('a', 'c', 5), ('b', 'e', 4), ('e', 'd', 2), ('b', 'd', 3), ] print(kruskal(graph)) |
Prim算法（堆优化）
算法逻辑流程如下：
1）初始化含网络G任意一个顶点，但无边的子图G’。
2）从G中找权值最小（先把边权排序记录），且一端顶点在G’另一端不在G’的边。将该边/顶点取出加入G’（若此时有多组满足条件的边/顶点，任取一组即可）
3）循环上述2步骤，直到G’与G顶点集相同，算法结束。
算法逻辑流程的正确性证明如下：
1）首先对于上述Prim算法流程，得到的显然是生成树，需要证明的是该生成树是否是最小生成树。
2）把求出的生成树先计作T，取图的一个最小生成树M。假设T!=M，则T必含一条以上的边不属于M，任取一条边e。
3）若把e加入M，则必在M形成环，且可在环中找到一个不属于T的边f（因为形成了环）。然后研究e与f的权重关系。
4）若weight(f)<weight(e)，由于e/f分别不属于M/T，根据引理(4)若此时对T加入f删去e，可以得到另外一个权重小于T的生成树，说明Prim算法在某次加边时，有权值更小的边可选，这导致与算法步骤矛盾。
5）若weight(f)>weight(e)，此时删去环中的f，根据引理(4)可以得到比M更小的生成树，与M是最小生成树矛盾。
6）故weight(f)=weight(e)，此时删去环中的f，可得最小生成树M’，这是用T的一条边替换M的一条边得到的最小生成树，由于e边的选择是任意的，重复该步骤可以把M中所有与T不同的边替换掉，最终说明T是最小生成树。
利用小根堆(二叉堆)实现该算法时，其实际流程如下：
1）把所有顶点按索引为\(\infty\)建成\(H\)小根堆(二叉堆)；
2）从\(H\)任选顶点将其索引\(decrease\)为0，准备作为图\(G’\)中的所谓初始顶点；
3）从\(H\)中出堆顶点\(u\)并遍历其邻接顶点\(v\)，若\(u\)的索引大于边权\(w(u,v)\)，则将其索引\(decrease\)为\(w(u,v)\)，循环该步骤直到\(H\)为空。对于第1次循环是出堆图\(G’\)的初始顶点，从第2次循环开始，每次出堆的顶点是“可到达目前已出堆顶点的最小权重邻接顶点”，注意到如果记录顶点“最后1次索引\(decrease\)”时对应的边，那么这个边的意义即“可到达目前已出堆顶点的最小权重边”，若每次出堆时也可以得到这个边，那么出堆所得到的全部边就构成一个MST；
采用二叉堆是逻辑流程(2)有不同实现，用二叉堆的\(decrease\)可方便的把“已出堆顶点的最小权重未出堆邻接顶点”放在优先队列头部，每次\(decrease\)的代价上界为\(lgV\)。总代价\(O( (E+V)lgV ) = O( ElgV )\)，若进一步利用斐波那契堆代替二叉堆，则代价为\(O(E+VlgV)\)。
但要注意Prim算法使用的二叉堆和之前文章中的二叉堆实现不太一样，需要自己建立好相关的映射关系，所以这里定义了一个叫做PrimHeap的魔改版的二叉堆来辅助算法的实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 | class PrimHeap: @staticmethod def parent(idx): if idx <= 0: return 0 if idx % 2 == 0: return idx // 2 - 1 if idx % 2 == 1: return idx // 2 @staticmethod def left(idx): return 2 * idx + 1 @staticmethod def right(idx): return 2 * idx + 2 def __init__(self): self.arr = [] self.indexs = {} self.values = set() def is_empty(self): return len(self.arr) == 0 def _build(self, idx, last_idx): l = self.left(idx) r = self.right(idx) x = idx x = l if l <= last_idx and self.arr[l][0] < self.arr[idx][0] else x x = r if r <= last_idx and self.arr[r][0] < self.arr[x][0] else x if x != idx: self.arr[x], self.arr[idx] = self.arr[idx], self.arr[x] self.indexs[self.arr[x][1]] = x self.indexs[self.arr[idx][1]] = idx self._build(x, last_idx) def get(self): if len(self.arr) == 0: return None if len(self.arr) == 1: value = self.arr.pop()[1] self.indexs.pop(value) self.values.remove(value) return value self.arr[-1], self.arr[0] = self.arr[0], self.arr[-1] self.indexs[self.arr[0][1]] = 0 self.indexs[self.arr[len(self.arr)-1][1]] = len(self.arr)-1 self._build(0, len(self.arr)-2) value = self.arr.pop()[1] self.indexs.pop(value) self.values.remove(value) return value def decrease_by_index(self, index, priority): self.arr[index] = (priority, self.arr[index][1]) p = self.parent(index) while index > 0 and self.arr[p][0] > self.arr[index][0]: self.arr[index], self.arr[p] = self.arr[p], self.arr[index] self.indexs[self.arr[index][1]] = index self.indexs[self.arr[p][1]] = p index = p p = self.parent(index) def put(self, priority, value): assert value not in self.values, '该value已在堆中' index = len(self.arr) self.values.add(value) self.arr.append((float('inf'), value)) self.indexs[value] = len(self.arr) - 1 self.decrease_by_index(index, priority) def decrease_by_value(self, value, priority): index = self.indexs[value] self.decrease_by_index(index, priority) def get_value_priorty(self, value): index = self.indexs[value] return self.arr[index][0] def has_value(self, value): return value in self.values def prim(graph): bound = max([i[2] for i in graph] if graph else [0]) + 1 adj = {} for e in graph: if e[0] not in adj: adj[e[0]] = {} if e[1] not in adj: adj[e[1]] = {} adj[e[0]][e[1]] = e adj[e[1]][e[0]] = e nodes = [k for k in adj.keys()] ph = PrimHeap() for k in range(len(nodes)): if k == 0: ph.put(0, nodes[k]) else: ph.put(bound, nodes[k]) min_edge = {} while not ph.is_empty(): u = ph.get() for v in adj[u]: e = adj[u][v] w = e[2] if ph.has_value(v): priority = ph.get_value_priorty(v) if w < priority: min_edge[v] = e ph.decrease_by_value(v, w) mst = list(min_edge.values()) return mst graph = [ ('a', 'b', 2), ('c', 'b', 2), ('d', 'a', 6), ('a', 'c', 3), ('b', 'd', 3) ] print(prim(graph)) |