无符号整数的机器级表示
计算机是通过二进制位存储和传输数据的。虽然这些二进制位适合表示二进制数,但还是有一定区别,比如寄存器和总线的位数通常是固定的,另外对于负号、小数点、分数等等都不能直接表示,需要规定一些规则计算机才能处理。这些规则中,最简单的就是对无符号整数的表示,无符号整数顾名思义就是没有符号的整数,也就是自然数。这种表示和数学上的表示几乎没有区别,只需要预先规定好占用的位数,并且需要高位补0,比如在4位无符号整数表示下,3要写作0011,而3对应的二进制数是11。 一般的k位无符号整数,能表示的十进制数范围是闭区间的\([0,2^k–1]\)。
无符号整数的加法
之前讨论行波进位加法器时,没有规定如何处理最低位进位输入、最高位进位输出,这里规定为“忽略最高位进位的输出,最低位进位输入始终保持0”。当两个\(k\)位无符号整数码输入到\(k\)位加法器(\(k\)个1位加法器组成的行波进位加法器),若结果未超出\(k\)位,那么加法器的输出就是正确的和。但若超出\(k\)位(两个\(k\)位无符号整数码经过加法器最多只能超出1位),则加法器会忽略掉最高位的进位,剩下的\(k\)位才是最终输出,这种情况称为加法器的溢出,可通过余数描述。在这种规定下,这种\(k\)位加法器就能做\(k\)位无符号整数码的加法,具体这样描述:
a) 若\(a,b\)在\(k\)位无符号整数码的表示范围,将\(a,b\)的\(k\)位无符号整码通过该\(k\)位加法器,把结果看作\(k\)位无符号整码,其表示的值是\((a+b) ~ mod ~ 2^k\);
之后讨论的其他\(k\)位码的算术运算,加法器默认都指同样位数的\(k\)位加法器。
无符号整数的“按位取反+1”
“按位取反+1”分两步,第一步是逻辑运算的按位取反,第二步是把按位取反的结果按上述加法做+1。“按位取反+1”这种奇怪运算对于计算机很重要,计算机借助该运算能够用“加法”实现“减法”,之后要讨论的补码也与该运算有关。实现按位取反的硬件十分简单,无需讨论其电路,只讨论“按位取反+1”输入的码和输出的码所表示的值的关系。这里直接给出结论:
b) 若\(a\)在\(k\)位无符号整数码的表示范围内,把\(a\)的\(k\)位无符号整码做‘按位取反+1’后的结果看作\(k\)位无符号整码,其表示的值是\((- a) ~mod~ 2^k\);
所以“按位取反+1”是用于处理“负”和“减法”的一种操作,虽然无符号整数码不能表示负数,但是在余数式中能加上负号。上述结论的正确性容易验证,\(a=0\)时溢出后也等于0。\(a>0\)时,将按位取反+1的结果所表示的值计为\(x\),由于\(a,x\)的码做加法会溢出且全部位都剩下0,所以\(a+x = 2^k\),\(x = 2^k – a = (2^k – a) ~mod~ 2^k = (- a) ~mod~ 2^k \)。
无符号整数的减法
减法运算能直接通过一次上述的加法运算、一次上述的“按位取反+1”完成。具体表述如下:
c) 设\(a,b\)都在\(k\)位无符号整数码的取值范围内,将\(a\)的\(k\)位无符号整数码与\(b\)的\(k\)位无符号整数码的“按位取反+1”做上述加法,把结果看作\(k\)位无符号整数码,其表示\((a-b) ~mod~ 2^k\);
容易验证该结论,加法器输出看作\(k\)位无符号整数码表示\((a + ((- b) ~mod~ 2^k)) ~mod~ 2^k\)。考虑\(a \in [0,2^k – 1]\),其可写成\(((a ~mod~ 2^k) + ((- b) ~mod~ 2^k)) ~mod~ 2^k\)。用余数加法定理可写成\((a-b) ~mod~ 2^k\)。然后分情况讨论:
1) \(a-b\)在\(k\)位无符号整数码取值范围:则\((a-b) ~mod~ 2^k = a-b\)。说明这种“减法”是正确的;
2) \(a-b\)不在\(k\)位无符号整数码取值范围:这时\(-(2^k-1) \leq a-b<0\),故\((a-b) ~mod~ 2^k = 2^k+a-b\)。是\(a-b\)不在取值范围内时导致的错误结果。但这个错误结果一定程度上可以“补救”。比如设\(a,b,c,a-b+c\)都在\(k\)位无符号整数码取值范围内,但\(a-b\)是不在取值范围内的。然后假设要计算\(a-b+c\),会先按上述减法计算\(a-b\),再按上述加法计算\(+c\)。可以发现虽然做\(a-b\)会得到错误结果,但之后做\(+c\)后却能得到正确的\(a-b+c\)的结果!这一点也很容易验证,因为做完\(+c\)后加法器的输出表示的是\((2^k+a-b+c) ~mod~ 2^k\),由于\(a-b+c\)在取值范围内,所以其等于\(a-b+c\);
根据上述(2),特殊的若\(a,b\)在\(k\)位码表示范围内,\(a,b\)的码做完上述减法,再把结果用上述加法加\(b\),得到的码表示\(a\)。在之后要讨论的除法的恢复余数法中,这个结论可以保证恢复余数步骤的正确性。
另外还可以发现,只有被减数加上“按位取反+1”后的结果时发生了溢出,才说明\(a-b\)在取值范围内(才得到的是正确的减法结果),否则如果没有溢出,反而说明得到的不是正确的结果(不够减导致)。
无符号整数的逻辑移位
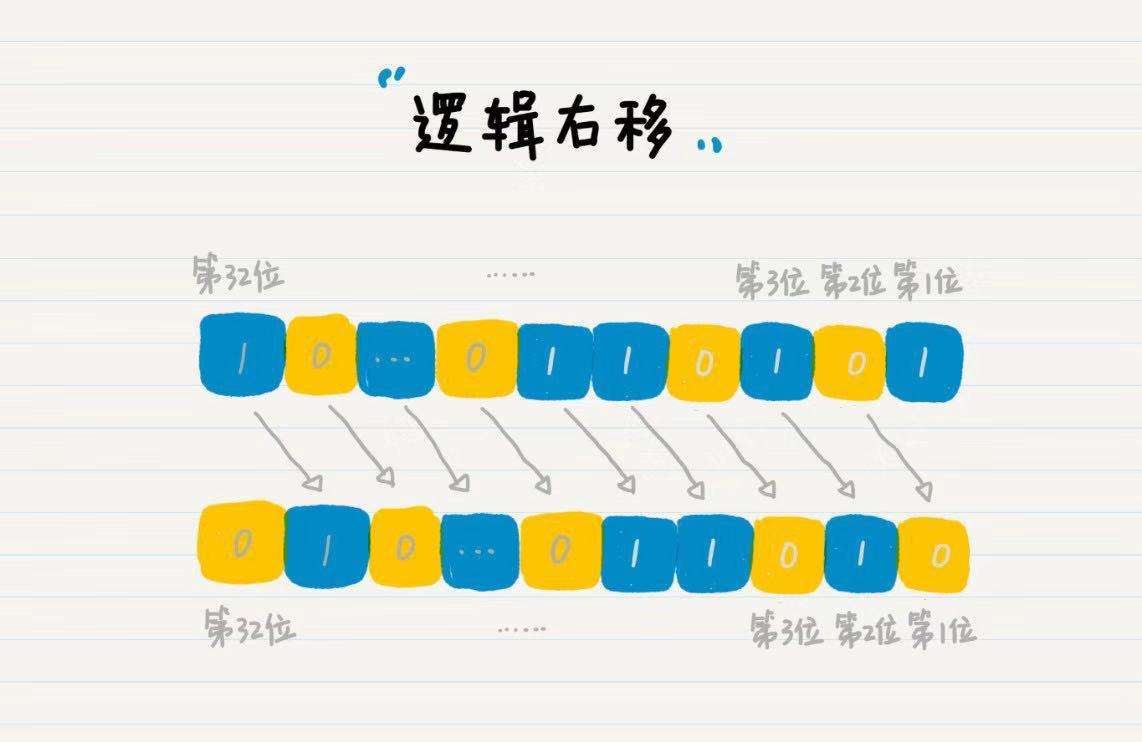
移位是二进制位中常用的逻辑运算,分为逻辑移位和算术移位。逻辑移位将被用于无符号整数乘法的实现,其规则如上,右移1位是把最低位舍弃,最高位补0,左移1位则是把最高位舍弃,最低位补0。实现移位的电路相对简单,前面讨论组合逻辑电路时,讨论过移位器。所以这里不讨论其电路。逻辑左移与无符号整数码存在这样的关系:
d) 设\(a\)在\(k\)位无符号整数码取值范围内,\(a\)的\(k\)位无符号整数码逻辑左移\(n\)次得到的\(k\)位无符号整数码表示\((a\cdot 2^n) ~mod~ 2^k\);
换句话说,每逻辑左移1位相当于乘以一次2。
无符号整数的乘法


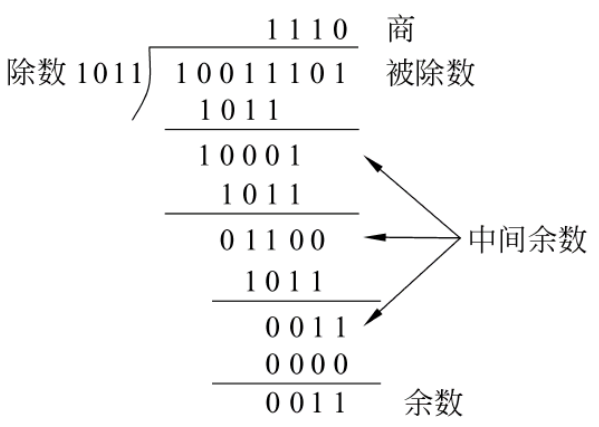
最基本的乘除法的实现方法是模拟“竖式笔算”,这类实现在国外被称为笔纸算法(Paper-Pencil Algorithm)。乘法竖式的思路是用乘数的每个位去乘以被乘数得到多个“部分积”,然后把所有部分积相加得到积。
上图是二进制数的乘法竖式,左边是没有补齐高位的,右边是补齐高位的。二进制竖式相比其他进制的竖式有个特点,就是每个“部分积”不是0就是被乘数的逻辑左移。所以\(k\)位无符号整数码的乘法可通过让多个逻辑左移后的被乘数的\(k\)位无符号整数码相加实现,这就是乘法的移位相加法。然后看这种方法的具体流程,为方便描述,假设有A,B,C这2个\(k\)位寄存器:
1) A存被乘数的\(k\)位无符号整数码,B存乘数的\(k\)位无符号整数码,C填0;
2) 循环\(k\)次如下的步骤:
2.1) 若当前B最低位是1,用加法器做C=A+C。否则跳过该步骤;
2.2) A逻辑左移1位、B逻辑右移1位;
3) 循环结束后C就是积的\(k\)位无符号整数码;
这里简单的把这种乘法叫保留\(k\)位积乘法。其正确性借助余数性质比较容易证明,最后的结论是这样:
e) 设\(a,b\)都在\(k\)位无符号整数码的取值范围内,将\(a,b\)的\(k\)位无符号整数码做上述保留\(k\)位积的乘法,把结果看作\(k\)位无符号整数码,其表示\(ab ~mod~ 2^k\);
对于这种被乘数、乘数、积都是\(k\)位无符号整数码的乘法,其会浪费寄存器的位,因为被乘数和乘数如果太大会导致错误的积,所以被乘数和乘数的高位都必须是0。所以实际计算机更多使用被乘数和乘数是\(k\)位,积\(2k\)是位的乘法。这里简单的把这种乘法叫保留\(2k\)位积的乘法,其需要的寄存器是\(2k\)位的A、C和\(k\)位的B,且加法器也是\(2k\)位的,具体流程如下:
1) A低\(k\)位存被乘数的\(k\)位无符号整数码,B存乘数的\(k\)位无符号整数码,A高\(k\)位和C填0;
2) 循环\(k\)次如下的步骤:
2.1) 若当前B最低位是1,用加法器做C=A+C。否则跳过该步骤;
2.2) A逻辑左移1位、B逻辑右移1位;
3) 循环结束后C就是积的\(2k\)位无符号整数码;
由于2个\(k\)位无符号整数码所表示的数的积一定在\(2k\)位无符号整数码的取值范围内,最后的结论是这样:
f) 设\(a,b\)都在\(k\)位无符号整数码的取值范围内,将\(a,b\)的\(k\)位无符号整数码做上述保留\(2k\)位积的乘法,把结果看作\(2k\)位无符号整数码,其表示\(ab\);
ARM指令集支持这2种乘法,但最常用的是保留\(2k\)位积的乘法,原因有的上面提到了,有的之后的文章会提到。
无符号整数的除法
计算机中的整数除法一般需要能求出商和余数,除法的移位相减法是最简单的笔纸算法,其类似于移位相加乘法的逆过程。这里讨论\(2k\)位被除数和\(k\)位除数的移位相减流程,其需要使用的寄存器是\(2k\)位的A、\(k\)位的B和C。具体如下:
1) A存被除数、B存除数、C置0;
2) 循环\(k\)次如下步骤:
2.1) 将A整体逻辑左移1次;
2.2) 若A高\(k\)位不小于B,做(A高\(k\)位)=(A高\(k\)位)-B,再把A低\(k\)位的最低位设为1。否则什么也不做;
3) 循环结束后,A的高\(k\)位为余数,低\(k\)位为商;
该方法用一个\(2k\)位寄存器同时维护商和余数,模拟了二进制除法竖式。注意步骤(2.2)中要比较A高\(k\)位和B的大小,实际硬件一般不增设数值比较器电路,而是用加法器比大小。比如可“试探性”的做(A高\(k\)位)-B,若“不够减”则按前面讨论的减法步骤可判断,加法器会溢出,根据加法器溢出位即可判断大小。但这种方法还有优化的空间,因为步骤(2.2)第一步的数值比较会占用一次加法器,第二步的“(A高\(k\)位)=(A高\(k\)位)-B”又占用一次加法器,做了2次重复的减法。所以需要进一步调整,这样就能得到恢复余数法,其区别在于把步骤(2.2)替换为如下步骤:
(2.2*) 先做(A高\(k\)位)=(A高\(k\)位)-B。若加法器未溢出,说明A高\(k\)位不小于B,把A低\(k\)位的最低位设为1。若加法器溢出,说明“不够减”,需恢复A高\(k\)位为执行减法前的值(恢复余数),这只需再做一次加法(A高\(k\)位)=(A高\(k\)位)+B即可;
注意(2.2*)中加法器溢出后,再做一次加法能正确恢复原本的A高\(k\)位。这一步的正确性实际上在前面无符号整数减法中讨论过。可这样描述该加法器下的移位相减除法:
g) 设\(a,b\neq 0\)在\(k\)位码表示范围内,\(a,b\)的码在经上述移位相减后,得到的2个码分别表示的值是\(a\div b\)与\(a~mod~b\);