数据结构的持久化

可持久化数据结构

可持久化数据结构上的运算在修改自身时(比如插入、删除这样的运算)，会先记录一个改变前的状态作为历史版本，这个历史版本往往是可继续查阅和修改的。可持久化数据结构按“持久化程度”可分2大类：

1) 部分持久化数据结构：所有历史版本都可供查询，但只能基于最新版本修改数据；

2) 完全可持久化数据结构：所有历史版本都可查询修改；

通常来说设计可持久化数据结构的主要思想是“拷贝部分原有内容+复用部分原有内容”。所以可持久化数据结构的空间复杂度会介于“非可持久化数据结构”和“每次修改前完整克隆当前版本”这两种情况之间。下面就来讨论如何基于Treap构建可持久化的平衡树，这里需要引入一个称为无旋Treap的数据结构，因为“可持久化+旋转”比较难一起处理。

无旋Treap

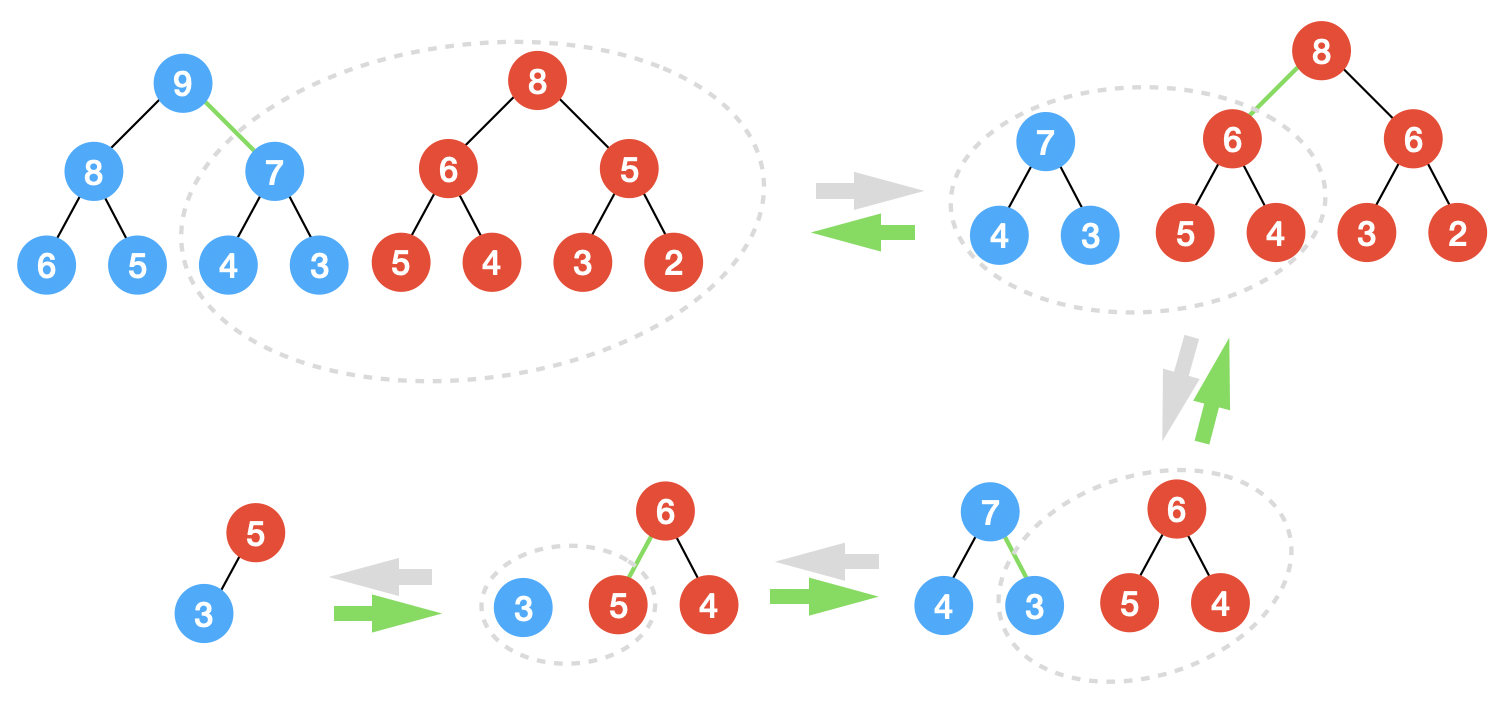 (a)

  (b)

该数据结构是清华姚班、旷视科技的范浩强中学时提出的。其没有旋转但定义了“合并”与“分裂”的运算：

1) \(merge(a,b)\)：将\(a,b\)为根的2个Treap合并并返回新根。其中\(a\)树任意节点的BST索引不大于\(b\)树；

2) \(split(a,val)\)：把\(a\)为根的Treap分裂为\(l,r\)为根的2个Treap并返回\((l,r)\)。其中\(l\)树任意节点的BST索引小于等于\(val\)，\(r\)树任意节点的BST索引严格大于\(val\)(这个边界区分很重要)；

基于“合并”与“分裂”的无旋Treap运算，很容易就可实现平衡树的运算：

1) \(find(x,y)\)：等于BST的查询运算；

2) \(insert(x)\)：把根节点分裂为\(l,r\)，合并\(l,x\)为新树，合并新树和\(r\)作为新树根；

3) \(remove(x)\)：把根节点2次\(split\)为3个子树，其BST索引为“小于等于\(x-1\)、等于\(x\)、大于\(x\)”。然后把“等于\(x\)”的子树的左右子树合并(即删树根)得到新树。把新树和其他两个子树合并得到新树根；

然后考虑如何实现上述的“合并与分裂”两个基础运算：

1) \(merge(a,b)\)：\(merge\)的前提条件是\(a\)树任意节点的BST索引不大于\(b\)树，且\(a,b\)都满足堆性质。合并的递归过程如上图(a)所示，如果\(a\)的大根堆索引大于\(b\)，那么就可以递归的\(merge(a.right,b)\)并把结果作为新\(a.right\)。反之则需要递归的\(merge(a,b.right)\)。这样才能同时维护堆性质和BST性质。

2) \(split(a,val)\)：\(split\)的结果如上图(b)。若\(val\)小于\(a\)的BST索引，递归\(split(a.left,val)\)为\(l,r\)的两个树，那么“\(l\)子树”和“\(r\)、\(a\)、\(a.right\)构成的子树”是\(a\)的\(split\)结果。反之递归\(split(a.right,val)\)为\(l,r\)左右两个子树，“\(a.left\)、\(a\)、\(l\)构成的子树”和“\(r\)子树”是\(a\)的\(split\)结果。

可以发现\(merge\)能够比较随机的把两个BST随机的拼接在一起，并且不违反BST性质。这种拼接方式能够调整BST各子树的高度，如果拼接是随机的，那么就可以实现和普通Treap相似的恢复平衡的功能。并且由于\(merge\)和\(split\)的递归过程是按树高度推进的，所以每次运算的平均代价是\(O(lgN)\)。

无旋Treap的持久化

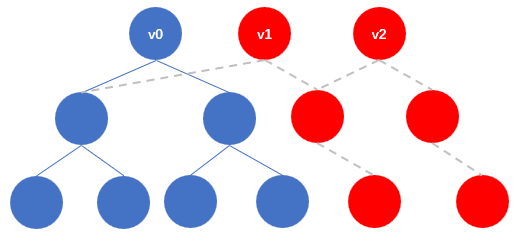
在“无父指针二叉树”这种物理结构下做持久化时，往往会利用“孩子不记录父亲”的性质，允许节点在不同版本中有不同的父亲，这样就能通过复用节点来减少拷贝，降低时间与空间复杂度。上图是一个持久化二叉树的例子，蓝色节点代表初始时v0版本的树，红色节点代表之后创建的节点。可以看到v0,v1,v2共用了一部分节点，并且也不会导致矛盾。下面通过改造合并与分裂两个基本运算实现可持久化：

1) \(merge(a,b)\)：原\(merge\)的第一步是递归的执行\(merge(a.right,b)\)或\(merge(a,b.left)\)，第二步是把返回的树根设为\(a.right\)或\(b.left\)，第三步返回\(a\)或\(b\)。这里从第二步开始修改，首先克隆节点\(a\)为\(a’\)或\(b\)为\(b’\)，然后设定\(a’.left=a.left\)或\(b’.right=b.right\)，再把原第一步所返回的节点设置为\(a’.right\)或\(b’.left\)，最后返回\(a’\)或\(b’\)。这样定义的新\(merge(a,b)\)运算就不会改变原\(a,b\)两个子树，且由于\(merge\)递归是按树高推进的，故\(a,b\)接近满二叉树时，克隆节点数有上界\(a,b\)高度和的对数。

2) \(split(a,val)\)：具体实现的思路和上述\(merge\)十分相似，也是通过创建新根来取代切断树边的操作，这样就不会改变原\(a\)树，具体操作对比上下两版代码的差异即可，这里不展开讨论。如果\(a\)的形态接近满二叉树，同样其额外创建的节点数有上界等于\(a\)高度的对数。