SPLAY树

SPLAY树(伸展树)

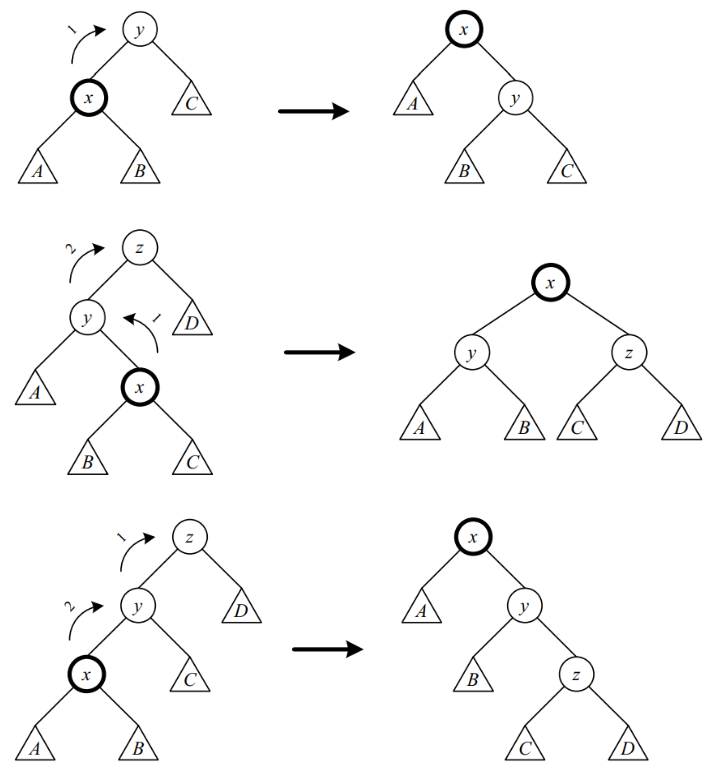
1985年美国学者Daniel Sleator和Robert Tarjan提出Splay树，其能保证运算的摊还代价是\(O(\lg{n})\)，但不保证每次运算的实际代价都是\(O(\lg{n})\)，所以其并非严格意义上的自平衡二叉树，但这也使其有更简单的定义和运算步骤。这里直接给出Splay树的定义，首先其运算功能和前文的BST一致，且运算开始前只需保证二叉树是BST，但运算步骤是被具体规定的，它们都必须基于伸展运算\(splay(x)\)，其功能是通过多次单旋转使\(x\)成为树根。下面给出Splay树运算的步骤，其包括\(splay(x)\)的步骤：

1) \(splay(x)\)：开始迭代过程，每轮迭代的步骤如下：

1.1) \(x\)无父亲：退出迭代；

1.2) \(x\)有父亲无祖父：对\(x\)的父亲执行1次单旋转使\(x\)取代其父亲的位置(见上图第1张)。退出迭代；

1.3) \(x\)有祖父且\(x\)的父亲和祖父分别是左右节点或分别是右左节点：对\(x\)的父亲执行1次单旋转使\(x\)取代其父亲的位置。然后再对\(x\)此时的父亲执行1次单旋转使\(x\)取代其此时的父亲的位置(见上图第2张)。继续迭代；

1.4) \(x\)有祖父且\(x\)的父亲和祖父都是左节点或都是右节点：对\(x\)的祖父执行1次单旋转使\(x\)的父亲取代其祖父的位置。然后再对\(x\)此时的父亲执行1次单旋转使\(x\)取代其此时的父亲的位置(见上图第3张)。继续迭代；

2) \(insert(k)\)：先执行BST的\(insert(k)\)得到新节点\(x\)(按之前讨论BST的文章中的步骤)。然后执行\(splay(x)\)；

3) \(find(k)\)：可根据BST的\(find\)改造得到(按之前讨论BST的文章中的步骤)。具体是在每轮迭代刚开始时就额外用\(x’\)记录当前节点，那么整个迭代结束时，无论是否查找成功，\(x’\)总表示整个迭代过程所访问到的最深节点，之后称其为\(find\)的最后访问节点。最后如果\(x’\)非空(显然仅当二叉树为空树时其为空)还必须额外执行\(splay(x’)\)；

4) \(remove(k)\)：先执行上述\(find(k)\)。若查找失败则退出，否则将查找成功得到的节点计为\(x\)。若\(x\)无孩子则置空树根。若\(x\)只有1个孩子则置树根为该孩子(并将该孩子的\(parent\)置空)。若\(x\)有2个孩子则初始化\(l,r\)分别指向\(x\)的左右孩子，置树根为\(l\)(并将\(l\)的\(parent\)置空)，找到\(l\)子树的最右节点\(l’\)，执行\(splay(l’)\)，最后置\(l’.right=r\)(并将\(r\)的\(parent\)指向\(l’\))；

至此已完成对Splay树的定义，需注意到Splay树完全不限制BST的形态，任何BST都能作为Splay树来执行上述运算，并且随着运算次数增加，二叉树的高度会逐步的“收敛”至\(O(\lg{n})\)。可以发现这种能让任何BST都逐步“恢复平衡”的性质十分特殊，大部分的传统自平衡树(红黑树、AVL树等)不仅不具备该特性，并且如果执行运算前不符合相应的形态等各方面的限制，还会产生各种难以预料的错误。总之Splay树的这个特性很重要，之后在分析Splay树的时间复杂度时会证明该特性。

SPLAY树的时间复杂度

首先给出之后会用到的辅助公式如下：

a1) 设\(a>0,b>0,c\geq a+b\)，则\(\log_2{a}+\log_2{b}-2\log_2{c}\leq -2\)；

证明：由于\(\log_2{x}\)的二阶导数恒小于0，所以其恒为上凸函数，根据上凸函数的定义有\(\log_2{a} + \log_2{b} \leq 2\log_2{(\frac{a+b}{2})}\)。于是有不等式\(\log_2{a}+\log_2{b}-2\log_2{c} \leq \log_2{a}+\log_2{b}-2\log_2{(a+b)} \leq 2\log_2{(\frac{a+b}{2})}-2\log_2{(a+b)}=-2\)。

定义\(s(x)\)为节点\(x\)与其所有后代节点的总数，\(r(x)=\log_2{s(x)}\)。进而可定义\(\Phi(T)=\sum_{x\in T}r(x)\)，其中自变量\(T\)可以是任意的二叉树，求和符号\(\sum_{x\in T}\)表示对\(T\)的所有节点求和。显然\(\Phi(T)\geq 0\)，并且仅当\(T\)的总节点数小于2时等号成立。接下来用势能法做摊还分析，其中的势能函数为\(\Phi\)。分析过程通过命题和对命题的证明来给出：

b1) 在节点数为\(n\geq 1\)的BST执行\(splay(x)\)。执行前后\(\Delta\Phi \leq 3\log_2{(n)}-H_x+1\)，\(H_x\)是执行前\(x\)的高度；

证明：先分析某一轮迭代的势能变化\(\Delta\Phi’\)，为方便用\(s,s’\)和\(r,r’\)分别表示该轮迭代前后的\(s\)和\(r\)，然后分情况讨论：

1) 步骤(1.1)：完全无影响，\(\Delta\Phi’=0\)；

2) 步骤(1.2)：以右旋转为例(见上图1)，左旋转同理。设\(y\)是该轮迭代开始时\(x\)的父亲，该轮迭代前后仅\(x,y\)的后代数目改变，并且\(r'(x)=r(y)\)。故\(\Delta\Phi’=r'(y)+r'(x)-r(y)-r(x)=r'(y)-r(x)\leq (r'(x)-1)-r(x)\)；

3) 步骤(1.3)：以左右旋转为例(见上图2)，右左旋转同理。设\(y,z\)是该轮迭代开始时\(x\)的父亲和祖父，则该轮迭代前后仅\(x,y,z\)的后代数目改变，并且\(r'(x)=r(z)\)。同理\(\Delta\Phi’=r'(y)+r'(z)-r(y)-r(x)<r'(y)+r'(z)-2r(x)\)，将该式最右边变形可得\(\Delta\Phi’ < 2(r'(x)-r(x))+(r'(y)+r'(z)-2r'(x))\)。注意到\(s'(x)=s'(y)+s'(z)+1>s'(y)+s'(z)\)，结合该式和前面的不等式和(a1)可得\(\Delta\Phi’ <  2(r'(x)-r(x))-2\)；

4) 步骤(1.4)：以右右旋转为例(见上图3)，左左旋转同理。设\(y,z\)是该轮迭代开始时\(x\)的父亲和祖父，则该轮迭代前后仅\(x,y,z\)的后代数目改变，并且\(r'(x)=r(z)\)。同理\(\Delta\Phi’=r'(y)+r'(z)-r(y)-r(x)<r'(y)+r'(z)-2r(x)\)，将该式额外放缩一次可得\(\Delta\Phi’ < r'(x)+r'(z)-2r(x)\)，再对最右边变形可得\(\Delta\Phi’ < 3(r'(x)-r(x))+(r(x)+r'(z)-2r'(x))\)。注意到\(s'(x)=s(x)+s'(z)+1>s(x)+s'(z)\)，结合该式和前面的不等式和(a1)可得\(\Delta\Phi’ <  3(r'(x)-r(x))-2\)；

对于(2)(3)(4)情况，综上有\(\Delta\Phi’ <  3(r'(x)-r(x))-2\)。然后分析整个迭代过程的势能变化，首先最后一轮迭代只能是情况(1)(2)，其他轮则只能是(3)(4)。设迭代总轮数为\(k\geq 1\)，并将第\(i\)轮迭代后的\(r\)计为\(r^{(i)}\)(最初的\(r\)仍计为\(r\))。若\(k=1\)且这轮迭代是情况(1)则\(H_x=1,\Delta\Phi=0\)。若\(k=1\)且这轮迭代是情况(2)则\(H_x=2,\Delta\Phi <  3(r^{(1)}(x)-r(x))-2\leq 3r^{(1)}(x)-2\)，这轮迭代结束时\(x\)成为树根，所以\(\Delta\Phi<3\log_2{(n)}-2=3\log_2{(n)}-H_x\)。若\(k>1\)且最后一轮迭代是情况(1)则\(\Delta\Phi\)由前\(k-1\)轮迭代决定，所以\(H_x=2(k-1)+1,\Delta\Phi< 3(r^{(k-1)}(x)-r(x))-2(k-1) \leq 3r^{(k-1)}(x)-2(k-1)\)，第\(k-1\)轮迭代结束时\(x\)就已经成为树根，所以\(\Delta\Phi<3\log_2{(n)}-2(k-1)=3\log_2{(n)}-H_x+1\)。若\(k>1\)且最后一轮迭代是情况(2)则\(\Delta\Phi\)由所有轮迭代决定，所以\(H_x=2(k-1)+2,\Delta\Phi< 3(r^{(k)}(x)-r(x))-2k \leq 3r^{(k)}(x)-2k\)，第\(k\)轮迭代结束时\(x\)成为树根，所以\(\Delta\Phi<3\log_2{(n)}-2k=3\log_2{(n)}-H_x\)。综合这4种情况有\(\Delta\Phi \leq 3\log_2{(n)}-H_x+1\)。

b2) 在节点数为\(n\geq 1\)的BST执行\(find\)。执行前后\(\Delta\Phi \leq 3\log_2{(n)}-H_x+1\)，\(H_x\)是执行前最后访问节点\(x\)的高度；

证明：由于\(n\geq 1\)，所以\(x\)存在且会执行\(splay(x)\)，故\(\Delta\Phi\)为\(splay(x)\)造成的势能变化，结合(b1)可得上述结论。

b3) 在节点数为\(n\geq 1\)的BST执行\(insert\)。执行前后\(\Delta\Phi \leq 4\log_2{(n+1)}-H_x+1\)，\(H_x\)是\(splay(x)\)前新节点\(x\)的高度；

证明：先分析BST插入前后的势能变化\(\Delta\Phi_1\)。在BST插入刚完成时设\(x\)有\(k\)个祖先，由于\(n\geq 1\)所以有\(k\geq 1\)，然后将这些祖先“由近到远”计为\(x_1…x_k\)。BST插入前后二叉树多了个新节点，原节点仅\(x_1…x_k\)的后代总数目有变化，并且都是+1，如果约定函数\(s\)表示BST插入前的\(s\)，则有\(\Delta\Phi_1=log_2{1}+\sum_{i=1}^k [\log_2{(s(x_i)+1)}-\log_2{(s(x_i)})]=\log_2(\prod_{i=1}^k\frac{s(x_i)+1}{s(x_i)})\)。注意到任意父子节点\(x_{i+1},x_i\)都满足\(s(x_{i+1})\geq s(x_i)+1\)，所以有\(\Delta\Phi_1 \leq \log_2{[(\prod_{i=1}^{k-1}\frac{s(x_{i+1})}{s(x_i)})\frac{s(x_k)+1}{s(x_k)}]}=\log_2(\frac{s(x_k)+1}{s(x_1)})\)。注意到\(x_k\)即BST插入前的树根，所以有\(\Delta\Phi_1 \leq \log_2(\frac{n+1}{s(x_1)}) \leq \log_2{(n+1)}\)。BST插入结束后会执行\(splay(x)\)，根据(b1)可直接得到该步骤导致的势能变化\(\Delta\Phi_2\leq 3\log_2{(n+1)}-H_x+1\)。综上有\(\Delta\Phi= \Delta\Phi_1+ \Delta\Phi_2=4\log_2{(n+1)}-H_x+1\)。

b4) 在节点数为\(n\geq 1\)的BST执行\(remove\)。若\(find\)子步骤结束后未再执行\(splay\)，则执行前后有\(\Delta\Phi \leq 3\log_2{(n)}-H_{x}+1\)。若\(find\)子步骤之后还执行了\(splay(y)\)，则有\(\Delta\Phi < 6\log_2{(n)}-H_{x}-H’_{y}+2\)。前面的\(H_x\)都是\(remove\)执行前\(find\)子步骤的最后访问节点\(x\)的高度，\(H’_y\)则是\(splay(y)\)执行前的\(y\)的高度；

证明：先将\(find\)子步骤导致的势能变化计为\(\Delta\Phi_1\)，由于\(n\geq 1\)故\(x\)非空，根据(b1)有\(\Delta\Phi_1 \leq 3\log_2{(n)}-H_x+1\)。若\(find\)子步骤结束后未再执行\(splay\)，则有\(\Delta\Phi \leq \Delta\Phi_1\)，因为删除成功的情况并不增大势能。若\(find\)子步骤结束后执行了\(splay(y)\)，则先回到\(find\)子步骤刚刚结束时，将此时的树根\(x\)的左右子树分别计为\(T_L\)与\(T_R\)，将此时\(T_L\)的总节点数计为\(n_L\)，则此时的总势能可表示为\(\Phi’=\Phi(T_L)+\log_2{n}+\Phi(T_R)\)。下一步是用\(T_L\)取代二叉树，此时总势能变为\(\Phi(T_L)\)。下一步是执行\(splay(y)\)，根据(b1)此时的总势能不超过\(\Phi(T_L)+3\log_2{(n_L)}-H’_y+1 < \Phi(T_L)+3\log_2{(n)}-H’_y+1\)。最后一步是使\(T_R\)成为当前树根的右子树，此时总势能小于\(\Phi(T_L)+3\log_2{(n)}-H’_y+1+ [(\log_2{(n-1)}-\log_2{(n_L)}) +\Phi(T_R)]\)，整理可得其减\(\Phi’\)的差小于\((\log_2{(n-1)}-\log_2{(n_L)}-\log_2{n})+3\log_2{(n)}-H’_y+1 \leq 3\log_2{(n)}-H’_y+1\)，进而可得出总势能的变化量满足\(\Delta\Phi < \Delta\Phi_1+3\log_2{(n)}-H’_y+1\)。综合前面2种情况，上述命题成立。

根据上述命题可得到关于Splay树的摊还分析结论，这里通过命题和对命题的证明给出：

c1) 在节点数为\(n>0\)的BST执行\(m\)次\(find,insert,remove\)运算，其总代价有上界\(O(m\lg{(n+m)} + n\lg{n})\)；

证明：根据\(find,insert,remove\)的步骤。若这3种运算执行前BST为空树，则其实际代价都为常数，其导致的势能变化量都是0，其中\(insert\)导致的变化量为\(\log_2{1}-0=0\)。若这3种运算执行前BST包含\(k\geq 1\)个节点，则\(find,insert\)的实际代价都是“\(c_1H_x+c_2\)”型的，\(remove\)的实际代价是“\(c_1(H_x+H’_y)+c_2\)”型的(没有执行\(splay(y)\)的话把\(H’_y\)当作0)。这表明在最开始定义势能函数时，就能找到合适的常数\(A>0\)用来将势能定义为\(A\Phi\)，这样就存在常数\(B>0\)使3种运算在势能\(A\Phi\)下的摊还代价都小于\(6A\log_2{(k)} + B\)，因为\(\Delta(A\Phi)\)中的\(-AH_x\)或\(-AH’_y\)足以将实际代价中关于\(H_x\)或\(H’_y\)的线性项抵扣到小于\(B\)。

注意到每次运算开始时的节点数都小于\(n+m\)，所以总摊还代价小于\(6Am\log_2{(n+m)} + Bm\)。首次运算开始前BST有\(n\)个节点，显然此时的势能等于0或小于\(An\log_2(n)\)， 而最后一次运算结束时的势能则至少为0，所以总摊还代价至多比总实际代价少\(An\log_2(n)\)，于是总实际代价小于\(6Am\log_2{(n+m)} + Bm + An\log_2(n) = O(m\lg{(n+m)} + n\lg{(n)})\)。

c2) 在节点数为\(n>0\)的BST执行\(m\)次\(splay\)运算，其总代价有上界\(O(m\lg{n} + n\lg{n})\)；

证明：与(c1)同理，将节点总数的上限从\(n+m\)改为\(n\)即可。

上述(c2)表明在Splay树上设计新运算时，如果能在该运算中加入额外的\(splay\)运算，并保证该运算的实际代价总能“等于”该运算中的\(splay\)的实际代价，则该运算的摊还代价就也可能等于\(O(\lg{n})\)，不过这也跟该运算对势能的影响有关。

总结与实现

Splay树的运算步骤本身比较简单，其最复杂的部分反而是上述的摊还分析，不过这里仍要强调几个细节。首先注意到\(splay(x)\)的步骤(1.3)和(1.4)并不对称，其中的单旋转并不总作用于当前\(x\)的当前父亲。对于\(find\)运算则必须在BST查找的基础上额外加入确定\(x’\)以及\(splay(x’)\)的步骤。如果在实现Splay树时未注意到这些细节，最终的程序可能并不会出错，但却无法保证运算代价与上述的分析结果一致。最后给出Splay树的程序实现如下，其他未提到的细节见程序与注释。