编辑距离模型
给出3种编辑距离模型中对“编辑”操作的定义:
1) Levenshtein距离:允许“替换1个字符、任意位置删1个字符、任意位置插1个字符”,权重都是1;
2) LCS距离(最长公共子序列距离):允许“任意位置删1个字符、任意位置插1个字符”,权重都是1;
3) Hamming距离:允许“替换1个字符”,权重都是1(两串长度不同时其Hamming距离是无穷);
所有编辑距离模型对“距离”的定义都是“将\(s_1\)通过模型允许的操作转化为\(s_2\)所耗费的权重”,那么最小编辑距离的定义就是“将\(s_1\)通过模型允许的操作转化为\(s_2\)需要的最小权重”。可以发现“最小编辑距离”是一类定量刻画字符串“相似度”的方案,其通过“编辑复杂程度”刻画“相似度”。
另外,最小编辑距离之所以称为“距离”是因为上述3个模型所定义的最小编辑距离满足数学上距离空间(度量空间)的性质。比如设\(L(s_1,s_2)\)为\(s_1\)到\(s_2\)的最小Levenshtein距离,其满足如下度量空间性质:
1) 正定性: \(L(s_1,s_1)=L(s_2,s_2)=0\)
2) 对称性: \(L(s_1,s_2)=L(s_2,s_1)\)
3) 三角不等式:\(L(s_1,s’) + L(s’,s_2) \geq L(s_1,s_2)\)
这里简单证明一下对称性,正定性与三角不等式很容易就可以证明。设\(L\)为任意可将\(s_1\)转化为\(s_2\)的编辑操作序列。将\(L\)反转,然后把其中的“删除”改为“插入”,“插入”改为“删除”,“替换”改为“反向替换”。那么新编辑操作序列可将\(s_2\)转化为\(s_1\),且保持原编辑操作序列的长度。那么如果找到一个\(s_1\)到\(s_2\)的最小长度编辑序列,一个\(s_2\)到\(s_1\)的最小长度编辑序列,其两者的长度必须相等,否则就会导致与“最小长度”矛盾。
这里顺便讨论一下\(s_1\)到\(s_2\)的最小LCS距离(计为\(D\))与\(s_1\)与\(s_2\)之间的LCS(计为\(s_L\))的联系,这个联系就是表达式\(2|s_L| + D = |s_1|+|s_2|\)。这一点通过画图可以得出,这里不做证明。
然后定义本文要研究的“通用编辑距离模型”,其可涵盖上述3种模型。其允许3种编辑操作:
删除:去掉字符串任意指定位置的1个字符,其权重为非负的\(W_{del}\);
插入:在字符串任意指定位置插入1个字符,其权重为非负的\(W_{ins}\);
替换:将字符串任意指定位置的字符替换为另一个,其权重为非负的\(W_{rep}\);
注意这个通用编辑距离模型不一定满足度量空间的对称性性质,很容易找到反例。如果不能满足对称性,描述编辑距离必须指明“编辑的方向”,比如不能用\(s1,s2\)间的编辑距离作为描述,而是\(s_1\)到\(s_2\)的编辑距离或\(s_2\)到\(s_1\)的编辑距离。
然后简单讨论这个“通用编辑距离”为何能涵盖上述3种模型:
1) Levenshtein距离:规定\(W_{del}=W_{ins}=W_{rep} = 1\);
2) LCS距离:规定\(W_{del}=W_{ins}=1\),\(W_{rep}=1+|s_1|+|s_2|\);
3) Hamming距离:规定\(W_{del}=W_{ins}=1+max\{|s_1|,|s_2|\}\),\(W_{rep}=1\)。在这个规定下求最小编辑距离时,如果得到的值大于等于\(1+max\{|s_1|,|s_2|\}\),就认为其最小Hamming距离等于无穷;
简单的证明该方案,容易找最小LCS距离的一个上界\(1+|s_1|+|s_2|\)(删光\(s_1\)再全部插入\(s_2\)),故求得的最小距离值一定小于这个上界,即一定不包含替换操作。同样的非无穷的最小Hamming距离有上界\(1+max\{|s_1|,|s_2|\}\)。
划分图
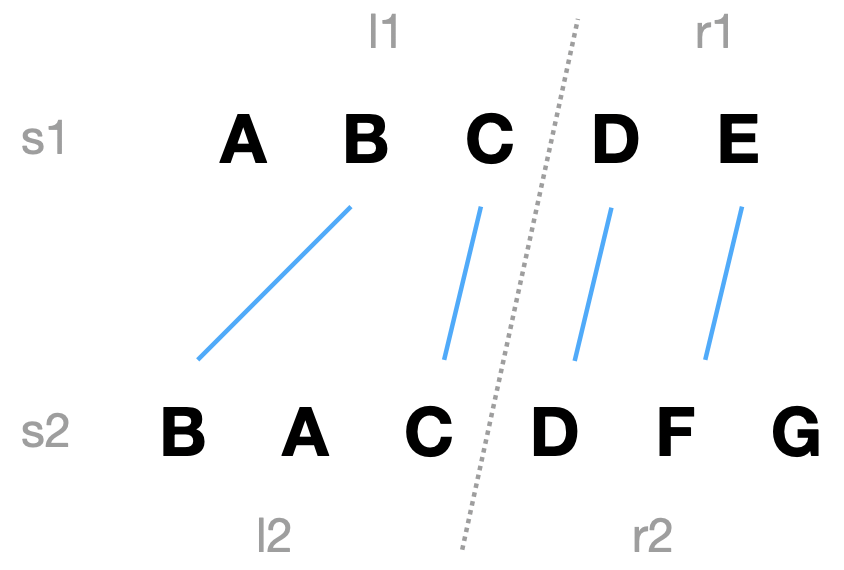
对于所有满足如下特征的编辑序列,一定能从中找到一个最小编辑距离的序列:
1) 原字符仅发生一次替换或删除操作;
2) 新字符仅发生一次插入操作;
证明:原字符如果发生了两次操作,这两次操作按顺序可以是“替换-替换”、“替换-删除”,其分别可用一次的“替换”、“删除”来代替。同样的对于新字符如果发生了连续两次操作,那么按顺序一定是“插入-替换”、“插入-删除”,其分别可替换为“插入”、“无操作”。由于约定了每个操作的权重是非负的。这些替换方式都能保证新权重不大于原权重。这里稍微提一下。如果用“替换”代替“删除-插入”则不一定满足这一点,因为这依赖于具体权重值的设定。
这样就可以只研究满足上述条件的编辑序列,不妨把满足上述条件的所有编辑序列计为\(S(s_1,s_2)\),接下来继续划分\(S(s_1,s_2)\)。定义关于\(S(s_1,s_2)\)的“1组限制信息”是对于\(s_1\)的每个字符,必须从下面3条中选1个作为限制信息:
1) 在整个编辑过程中发生1次替换,且最终“被保留”在\(s_2\)的\(j\)下标位置;
2) 在整个编辑过程中发生0次替换,且最终“被保留”在\(s_2\)的\(j\)下标位置;
3) 在整个编辑过程中被删除;
可以发现每组“限制信息”都可从\(S(s_1,s_2)\)划分1个子集,且这种“划分”满足条件:
1) 划分出的子集中的各个元素的编辑距离相等;
证明:限制条件明确了后,“原位置”的替换/删除操作即确定,而插入操作的相关信息还不能确定,但此时一定可以确定的是插入操作的总次数,因为此时插入操作的次数能够决定最终得到的字符串的位数,而最终得到的字符串的位数一定和\(s_2\)一致。
2) 划分出的子集对应的编辑距离的公式(最后一项如果小于0则最后一项的值就取0):替换次数*替换权重 + 删除次数*删除权重 + (\(s_2\)长度-(\(s_1\)长度-删除次数))*插入权重;
3) 所有合法划分所得到的子集的并集是\(S(s_1,s_2)\);
4) 任意两个合法划分所得到的子集的交集是空;
引入“划分”是为回避对“插入操作”进行具体分析,如果枚举所有“划分就可找到最小编辑距离。这里更形式化的把\(S(s_1,s_2)\)的一个“划分”计为集合\(S_d(s_1,s_2,d)\),其中\(d=[(i_1,j_1),(i_2,j_2)…]\)是对上述“1组限制条件”的表示,其中每个二元组表示上述限制(1)或限制(2),而所有二元组第一位都没覆盖到的\(s_1\)下标时,则表示删除该下标的元素,即表示限制(3)。
这里为了方便后续讨论,把“划分”用上图所示的“划分图”表示。可以直观发现“划分图”必须满足“任意2条蓝线不相交”,否则蓝线所指的\(s_1\)元素一定不能到达\(s_2\)相应的位置,在满足这一点的前提下,所有的“蓝线组合”就一一对应着所有的“划分”。
接下来引出“划分图的切割”这个概念,如上图所示的虚线,其将\(S(s_1,s_2)\)的一个“划分图”分成了两部分,这两部分刚好是\(S(l_1,l_2)\)的一个“划分图”和\(S(r_1,r_2)\)的一个“划分图”。这样的一个不与蓝线发生交叉的虚线,就可以表示一个“划分图的切割”,切割的结果就是两个“子划分图”。这里认为子划分图允许空串到空串,单字符到空串这样的边界情况。
定理a.1) 任意“划分图”对应的编辑距离,等于其“切割”给定的2个“子划分图”的编辑距离之和。
证明:直接用上面的关于“划分”的编辑距离公式即可。
定理a.2) 将任意两个“划分图”左右或右左的“拼接”,得到的“拼接图”是合法的“划分图”,且两个“划分图”的编辑距离和等于“拼接图”的编辑距离。
证明:直接用上面的关于“划分”的编辑距离公式即可。
推论b.1) 有最小编辑距离的“划分图”,其任意“切割”给定的2个“子划分图”也都对应最小编辑距离。
证明:因为这2个“子划分图”如果其中有1个有更小的编辑距离,那么根据定理(a)把这两个图“拼接”那么就能得到原问题的一个更小的编辑距离导致矛盾。
推论b.2) 拼接2个有最小编辑距离的“划分图”,得到的“拼接图”不一定对应于最小编辑距离。
证明:举个反例,’ab’编辑为’bc’的最小编辑距离是2,’cde’编辑为’dea’的最小编辑距离是2,画出对应2个满足最小编辑距离的“划分图”并“拼接”,根据公式,“拼接图”的编辑距离是4,但’abcde’编辑为’bcdea’的最小编辑距离是2。
最优子结构与状态转移方程
\(
min\begin{cases}
d(i,j-1) + W_{ins} \\ \\
d(i-1,j) + W_{del} \\ \\
d(i-1,j-1) + W_{rep}\cdot w(i,j) \\ \\
d(i-1,j-1) + W_{ins}\cdot w(i,j) + W_{del}\cdot w(i,j)
\end{cases}
\)
设\(d(i,j)\)是将\(s_1[1..i]\)变为\(s_2[1..j]\)的最小距离。\(s_1[i]=s_2[j]\)时\(w(i,j)=0\),否则\(w(i,j)=1\)。
定理c) 设\(i\geq 0\),有\(d(0,i) = i\cdot W_{ins}\),\(d(i,0) = i\cdot W_{del}\)。
该定理比较简单,它是最小编辑距离问题的状态转移方程的边界条件。
定理d) 设\(i\geq 1, j\geq 1\),\(d(i,j)\)等于上述表达式。
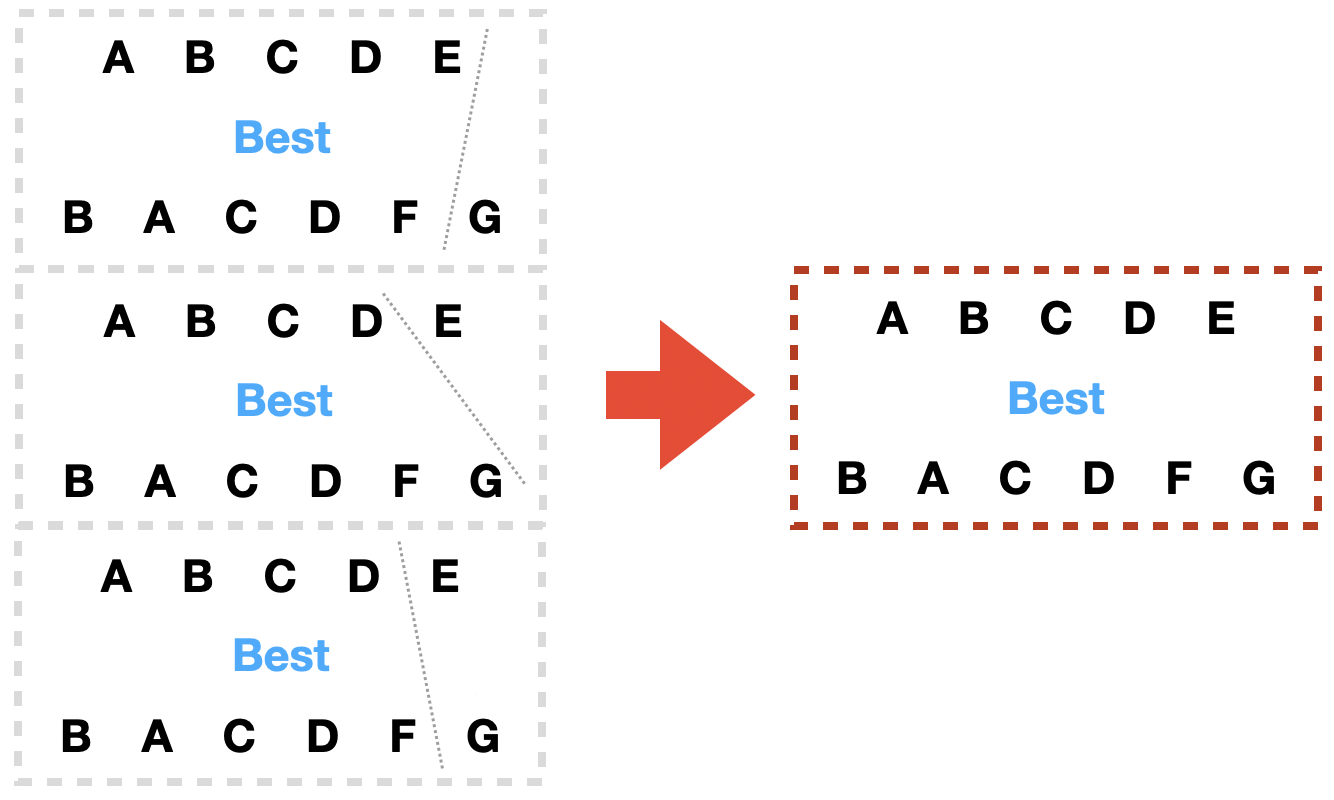
证明:先观察上图中的例子,上图左边的3个图都包含虚线,虚线左右两边都是能表示最小编辑距离的“划分图”(蓝线没有画出),所以这里的虚线表示把左右两边进行“拼接”。这样一来这3个图表示了3个“拼接图”,这3个“拼接图”都可以作为右图的“划分图”,下面证明这3个“拼接图”一定有至少1个图对应最小编辑距离。
不妨想象已得到了1个右图对应的最小编辑距离的“划分图”,这个“划分图”的两行的最末字符分别是E/G。E/G上的“蓝线”可分为这几种情况:”E和G都不被连接”,”E和G被互连接”,”E连向非G(此时由于蓝线不能交叉,G上没有蓝线)”,”G连向非E(此时由于蓝线不能交叉,E上没有蓝线)”。
此时继续想象把左边3张图某个图的虚线“移”过来,那么左边3张图的3种虚线至少有1个不会与这个“划分图”中的蓝线相交,把这个图计为P。此时等于找到了1个“分割”,根据推论b,分割得到的2个“子划分图”都对应了最小编辑距离,且二者之和等于当前“划分图”对应的最小编辑距离。也就是说这2个“子划分图”对应的“子问题”的解的和等于“当前问题”的解,即P图对应的编辑距离等于“当前问题”的解。此时左图中除了P还有2个图,这2个图同样对应了“当前问题”的编辑距离,但不一定是最小编辑距离。综上,上图左边的3个图对应了3个编辑距离值,其中的最小值就是原问题的解。
最后确定数值关系,左边3张图中虚线左边对应的编辑距离从上到下等于\(d(i,j-1),d(i-1,j),d(i-1,j-1)\)。虚线右边从上到下第1个等于\(W_{ins}\),第2个等于\(W_{del}\),第3个情况比较复杂,当\(s_1[i]=s_2[j]\)时等于0,当\(s_1[i]\neq s_2[j]\)时由于无法排除\(W_{ins} + W_{del} \leq W_{rep}\)的情况,所以等于\(min\{(W_{ins} + W_{del}), W_{rep}\}\)。最后简单整理这些关系就能得到原式。
把定理(c)(d)作为状态转移方程,按常规顺序填写用于DP的二维数组即可。由于二维数组有大概\(|s_1|\cdot |s_2|\)个位置需要填写,每次计算填写值需\(O(1)\)代价,故算法的代价是\(O(|s_1|\cdot |s_2|)\)。
算法实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | def _med(source, target, _insert, _delete, _replace): I = range(len(source)+1) J = range(len(target)+1) dp = [ [ None for j in J ] for i in I ] for i in I: for j in J: if i == 0: dp[i][j] = j * _insert if j == 0: dp[i][j] = i * _delete for i in I: for j in J: if i > 0 and j > 0: flg = source[i-1] == target[j-1] dp[i][j] = min( dp[i][j-1] + _insert, dp[i-1][j] + _delete, dp[i-1][j-1] + ( 0 if flg else _replace ), dp[i-1][j-1] + ( 0 if flg else (_insert + _delete) ), ) return dp[-1][-1] def levenshtein(s1,s2): return _med(s1,s2,1,1,1) def hamming(s1,s2): bound = 1 + max(len(s1),len(s2)) v = _med(s1,s2,bound,bound,1) return float('inf') if v >= bound else v def lcs(s1,s2): bound = 1 + len(s1) + len(s2) return _med(s1,s2,1,1,bound) |