TREAP树(树堆)
1980年Jean Vuillemin在解决范围搜索的问题时提出笛卡尔树,其特点是节点包含2个关键字。之后Edward McCreight提出一种基于笛卡尔树的结构并称之为Treap树,这是Tree和Heap的合成词,所以Treap也译为树堆。1989年Raimund Seidel和Cecilia R. Aragon利用带随机化策略的Treap树实现了BST的功能,在此之后Treap树一般用于指代这种结构。Treap树不是严格意义的自平衡二叉树,但其相比BST能在更一般的条件下保证二叉树的期望高度是\(O(\lg{n})\)。这里直接给出Treap树的定义,首先Treap节点相比前文的BST节点要额外存储一个堆关键字\(hkey\),Treap树的运算功能和前文的BST一致,但每次运算开始前后除了要保证二叉树是BST还要保证任意节点的\(hkey\)都不大于其所有后代的\(hkey\),最后规定Treap树的运算为如下的步骤:
1) \(find(k)\):与BST的\(find(k)\)完全一致(按之前讨论BST的文章中的步骤);
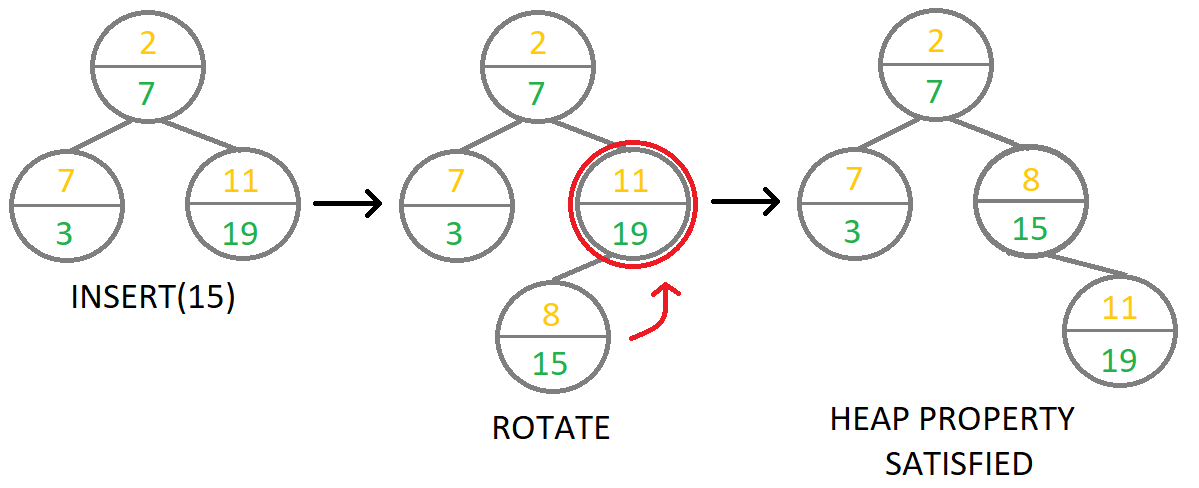
2) \(insert(k)\):先执行BST的\(insert(k)\)得到新节点\(x\)(按之前讨论BST的文章中的步骤),并初始化\(x\)的\(hkey\)为一个尽可能大的范围内的随机数(仅为了降低其重复的概率)。然后开始一个迭代过程,在每轮迭代中,若此时\(x\)无父亲或\(x\)的\(hkey\)不小于其父亲的,则退出迭代,否则通过一次左旋转或右旋转使\(x\)取代其父亲的位置,然后继续下一轮迭代;
3) \(remove(k)\):先执行BST的\(find(k)\)得到待删除节点\(x\)(按之前讨论BST的文章中的步骤),若查找失败则退出,否则开始一个迭代过程,在每轮迭代中,若\(x\)是叶节点,则删除\(x\)并退出迭代,否则找到此时\(x\)的\(hkey\)较小的孩子\(x’\),通过一次左旋转或右旋转使\(x’\)取代\(x\)的位置,然后继续下一轮迭代;
不难验证上述步骤能正确维护“任意节点的\(hkey\)都不大于其所有后代的\(hkey\)”。注意到Treap树有一定概率能在每次运算后都刚好是“链表”形态,所以其不可能是严格意义的自平衡二叉树,其各个运算也不可能有\(O(\lg{n})\)的摊还代价。另外上述定义所给出的Treap树也称为小根堆Treap树,若修改上述运算步骤使其维护“任意节点的\(hkey\)都不小于其所有后代的\(hkey\)”,则称之为大根堆Treap树。实际堆(heap)本身也是种数据结构,大根堆和小根堆都是关于堆的概念,之后有文章专门讨论堆。
TREAP树的时间复杂度
下面从统计的角度分析Treap树的各个运算的代价。首先假定\(hkey\)的取值范围大到\(hkey\)不可能重复,并且\(key\)也不重复。考虑对空树\(T\)执行由上述运算所组成的运算序列,可以认为该运算序列是已知的,于是在执行完运算序列后\(T\)中的所有节点及其它们的\(key\)就都是已知的,但由于\(hkey\)值是随机的,所以可认为\(T\)的形态是未知的,但此时还是能按照\(key\)值的升序将\(T\)中的所有节点依次计为\(x_1,x_2…x_n\)(\(n\geq 2\))。接下来通过给出一组命题并证明这些命题来讨论:
a1) 若\(i\neq j\)且\(i,j\)的值都属于\([1,n]\)则有“\(x_i\)是\(x_j\)的祖先 \(\Leftrightarrow\) \(x_i\)是\(x_{min(i,j)},x_{min(i,j)+1}…x_{max(i,j)}\)中\(hkey\)最小的节点”;
证明:将问题划为如下情况讨论:
1) \(x_i\)是树根:显然(a1)左右两边都成立;
2) \(x_j\)是树根:显然(a1)左右两边都不成立;
3) \(x_i,x_j\)都不是树根:继续分情况讨论如下:
3.1) \(x_i\)非\(x_j\)的祖先且\(x_j\)非\(x_i\)的祖先:设\(x_k\)是\(x_i,x_j\)的最近公共祖先,则\(x_k\)的\(hkey\)一定小于\(x_i\)的\(hkey\)。注意到\(x_i,x_j\)一定分别位于\(x_k\)的两个子树,否则\(x_k\)就不是最近的公共祖先,故\(min(i,j)<k<max(i,j)\)。综上(a1)左右两边都不成立;
3.2) \(x_j\)是\(x_i\)的祖先:根据BST的性质,若\(j>i\)则\(x_{min(i,j)}…x_{max(i,j)-1}\)都在\(x_j\)左子树,若\(i>j\)则\(x_{min(i,j)+1}…x_{max(i,j)}\)都在\(x_j\)右子树。无论如何\(x_j\)都是\(x_{min(i,j)},x_{min(i,j)+1}…x_{max(i,j)}\)中\(hkey\)最小的节点。综上(a1)左右两边都不成立;
3.3) \(x_i\)是\(x_j\)的祖先:根据BST的性质,若\(i>j\)则\(x_{min(i,j)}…x_{max(i,j)-1}\)都在\(x_i\)左子树,若\(j>i\)则\(x_{min(i,j)+1}…x_{max(i,j)}\)都在\(x_i\)右子树。无论如何\(x_i\)都是\(x_{min(i,j)},x_{min(i,j)+1}…x_{max(i,j)}\)中\(hkey\)最小的节点。综上(a1)左右两边都成立;
由于在任何情况下(a1)的左右两边要么同时成立要么同时不成立,所以(a1)的左右两边是一对充要条件。
a2) 此时\(T\)中的任意节点\(x_k\)的期望高度都以\(2\ln{n}+1\)为上界;
证明:设\(i\neq j\)且\(i,j\)的值都属于\([1,n]\),\(Y_{i,j}\)为一组指示器型随机变量,若\(x_i\)是\(x_j\)的祖先则\(Y_{i,j}=1\),否则\(Y_{i,j}=0\)。注意到节点的高度为该节点的祖先数+1,所以\(x_k\)的高度\(H_k = \sum_{x=1}^{k-1} Y_{x,k} + \sum_{x=k-1}^{n} Y_{x,k} + 1\),对该式两边求期望并利用期望的线性性可得\(E[H_k] = \sum_{x=1}^{k-1} E[Y_{x,k}] + \sum_{x=k+1}^{n} E[Y_{x,k}] + 1\)。根据(a1)有\(E[Y_{i,j}]\)等于“\(x_i\)是\(x_{min(i,j)}…x_{max(i,j)}\)中\(hkey\)最小的节点”的概率,由于每个\(hkey\)都是随机和独立的,故\(x_{min(i,j)}…x_{max(i,j)}\)中每个节点都等可能的会成为它们中\(hkey\)最小的节点,于是可得到\(E[Y_{i,j}]=\frac{1}{|i-j|+1}\),进而有\(E[H_k]=\sum_{x=1}^{k-1} \frac{1}{|x-k|+1} + \sum_{x=k+1}^{n} \frac{1}{|x-k|+1} + 1 = \sum_{y=2}^{k} \frac{1}{y} + \sum_{y=2}^{n-k+1} \frac{1}{y} + 1\)。做进一步的放缩并利用积分可得到\(E[H_k] \leq 2 \sum_{y=2}^{n} \frac{1}{y}+1 < 2\int_{1}^{n} \frac{1}{y}dy + 1 = 2\ln{n} + 1\)。
至此根据(a2)可确定\(T\)的期望高度也以\(2\ln{n}+1\)为上界,并且对于\(n=1\)这个界同样也是正确的。换句话说如果从空树开始不停执行上述运算,则每次运算的期望代价都是\(O(\lg{N})\),其中\(N\)是每次运算开始时的二叉树节点数。另外前面为方便讨论假设\(key\)不重复,但即使\(key\)重复也不影响上述分析的正确性,简单来说如果对空树执行运算序列\(L\)后会出现重复的\(key\),则必然存在与\(L\)步骤“等价”且不导致重复\(key\)的运算序列,换句话说重复的\(key\)并不能实际影响到运算步骤本身。
总结与实现
Treap树的运算步骤本身很简单,唯一要注意的是在程序中无法保证\(hkey\)重复的概率为0,通常会用2种方法生成\(hkey\),一种是在整个int数据类型的范围中取值,另一种是生成随机浮点数。最后给出Treap树的程序实现如下,为了方便这里直接使用Python内置的random.random生成0~1之间的随机浮点数。其他未提到的细节见程序与注释。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 | from random import random class Node: def __init__(self, key): self.key = key self.parent = None self.left = None self.right = None class Treap: def __init__(self): self.root = None def _rightRotate(self, n): m = n.left n.left = m.right m.right = n if not n.parent: self.root = m elif n.parent.left is n: n.parent.left = m else: n.parent.right = m m.parent = n.parent n.parent = m if n.left: n.left.parent = n def _leftRotate(self, n): m = n.right n.right = m.left m.left = n if not n.parent: self.root = m elif n.parent.left is n: n.parent.left = m else: n.parent.right = m m.parent = n.parent n.parent = m if n.right: n.right.parent = n def _bstFind(self, k): root = self.root while root: if k == root.key: return root elif k < root.key: root = root.left else: root = root.right return None def find(self, k): return self._bstFind(k) def _bstInsert(self, k): if not self.root: self.root = Node(k) return self.root root = self.root while root: if k < root.key: if not root.left: root.left = Node(k) root.left.parent = root return root.left root = root.left else: if not root.right: root.right = Node(k) root.right.parent = root return root.right root = root.right def insert(self, k): x = self._bstInsert(k) x.hkey = random() # 初始化hkey while x.parent and x.parent.hkey > x.hkey: if x.parent.left is x: self._rightRotate(x.parent) else: self._leftRotate(x.parent) return x def remove(self, k): x = self._bstFind(k) if not x: return x while x.left or x.right: if not x.left: self._leftRotate(x) elif not x.right: self._rightRotate(x) elif x.left.hkey > x.right.hkey: self._leftRotate(x) else: self._rightRotate(x) if x.parent: if x.parent.left is x: x.parent.left = None else: x.parent.right = None x.parent = None else: self.root = None return x |