基于最大流的算法
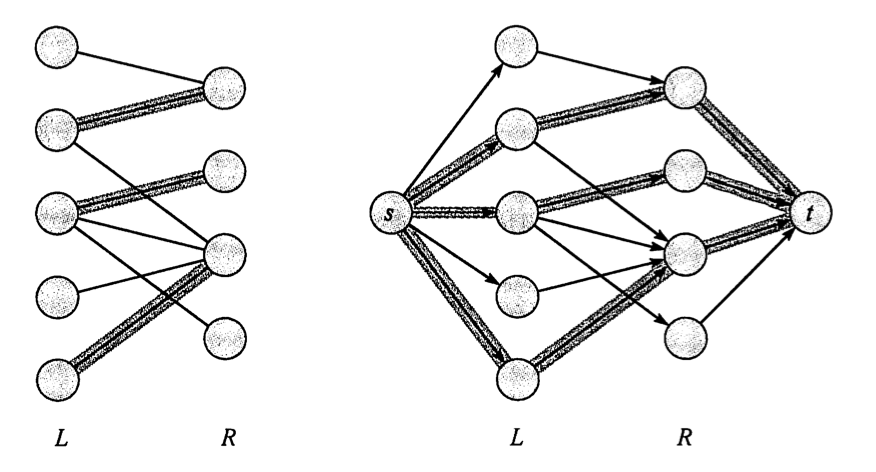
定义\(G’=(V’,E’)\)为二分图\(G=(V,E)\)与其顶点划分\((L,R)\)所给定的流网络,其中\(V’=V\bigcup \{s,t\}\),即源\(s\)与汇\(t\)是不属于\(V\)的新顶点。横跨\((L,R)\)的无向边(所有\(E\))是\(E’\)中\(L\)到\(R\)的有向边,\(E’\)需额外加入\(s\)到\(L\)所有节点的边,\(R\)所有节点到\(t\)的边。流网络的每个边的容量都是1,定义1值流\(f\in \{0,1\}\),给出关于\(G\)与\(G’\)的关键引理:
a) \(G\)存在匹配\(M\),则\(G’\)存在1值流\(f\),其中\(|f|=|M|\);
对任意边\((u,v)\in M\),定义流\(f(s,u)=f(u,v)=f(v,t)=1\)即可,显然\(|f|=\sum f(s,u) = |M|\)。
b) \(G’\)存在1值流\(f\),则\(G\)存在匹配\(M\),其中\(|f|=|M|\);
对于\(L\)的顶点\(u\),其仅有入边\((s,u)\),故到达\(u\)的流量只能为1,此时其仅能通过其中一条出边把流量1发出。同理对于\(R\)的顶点\(v\)其仅有出边\((v,t)\),故其仅接受1条入边流入1。对所有\(f(u,v)=1\),\(u\)不重复,\(v\)不重复,\(L\)与\(R\)不相交,故\(M=\{(u,v)| f(s,u)=f(u,v)=1\}\),\(|M|=|f|\)。
根据之前文章,FF法可求得任何整数容量流网络的最大流,且求得的最大流满足所有边的流都为整数,这样FF法对该问题会收敛。如果采用普通的FF算法实现,其时间复杂度为\(O(|E||V|)>O(|E||M|)=O(|E||f^*|)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 | class NetworkFlow: def __init__(self,s,t): self.s = s self.t = t self.c = {} self.f = {} self.cf = {} def add_edge(self,u,v,c): if None==self.c.get(u): self.c[u] = {} self.f[u] = {} self.cf[u] = {} self.c[u][v] = c self.f[u][v] = 0 self.cf[u][v] = c if None==self.c.get(v): self.cf[v] = {} self.cf[v][u] = 0 def has_edge(self,u,v): return self.c.get(u)!=None and self.c[u].get(v)!=None and self.c[u][v] > 0 def residual_has_edge(self,u,v): return self.cf.get(u)!=None and self.cf[u].get(v)!=None and self.cf[u][v] > 0 def dfs(self,u,visited,pi): if None!=self.cf.get(u): for v in self.cf[u].keys(): if v not in visited and self.residual_has_edge(u,v): pi[v] = u if v == self.t: return visited.add(v) self.dfs(v,visited,pi) def dfs_path(self): pi = {} self.dfs(self.s,{self.s},pi) v = self.t path = [] while pi.get(v)!=None : u = pi[v] path.append((u,v)) v = u path.reverse() return path def updata_f(self,path): cp = float('inf') for u,v in path: cp = min(cp,self.cf[u][v]) for u,v in path: if self.has_edge(u,v): self.f[u][v] += cp else: self.f[v][u] -= cp def updata_gf(self): for u in self.cf.keys(): for v in self.cf[u].keys(): if self.has_edge(u,v): self.cf[u][v] = self.c[u][v] - self.f[u][v] elif self.has_edge(v,u): self.cf[u][v] = self.f[v][u] else: self.cf[u][v] = 0 def ford_fulkerson(self): while True: path = self.dfs_path() if not path: break self.updata_f(path) self.updata_gf() def max_flow_value(self): u = self.s val = 0 if self.c.get(u)!=None: for v in self.c[u].keys(): val += self.f[u][v] return val def maximum_match(l2r): n = NetworkFlow('s','t') r = set() for u in l2r.keys(): n.add_edge('s',u,1) for v in l2r[u]: n.add_edge(u,v,1) r.add(v) for u in r: n.add_edge(u,'t',1) n.ford_fulkerson() print(n.max_flow_value()) |
匈牙利算法(Hungarian’s Algorithm)
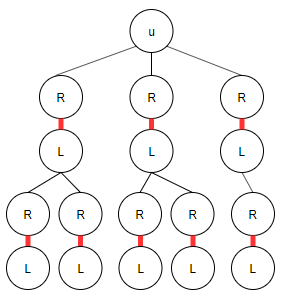
首先给出没有明确步骤的“匈牙利方法”,其为Berge定理的直接结论,故其正确:
1) 初始化空匹配\(M\);
2) 找到从\(L\)出发关于\(M\)的增广路\(p\)并进入(3),找不到说明当前为最大匹配,算法结束;
3) 利用增广路\(p\)扩大\(M=M\oplus p\),回到步骤(2);
该策略转化为算法本身不困难,关键是如何转化为更高效的算法,下面给出两个我自己归纳的引理:
a) 若从\(L\)未匹配点\(u\)出发无增广路,则\(u\)出发的所有交错路顶点都不在\(L\)出发的任何增广路上;
如上图用\(u\)的交错路BFS树验证这点,BFS树显然包含所有交错路。其中黑边为非匹配边,红边为匹配边,自顶向下每层交替的为\(LR\)顶点。当BFS从\(L\)的\(x\)发现\(R\)的\(y\)时,\(y\)匹配边另一端属于\(L\)的\(z\)一定会在BFS树中,由于\(R\)到\(L\)的边只能通过唯一的匹配边发现,如果\(z\)没有被BFS从\(y\)发出的匹配边\((y,z)\)发现,那么\(y\)不可能是首次被发现,这导致与BFS性质矛盾。然后分析BFS树中未出现的从\(L\)到\(R\)的边,显然任何从\(L\)到\(R\)的边所抵达的顶点都在该BFS树上,但是未出现的从\(R\)到\(L\)的边却可能抵达该BFS树以外的顶点,但这并不影响我们得出上述结论。假设存在从\(L\)出发的增广路\(p\)包含上述BFS树的顶点,由于其是“从L出发”的,所以\(p\)从左到右看来,其任何\(R\)顶点的后继只能为其匹配边另一端属于\(L\)的顶点。若\(p\)从左到右第1个属于该BFS树的顶点是\(R\)的顶点,由于匹配边唯一,其后继必是BFS树中的\(L\)顶点,然后这个顶点的后继又只能在该BFS树中…若\(p\)从左到右第1个属于该BFS树的顶点是\(L\)的顶点同理,所以这种情况无论如何都找不到非匹配点。
b) 若从\(L\)未匹配点\(u\)出发无增广路,任意次扩大匹配后\(u\)出发的所有交错路顶点都不在\(L\)出发的增广路上;
设当前匹配有\(L\)发出的增广路\(p\),若用其增广将只改变\(p\)中的边的“匹配-非匹配”关系,即\(p\)中的顶点的“匹配-非匹配”关系。根据(a)可知\(p\)所有顶点都不在\(u\)树上,故扩大后\(u\)仍是未匹配点,且从\(u\)出发得到的BFS树与当前相同。最后可“循环不变”将结论推广到任意次扩大匹配后。
综上(a)(b)可得基于BFS的算法,从\(L\)选未匹配点BFS交错路,如果没有发现增广路,将BFS树的全部顶点从二分图中删除。如果发现增广路,则利用该增广路增广,注意此时不删除任何BFS的顶点,然后循环的从\(L\)选未匹配点BFS交错路……由于\(L\)中的每个顶点无论能否BFS到增广路,都仅发生一次BFS,故代价为\(O(|V||E|)>O(|L||E|)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 | from collections import deque def copy(l_to_r): g = {} for u in l_to_r: g[u] = set() for v in l_to_r[u]: g[u].add(v) return g def reverse(l_to_r): r_to_l = {} for u in l_to_r.keys(): for v in l_to_r[u]: if v not in r_to_l: r_to_l[v] = set() r_to_l[v].add(u) return r_to_l def augment(path,l_match_r,r_match_l): while path: l = path.pop() r = path.pop() l_match_r[l] = r r_match_l[r] = l def cutoff(l_to_r,r_to_l,r_visited): while len(r_visited)>0: r = r_visited.pop() for l in r_to_l[r]: l_to_r[l].remove(r) def bfs(u,l_to_r,r_to_l,l_match_r,r_match_l): if u in l_match_r: return queue = deque([u]) prev = {u: None} r_visited = set() while len(queue)>0: u = queue.popleft() if u in l_to_r: for v in l_to_r[u]: if v not in r_visited: r_visited.add(v) if v in r_match_l: queue.append(v) prev[v] = u else: path = [v,u] while prev[u]: path.append(prev[u]) u = prev[u] augment(path,l_match_r,r_match_l) return else: queue.append(r_match_l[u]) prev[r_match_l[u]] = u cutoff(l_to_r,r_to_l,r_visited) return def hungary(l_to_r): l_to_r = copy(l_to_r) r_to_l = reverse(l_to_r) l_match_r = dict() r_match_l = dict() for u in l_to_r.keys(): bfs(u,l_to_r,r_to_l,l_match_r,r_match_l) return l_match_r |
Hopcroft-Karp算法
首先是给出关于算法正确性与时间复杂度的引理如下:
a) 任意匹配\(M\)都存在无公共顶点的增广路\(P_1…P_n\),使\(M\oplus (P_1\bigcup…P_n)\)为最大匹配;
利用之前文章中Berge定理的(2)与(4)容易验证。
b) 对任意匹配\(M\),若\(M\)的最短增广路长度为\(l\),则最大匹配边数至多为\(|M| + \frac{|V|}{l+1}\);
\(M\)最短增广路顶点数为\(l+1\),故\(M\)无公共顶点的增广路集的元素数存在上界\(\frac{|V|}{l+1}\),利用(a)可得最大匹配数存在上界\(|M|+\frac{|V|}{l+1}\)。
c) \(S=\{P_1,P_2,…,P_k\}\)为无公共顶点的\(M\)极大最短增广路集。极大指\(S\)确定了元素\(P_1,…,P_k\)后,无法再找到最短的且与\(P_1,…,P_k\)无公共点的增广路,极大非最大。令\(l\)为最短增广路长度。令\(M’=M\oplus(P_1\bigcup P_2\bigcup …P_k)\),\(P\)是\(M’\)的1个最短增广路。在此之下有\(|P|>l\)的结论;
i) 设\(P\)与\(S\)无公共顶点,则\(P\)的边数大于\(l\);
根据之前文章对Berge定理的讨论,可直观的直接分析,对于增广前的\(M\)与增广后的\(M’\),\(S\)外的边是匹配边还是非匹配边是不变的。因为\(P\)所有点都不在其中,所有边都不在其中,所以\(P\)是\(M\)与\(M’\)的增广路,如果\(P\)的边数等于\(l\),则\(P\)可加入\(S\),与\(S\)极大矛盾。
ii) 设\(P\)与\(S\)有公共顶点,则\(P\)的边数大于\(l\);
1) 令\(M”=M’\oplus P\),由对称差结合律\((M\oplus M’)\oplus P=M\oplus (M’\oplus P)=M\oplus M”\);
2) 根据之前文章Berge定理(2)有\(|M”|-|M|=k+1\),根据Berge定理(4)可知\(M\oplus M”\)至少有\(k+1\)个关于\(M\)的无公共顶点的增广路,无公共点意味着无公共边,根据上文关于\(M\)的最短增广路长度为\(l\),故\(|M\oplus M”|\geq (k+1)l\);
3) 证明\(M\oplus M’=P_1\bigcup P_2\bigcup …P_k\)。显然\(M-M’\)即是无公共顶点的\(P_1\bigcup P_2\bigcup …P_k\)的所有匹配边,而\(M’-M\)是其所有非匹配边,故\((M-M’)\bigcup (M’-M)=P_1\bigcup P_2\bigcup …P_k\)命题得证;
4) 整理上述有\(| (P_1\bigcup P_2\bigcup …P_k)\oplus P |\geq (k+1)l\),由对称差性质有\(| (P_1\bigcup P_2\bigcup …P_k) | + |P| \geq| (P_1\bigcup P_2\bigcup …P_k)\oplus P |\)。再进行简单的整理可得不等式\(| (P_1\bigcup P_2\bigcup …P_k) | + |P| \geq | (P_1\bigcup P_2\bigcup …P_k)\oplus P | \geq (k+1)l \);
5) 分析上式取等号的情况,此时\(P\)的长度为\(l\)且与\(P_1\bigcup …P_k\)无公共边。无公共边意味着在增广步骤\(M’=M\oplus(P_1\bigcup P_2\bigcup …P_k)\)发生前后,\(P\)中的所有边是\(M\)匹配边还是\(M\)非匹配边是不变的,故\(P\)也是\(M\)的增广路。再引入题设中\(P\)与某个\(P_i\)有公共点的条件,若\(P\)与\(P_i\)的公共点是这两个增广路首尾的\(M\)非匹配点,这导致\(P\)不能是\(M’\)的增广路,引发矛盾。若\(P\)与\(P_i\)的公共点是\(M\)匹配点,由于增广路的任何匹配点连接的匹配边都在该增广路上,\(P\)与\(P_i\)将存在公共边,引发矛盾。故上式不能取等号,\(| (P_1\bigcup P_2\bigcup …P_k) | + |P| > (k+1)l \),\(|P|>l\)。
然后可以给出Hopcroft-Karp算法的大致流程如下:
1) 初始化二分图\(G\)的空匹配\(M\);
2) 求\(M\)的一个无公共顶点的极大最短增广路集\(P_1,P_2,…,P_k\),若该集合为空则\(M\)为最大匹配,算法退出;
3) 执行多路增广\(M=M\oplus P_1\bigcup …P_k\),并回到(2);
其正确性容易被之前对Berge定理的讨论所验证。设上述流程对\(M\)执行了\(\sqrt{|V|}\)次多路增广,那么此时\(M\)的最短增广路长度至少为\(\sqrt{|V|}\),最大匹配数为\(|M| + \frac{|V|}{l+1}=\sqrt{|V|} + \frac{|V|}{\sqrt{|V|}+1}=O(\sqrt{|V|})\),故步骤(2)总次数有上界\(O(\sqrt{|V|})\)。接下来的是如何通过算法求某个无公共顶点的极大最短增广路集。这里先给出这样1种特殊BFS步骤:
1) 计当前匹配下\(L\)中的任意未匹配点为\(u\),初始化队列\(u\in Q\),数组\(D[u]=0\);
2) 用\(Q\)执行与上文匈牙利算法相似的“交错路BFS”,在\(u\)下通过\((u,v)\)首次访问\(v\)时,维护\(D[v]=D[u]+1\);
3) 在(2)中的交错路BFS中在首次访问到\(v\)时,若发现是\(v\)是\(R\)中的未匹配点,那么对于该尚未结束的交错路BFS,在\(v\)所在层的全部顶点的子BFS结束后,令整个交错路BFS停止退出;
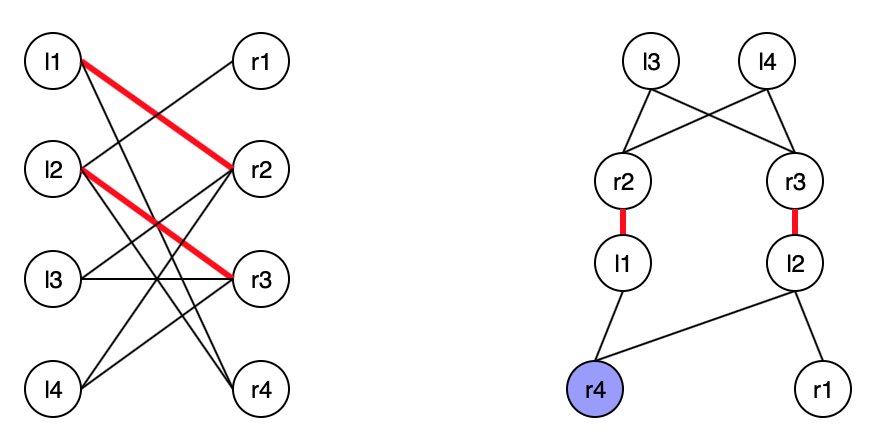
如上图,紫色是首个发现的\(R\)未匹配点,\(D\)给出对原图部分节点\(u\)的“分层”,1层是所有\(L\)的未匹配点,2层是1层所有出边可达的顶点,3层是2层所有顶点匹配边的另一端,4层是3层所有出边可达且未出现的顶点,5层是4层所有顶点匹配边的另一端……然后对上述顶点的“分层”加入原二分图的图边,1层与2层间加入所有1层顶点与2层顶点间的非匹配边,2层与3层间加入所有2层与3层顶点间的匹配边……然后归纳这样所得到的图\(H\)的性质,\(H_i\)表示\(i\)层所有顶点:
d) 若从\(u\in H_1\)出发可达\(v\),则\(H_1\)到\(v\)的最短交错路长度为\(D[v]\);
e) 若从\(u\in H_1\)出发可达\(v\)且\(v\)为首个发现的\(R\)未匹配点,则最短增广路长度为\(D[v]\);
f) 若从\(u\in H_1\)出发的首个增广路长度为\(d\),则\(H\)包含的增广路为从\(H_1\)出发且长度为\(d\)的所有增广路;
根据上述可直观验证的几条性质,任何无公共顶点的极大最短增广路集,其增广路都是\(H\)上的增广路,其边都是\(H\)上的边,下面通过另一种特殊的DFS从\(H\)求出1个无公共点的极大最短增广路集:
1) 初始化空的无公共顶点的极大最短增广路集\(S\);
2) 遍历\(R\)的未匹配顶点,每次遍历都执行1次步骤(3),这里把遍历到的顶点计为\(u\);
3) 若有\(D[u]\),则\(H\)存在\(H_1\)到\(u\)的最短增广路,反向的从\(u\)执行DFS,若到达\(H_1\),则退出DFS,将该增广路\(p\)加入\(S\),把\(p\)的顶点与关联边从\(H\)删除。若无\(D[u]\)或不可达\(H_1\),不做任何操作;
4) 遍历结束则\(S\)为一个无公共顶点的极大最短增广路集,用其增广原匹配;
这样得到的\(S\)必然是极大的,如果\(S\)还可被加入与其无公共顶点的增广路,那么其必然在循环的某个阶段被发现。对于上述特殊BFS而言,其仅到达原二分图的每个图边常数次,故代价为\(O(|E|)\),但对上述特殊DFS而言,根据其流程,其是对每个\(R\)未匹配点都执行“一定程度上独立”的DFS,故不能确认其代价是\(O(|E|)\),下面分析其性质:
g) 若从\(R\)未匹配点\(u\)执行DFS,最终不可达\(H_1\),则该DFS树的任何顶点都不可达\(H_1\);
h) 若从\(R\)未匹配点\(u\)执行DFS,最终到达\(H_1\),此时从\(u\)到其的路径上的所有子DFS都还不算是结束,那么对于当前所有子DFS都已结束的顶点,其都不可达\(H_1\);
由于(g)(h)且原DFS发现增广路后会删去增广路在\(H\)的顶点,可以发现可以在原DFS的基础上把删边策略改进为对于每个\(R\)未匹配点的DFS,无论是其未发现增广路,或是其发现了增广路并停止DFS返回,在DFS结束后都可以把其途径的所有顶点都删除(染色),这样一来每个边至多访问常数次,代价为\(O(|E|)\)。算法总代价\(O(|E|\sqrt{|V|})\),讨论完毕。
这个算法和流网络的Dinic算法很相似,其都是先构造层次图然后连续找最短增广路并增广,事实上如果把二分图构造成流网络,然后执行Dinic算法,其代价也是\(O(|E|\sqrt{|V|})\),这一点就不讨论了。Hopcroft-Karp算法是截至目前人们发现的最快的算法。另外对于Hopcroft-Karp与匈牙利算法,都可做简单的贪心优化,即不从空匹配开始增广,而是先遍历二分图尝试把遍历到的边都加入匹配,再从这个匹配上开始增广。给出该算法的Python实现如下,一定要小心处理好其中用于生成分层图的特殊BFS,分层图可以看作是有重复节点的一组交错路BFS树,所以不能像通用BFS那样要求节点只能“被发现”1次(遍历),所以要特殊的处理好“当前已发现顶点”集合。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 | def bfs(l_to_r,l_match_r,r_match_l): layer = set(l_to_r.keys()) - set(l_match_r.keys()) l_prev = {} r_prev = {} r_visited = set() r_unmatched = set() while True: current_r_visited = set() tmp = set() for u in layer: for v in l_to_r[u]: if v not in r_visited: current_r_visited.add(v) if v not in r_prev: r_prev[v] = set() r_prev[v].add(u) if v not in r_match_l: r_unmatched.add(v) else: tmp.add(v) if len(r_unmatched) > 0: return r_unmatched,l_prev,r_prev if not current_r_visited: return False for r in current_r_visited: r_visited.add(r) layer = set() for v in tmp: l_prev[r_match_l[v]] = v layer.add(r_match_l[v]) def dfs(r,l_prev,r_prev,l_visited): for l in r_prev[r]: if l not in l_visited: l_visited.add(l) if l not in l_prev: return [l,r] rr = l_prev[l] path = dfs(rr,l_prev,r_prev,l_visited) if path: path.append(l) path.append(r) return path def hopcroft_karp(l_to_r): l_match_r = {} r_match_l = {} while True: result = bfs(l_to_r,l_match_r,r_match_l) if not result: return l_match_r r_unmatched,l_prev,r_prev = result paths = [] l_visited = set() for r in r_unmatched: p = dfs(r,l_prev,r_prev,l_visited) paths.append(p) for p in paths: while p: r = p.pop() l = p.pop() l_match_r[l] = r r_match_l[r] = l |