无向图的覆盖集
点覆盖:无向图的点覆盖是顶点集的子集,边集中的每个边都至少有1个端点位于点覆盖;
点覆盖数:点覆盖中的元素数目;
最小点覆盖:元素数目最小的点覆盖;
边覆盖:无向图的边覆盖是边集的子集,顶点集中的每个顶点都为边覆盖中至少1个边的端点;
边覆盖数:边覆盖中的元素数目;
极小边覆盖:若一个边覆盖的任何真子集都不是边覆盖,则称其为极小边覆盖。这里考虑关于无向图\(G=(V,E)\)的两种情况,一种是存在边集\(S_1 = \{ (u,v) ~|~ v\in V-\{u\}\}\),其中\(|S_1|=|V|-1\)。另一种是存在边集\(S_2\)中每个边的每个端点只出现1次,其中\(|S_2|=\frac{|V|}{2}\)。这两种边集显然可以出现在同个无向图中,其都是极小边覆盖。
最小边覆盖:元素数目最小的边覆盖,根据极小边覆盖的定义,最小边覆盖一定属于极小边覆盖;
路径覆盖:即用若干条路径“覆盖”所有顶点,每个路径为边的序列\((v_a,v_b),(v_b,v_c)…\),路径覆盖为路径集合;
最小路径覆盖:元素数目最小的路径覆盖,这里的元素是指“一条路径”;
无向图的独立集
点独立集:无向图的点独立集是顶点集的子集,对其中任意两顶点\(u,v\)有\((u,v)\)不为图边;
独立数:点独立集中的元素数目;
团:无向图的团是顶点集的子集,对其中任意两顶点\(u,v\)有图边\((u,v)\);
团数:团中的元素数目;
边独立集(匹配):无向图的边独立集是边集的子集,对其中任意两边\((v_1,v_2)\)与\((v_3,v_4)\)有\(v_1\neq v_2\neq v_3\neq v_4\);
边独立数(匹配数):边独立集中的元素数目;
极大边独立集(极大匹配):无法再加入任何元素的边独立集;
最大边独立集(最大匹配):元素最多的边独立集,根据极大边独立集的定义,最大边独立集为极大边独立集;
二分图与二分匹配
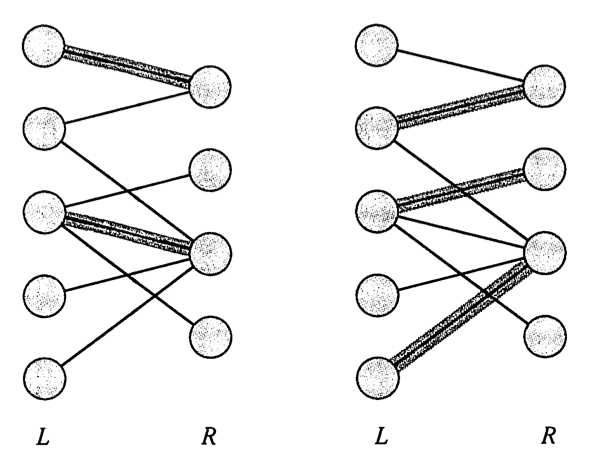
二分图(bigraph)又称二部图。对无向图\(G=(V,E)\),若\(V\)存在划分\(L,R=V-L\),使所有边只横跨\(L\)与\(R\),称\(G\)为二分图,此时若\(L\)每个顶点都与\(R\)全部顶点相连,则称\(G\)为完全二分图。另外在给定二分图\((V,E)\)时会同时给定其一个划分\((L,R)\),故二分图常被更形式化的给定为\((L,R,E)\)。
二分图的判据:无向图是二分图的充要条件是其所有环路的长度为非负偶数;
这个判据可依直观化的讨论一下,对于环路而言其长度(边数)与顶点数相等,可以任选一个顶点出发,按顺时针或逆时针的顺序来“标号”顶点为\(L\)或\(R\)表示二分图划分,由于\(L\)或\(R\)没有内部边,所以一定不能出现\(LL\)或\(RR\)这样的相邻“标号”,只能是\(LRLRLRLR….\)或\(RLRLRLRL…\),且首尾的标号是不能相同的,这就导致环路的顶点数必须为偶数,即环路的长度必须为偶数。无环任意长度的路径可按\(L,LR,LRL…\)标号,其显然不会出现相邻标号重复的现象。这里用到的“标号”这个概念和图论中的“染色”概念差不多是一个意思。
二分图的最大匹配:同上述的最大边独立集;
二分图的完备匹配:若对二分图与其划分\((L,R)\),其匹配\(M\)的端点包含全部\(L\),称\(M\)为\(L\)到\(R\)的完备匹配;
二分图的完美匹配:若对二分图的匹配\(M\),其端点包含全部顶点,称\(M\)为完美匹配;
二分图的交错路:对二分图\(G\)与其匹配\(M\),若\(G\)的路径\(p\)中\(M\)边与非\(M\)边交替出现,称\(p\)为交错路;
二分图的增广路:若交错路\(p\)的起点终点都不属于\(M\)中任何边的端点,则\(p\)为增广路(与流的增广路不太一样);
二分匹配的Berge定理
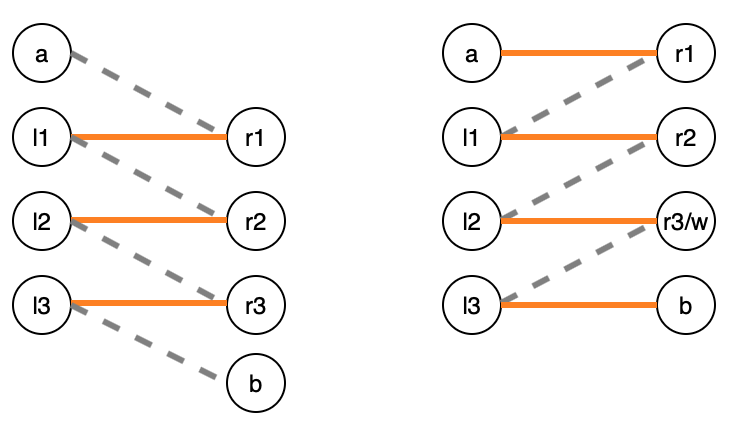
Berge定理又称增广路定理,是二分图匹配的重要定理,其也可适用于一般无向图的匹配。其图论表述为“\(M\)是\(G\)的最大匹配当且仅当\(G\)无增广路”。考虑后续将讨论二分图匹配算法,这里将Berge定理拆分讨论并加入若干推论:
1) 集合\(A\)与\(B\)的对称差被定义为\(A\bigoplus B=(A-B)\bigcup (B-A)\)。设\(M\)为二分图\(G\)的匹配,\(P\)为\(M\)的增广路。那么\(M\)与\(P\)的对称差\(M\bigoplus P\)也是二分图\(G\)的匹配,并且有\(|M\bigoplus P|=|M|+1\);
如上图,由于增广路的首尾边都是非匹配边,所以增广路的边数为奇数且非匹配边比匹配边多1条。\(P-M\)为\(P\)的非匹配边,\(M-P\)为\(P\)以外的全部匹配边,两者的交集从直观来看显然是新匹配,由于匹配边数目多1,所以新匹配的边数多1。
2) 设\(M\)为二分图\(G\)的匹配,\(P_1,P_2…P_k\)为\(M\)的\(k\)个无重复顶点的增广路,则\(M\bigoplus(P_1\bigcup P_2\bigcup …P_k)\)也是二分图\(G\)的匹配,并且有\(|M\bigoplus(P_1\bigcup P_2\bigcup …P_k)|=|M|+k\);
如上图,对于完全不相交的若干个增广路同样可以直观的得出该结论。
3) 对二分图\(G=(V,E)\)与其任意两匹配\(M_1\)与\(M_2\)。对于图\(G’=(V,M_1\bigoplus M_2)\),\(G’\)顶点的出度至多为2,边集\(M_1\bigoplus M_2\)可划成若干无公共边的路径或环路,这些路径或环路无公共顶点,且由\(M_1\)与\(M_2\)的边交替组成;
对于\(G’\)而言,其任意顶点只能同属于\(M_1\)与\(M_2\),属于\(M_1\)或\(M_2\),都不属于\(M_1\)与\(M_2\)。根据匹配的性质,其度只能为2/1/0。\(M_1\bigoplus M_2\)作为边集,其中顶点的度又至多为2,直观上\(M_1\bigoplus M_2\)如果不能被划分为互相之间没有重复顶点路径或环路,那么必然有顶点的度大于2。对于这些互相无重复顶点的路径,除首尾外的顶点,其度都为2,根据匹配的性质,这个顶点左右两端的边必然分属于\(M_1,M_2\),对于环路同理。
4) 二分图\(G\)有匹配\(|M_1|\geq |M_2|\),\(M_1\bigoplus M_2\)至少有\(|M_1|-|M_2|\)条关于\(M_2\)的无公共顶点的增广路;
利用(3)与其证明可知\(M_1\bigoplus M_2\)可划分成若干无公共顶点的路径或环路。由于所有环路顶点的度为2,故所有环路的边在\(M_1\)与\(M_2\)中各占一半。故在非环路路径中,\(M_1\)的边多了\(k=|M_1|-|M_2|\)条。由于这些路径都是交错路,故每个路径中\(M_1\)的边至多比\(M_2\)的边多1。故至少存在\(k\)个\(M_1\)的边比\(M_2\)的边多1的路径,这样的路径只能是\(M_1,M_1M_2M_1…\)的形式(即增广路)。故\(M_1\bigoplus M_2\)至少给出\(k\)个\(M_2\)的增广路。
5) \(M\)是二分图\(G\)的最大匹配当且仅当\(G\)无增广路;
充分性即(4),必要性的逆否命题显然也可利用(4)。
6) \(M\)是二分图\(G=(L,R,E)\)的最大匹配当且仅当\(G\)无从\(L\)到\(R\)的增广路;
增广路是从\(L\)到\(R\)或从\(R\)到\(L\)的,但增广路无方向故存在增广路的充要条件为存在\(L\)到\(R\)的增广路。
二分匹配的König定理
Hall定理:又称为婚姻定理。给定二分图\(G=(V,E)\)与其顶点划分\((L,R)\),用记号\(N(A)\)表示顶点集\(A\)所有顶点仅经由一条边可达的所有顶点。对于任意\(A\subseteq L\)有\(|N(A)|\geq |A|\)当且仅当从\(L\)到\(R\)存在完备匹配;
必要性易得仅证充分性,对于任意\(A\subseteq L\)满足\(|N(A)|\geq |A|\),假设从\(L\)到\(R\)的最大匹配\(M\)非完备匹配,此时\(L\)存在顶点\(u\)不在\(M\)中,根据题设有\(|N(\{u\})|\geq 1\)即\(u\)至少有1条边。对于\(u\)的任意所在边\((u,v)\),\(v\)必然是在\(M\)中的,否则\((u,v)\)可加入\(M\),导致\(M\)不是最大匹配。可发现对\(u\)出发的所有交错路,途经的都是匹配点,可归纳出“最后1个边为非匹配边的交错路,一定能在终点继续找到个匹配边”,设\(Z\)为所有交错路经过的顶点,那么\(Z\)等于所有末边为匹配边的交错路经过的顶点。对于这样的交错路,其非匹配边与匹配边的数目相等,进而得出所有这样的交错路的匹配点都均分在\(L,R\)中,所以可设\(X=Z\bigcap L,Y=Z\bigcap R\)由于\(u\in X\)故\(|X|=|Y|+1\),显然有\(Y\subseteq N(X)\)。此时从\(X\)任取顶点\(s\),然后任取\(s\)的相邻顶点\(t\)。若\((s,t)\in M\)则\(t\)一定位于\(u\)到\(s\)的交错路。若\((s,t)\notin M\)则\(u\)到\(s\)的交错路可以与\((s,t)\)形成\(u\)到\(t\)的交错路。综上对于\(s\)的任意相邻顶点,其都存在于从\(u\)出发的某个交错路上。由于\(s\)是任选的,所以\(N(X)\)存在于从\(u\)出发的某些交错路上,即\(N(X)\subseteq Y\),综上\(N(X)=Y\),进而有\(|X|=|Y|+1=|N(X)|+1>|N(X)|\)。故假设不成立,所以最大匹配\(M\)是完备匹配,由于最大匹配必然存在,完备匹配存在。
König定理:二分图的最大匹配数等于最小点覆盖数;