有根树的最近公共祖先(LCA)
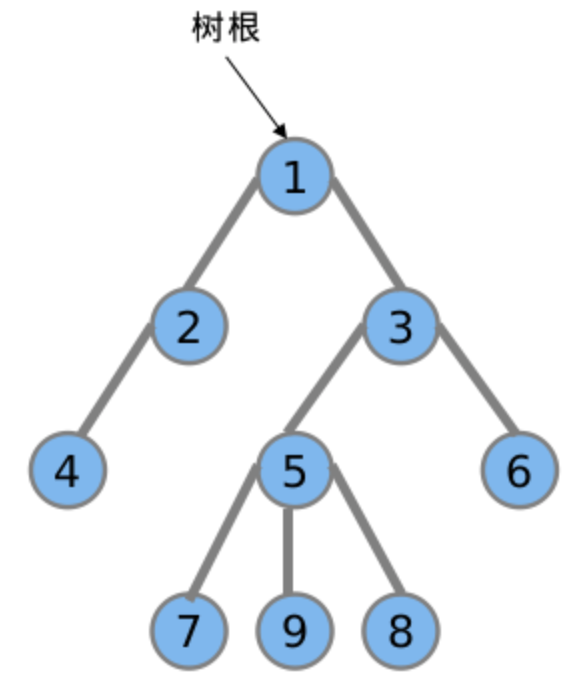
若有根树任意两点\(u,v\)都位于\(r\)点代表的子树中,则称\(r\)是\(u,v\)的公共祖先(\(r\)可等于\(u,v\)且\(u,v\)也可相等),LCA是\(u,v\)所有公共祖先中,离\(u,v\)总距离最小的(设所有边的距离为1),给出LCA的几个性质:
1) \(u,v\)的LCA是其所有公共祖先中深度最大的;
证明:设\(r\)是\(u,v\)的一个公共祖先,那么\(u,v\)距离\(r\)的总距离等于\(depth(u)-depth(r)+depth(v)-depth(r)\)。由于\(depth(u),depth(v)\)是固定的,所以\(depth(r)\)越大则说明总距离越小。
2) \(u,v\)的LCA有且仅有1个;
证明:若\(u,v\)有两个LCA,根据(1)其位于树的同层。由树性质,同层2个不同节点分别代表的子树一定无交集,导致矛盾。
这里直接给出1种求LCA的朴素算法,其流程如下:
1) 遍历树求出每个节点的深度,计为\(depth(n)\);
2) 取树中尚未求出LCA的顶点对\((u,v)\);
3) 若\(u,v\)深度相等,则计变量\(p_u=u\),\(p_v=v\)。若\(u\)的深度更大,则计\(p_v=v\),并回溯\(u\)的祖先\(p_u\),使\(p_u\)满足\(depth(p_u)=depth(p_v)\)。若\(v\)深度更大则同理;
4) 判断\(p_u=p_v\)是否成立,若成立则算法返回\(p_u\);
5) 设置\(p_u = p_u.parent\),\(p_v = p_v.parent\)。回到(4);
朴素算法求1个顶点对的LCA有代价上界\(O(|V|)\),所以求\(n\)对顶点的LCA有代价上界\(O(n\cdot |V|)\)。接下来将讨论Tarjan算法,该算法基于并查集数据结构,其代价为\(O(n+|V|)\)。Tarjan算法是离线算法,也就是说想要Tarjan算法在\(O(n+|V|)\)的代价内求出多个顶点对的LCA,必须一次提供所有的待求LCA的顶点对。而朴素算法是在线算法,“一次性给出多个顶点对,一次性求出多个LCA”和“逐次给出顶点、逐次求出LCA”对于朴素算法而言,其在解决方式上没有任何本质上的区别。
离线算法与在线算法
为了能够讨论LCA问题的离线算法,这里先给出两个概念:
1) 离线算法:指在算法开始前必须确定所有的输入,然后算法执行完毕,给出输出。换句话说,在构造离线算法的时候,不需要考虑“先给算法提供部分输入,算法先基于这部分输入执行,然后再提供部分输入,算法再基于这两部分输入继续执行”等等的情况。一般在寻找解决问题的算法时,默认都是指找问题的离线算法。比如之前讨论的大部分的排序算法、DP算法等,都默认了算法一次性接受了问题的全部输入;
2) 在线算法:与离线算法相反,其允许在算法开始前只接受一部分的输入,并且能够基于这部分输入进行一些有意义的计算。其是按照“输入-计算-输入-计算-输出”的流程工作的,当然也可以中途给出部分的“问题答案”(即计算结果、输出)。比如“输入-计算-输入-计算-输出-输入-计算-输出”这样的流程;
Tarjan离线LCA算法
离线的Tarjan算法的输入是多个顶点对\([(u_1,v_1),(u_2,v_2)…]\)的形式。定义\(s[n]\)表示关于顶点\(n\)的集合,如果输入序列存在元素\((u,n)\)或\((n,u)\)那么就将\(u\)加入到集合\(s[n]\)中。然后可得到未优化的Tarjan算法,这里为了方便描述递归的过程,把下面的算法的步骤用\(F(u)\)表示,其中\(u\)为树节点;
1) 将\(u\)染灰;
2) 遍历\(s[u]\)集合中的所有节点(计为\(v\))
3) 若\(v\)未染色,不做任何操作;
4) 若\(v\)为灰,记录\((u,v)\)的LCA是\(v\);
5) 若\(v\)为黑,从\(v\)向上回溯,直到发现最近的灰节点(计为\(v_p\)),记录\((u,v)\)的LCA是\(v_p\);
6) 对\(u\)的所有子节点(计为\(u_c\))执行\(F(u_c)\);
7) 将\(u\)染黑;
在给定集合\(s\)与树根\(r\)后,执行\(F(r)\)即可得到所有的待求LCA。
算法的正确性比较容易验证,首先是步骤(4)(5)的正确性,根据DFS的性质,在\(u\)的子DFS开始时,图上所有灰节点刚好全部都是\(u\)的祖先或\(u\)本身,那显然距离\(v\)最近的灰色节点。然后是步骤(3)的正确性,由于预先已经得到了集合\(s\),所以在求任意一个顶点对\((u,v)\)的LCA时,整体DFS不是先遍历\(u\)就是先遍历\(v\),如果只考虑先遍历\(v\)的情况那就可以在步骤(3)不进行任何操作,并且不会错过任何一个“问题序列”中的问题。
因为无法确定每次步骤(5)中有几次回溯,该流程的代价达不到\(O(n + |V|)\)。如果想要优化回溯次数,自然想到的是维护一个数据结构,使其在整个DFS过程中维护“当前所有黑节点的最近灰祖先”信息,这样就无需回溯只需从这个数据结构中查询即可。所以接下来的问题是如何构造这样的数据结构呢?
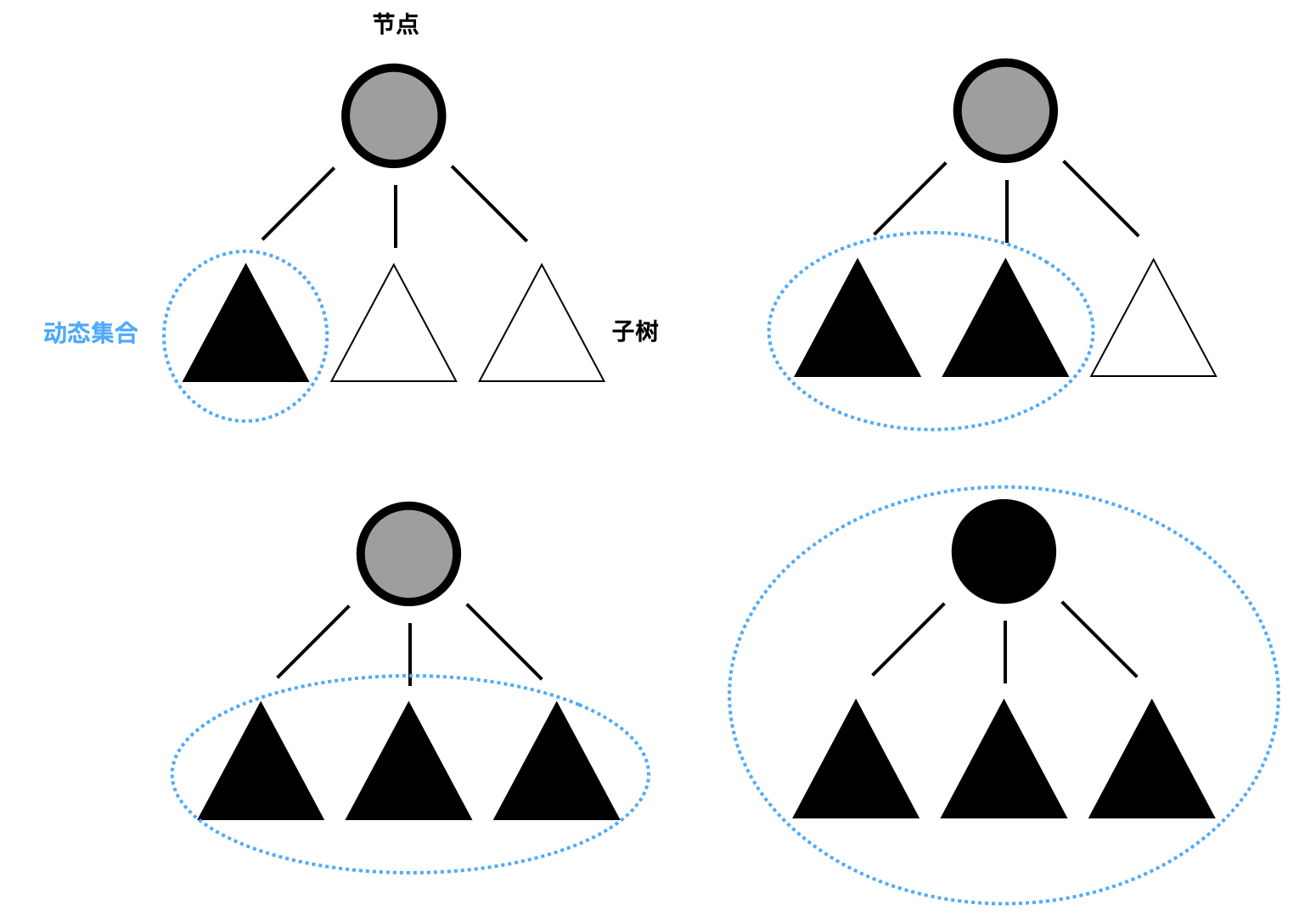
根据DFS的性质可发现在DFS过程中,任意节点\(x\)刚刚染黑(刚刚结束DFS)的时刻,\(x\)的所有代子节点都是黑色的,\(x\)的父节点是灰色的。有由于DFS是“自上而下染灰,再把灰色节点自下而上染黑的”,故在DFS的任意时刻,任意黑节点存在“最远黑祖先(可以是其本身)”。根据DFS性质“最远黑色祖先”有灰色父节点或没有父节点(如果整个DFS已结束“最远黑色祖先”就是树根)。所以说如果能在DFS任意时刻,记录每个黑色节点的“最远黑色祖先”就间接记录了“最近灰色祖先”。
考虑用并查集实现该数据结构,如上图所示,蓝色虚线部分代表了某个动态集合的变化,每个动态集合可能含多个“最远黑色祖先”,但这些“最远黑色祖先”都有相同的灰父节点,也就是说每个动态集合中的节点都有共同“最近灰祖先”。可通过映射记录“动态集合的代表-最近灰色祖先”关系。
下面给出上述流程的“并查集优化版本”,其除了沿用上述\(F(u)\)与\(s\)以外,还需要动态的维护一个并查集\(d\),和一个“动态集合的代表-最近灰色祖先”的映射\(m\)。需要注意的是动态集合的代表有可能会因为\(UNION\)操作而发生变化,所以\(UNION\)结束后要立刻根据情况更新\(m\),具体步骤如下:
1) 将\(u\)染灰,执行\(d.MAKE(u)\);
2) 遍历\(s[u]\)集合中的所有节点(计为\(v\))
3) 若\(v\)未染色,不做任何操作;
4) 若\(v\)为灰,记录\((u,v)\)的LCA是\(v\);
5) 若\(v\)为黑,记录\((u,v)\)的LCA是\(m[d.FIND(v)]\);
6.1) 对第1个子节点\(u_1\)执行\(F(u_1)\),\(m[d.FIND(u_1)] = u\)。
6.2) 对第2个子节点\(u_2\)先后执行\(F(u_2)\),\(d.UNION(u_1,u_2)\),\(m[d.FIND(u_1)] = u\)。
6.3) 对第3个子节点\(u_3\)先后执行\(F(u_3)\),\(d.UNION(u_1,u_3)\),\(m[d.FIND(u_1)] = u\);
7) 将\(u\)染黑,执行\(d.UNION(u_1,u)\);
在给定集合\(s\)、树根\(r\)、空并查集\(d\)、空映射\(m\)后执行\(F(r)\)即可得所有待求LCA(动态集合的合并流程如上图所示)。分析整个算法的时间复杂度,构造集合\(s\)的代价显然是\(n\)。执行\(F(r)\)时,每个子DFS至多附带有限次代价近似为\(O(1)\)的并查集操作。所以\(F(r)\)的代价近似为\(O(|V|)\),总代价近似为\(O(n+|V|)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 | class DisjointSet: def __init__(self): self.p = {} self.rank = {} def make(self, key): assert key not in self.p, '当前key已存在' self.p[key] = key self.rank[key] = 0 def find(self, key): if self.p[key] != key: self.p[key] = self.find(self.p[key]) return self.p[key] def union(self, key1, key2): key1 = self.find(key1) key2 = self.find(key2) if self.rank[key1] > self.rank[key2]: self.p[key2] = key1 else: self.p[key1] = key2 if self.rank[key1] == self.rank[key2]: self.rank[key2] += 1 class TreeNode: def __init__(self, key, children=None): self.key = key self.children = [] if not children else children def lca(root, questions): s = dict() d = DisjointSet() m = dict() color = dict() result = dict() for q in questions: if q[0] not in s: s[q[0]] = set() if q[1] not in s: s[q[1]] = set() s[q[0]].add(q[1]) s[q[1]].add(q[0]) if q[0] not in result: result[q[0]] = {} if q[1] not in result: result[q[1]] = {} dfs(result, root, color, s, d, m) return result def dfs(result, node, color, s, d, m): color[node.key] = 1 d.make(node.key) if node.key in s: for v in s[node.key]: if v not in color: pass elif color[v] == 1: result[node.key][v] = v result[v][node.key] = result[node.key][v] else: result[node.key][v] = m[d.find(v)] result[v][node.key] = result[node.key][v] first_node = None for sn in node.children: if sn.key not in color: dfs(result, sn, color, s, d, m) if not first_node: first_node = sn else: d.union(first_node.key, sn.key) m[d.find(first_node.key)] = node.key if first_node: d.union(first_node.key, node.key) color[node.key] = 2 root = TreeNode('a', [ TreeNode('b', [ TreeNode('e', [ TreeNode('h', [ TreeNode('i') ]) ]), TreeNode('f', [ TreeNode('j', [ TreeNode('l', [ TreeNode('x') ]) ]), TreeNode('k') ]), TreeNode('g') ]), TreeNode('c'), TreeNode('d', [ TreeNode('m', [ TreeNode('n') ]) ]) ]) result = lca(root, [ ('a', 'b'), ('i', 'l'), ('n', 'd'), ('b', 'c'), ('n', 'i'), ('k', 'l'), ('x', 'x'), ('x', 'b'), ('x', 'k') ]) print( result['a']['b'], result['i']['l'], result['n']['d'], result['b']['c'], result['n']['i'], result['k']['l'], result['x']['x'], result['x']['b'], result['x']['k'], ) |