Ford-Fulkerson方法
有流网络\(G=(V,E)\),其容量\(c\)(默认整数)、流\(f\)、源点\(s\)与汇点\(t\)。\(G\)与\(f\)给定\(G_f\)与\(c_f\)。则有步骤:
1) 遍历\((u,v) \in E\),初始化流变量\((u,v).f=0\);
2) 若当前\(G_f\)中存在某个增广路\(p\)则继续迭代,否则停机;
3) 求出增广路容量\(c_f(p)=min\{c_f(u,v)|(u,v) \in p\}\);
4) 遍历\((u,v) \in p\),若\((u,v)\in E\),\((u,v).f+=c_f(p)\),否则\((v,u).f-=c_f(p)\),返回(2);
其之所以不称为算法是因为(2)未有细节,算法与代价无法确定,但可验证其正确性。设每次(2)结束后发现某个\(G_f\)的增广路\(p\),\(f\)更新为\((f\uparrow f_p)\),一定有\(|(f\uparrow f_p)|>|f|\),\(G_f\)与\(c_f\)被\((f\uparrow f_p)\)更新,此时\(p\)一定不是新的\(G_f\)的增广路,回到(2)。循环直到流值达到最大流值,此时(2)无法找到增广路,由最大流最小割定理当前\(f\)即最大流。
Ford-Fulkerson方法满足称为“完整性定理”的性质,即其求得的整数容量流网络的最大流\(f\),不仅\(|f|\)为整数(之前文章有讨论),任意\(f(u,v)\)都为整数,该性质根据上述流程可以比较容易的看出来。
Ford-Fulkerson算法(一般增广路算法)
FF方法的最基本实现,其在流网络数据结构上额外维护残存网络,实现(2)是在当前残存网络\(G_f=(V,E_f)\)的\(s\)上用BFS或DFS发现增广路,由于\(E_f\)被残存容量\(c_f\)(即当前流\(f\))给定,故BFS或DFS途中发现\(t\)即完成对增广路的确定。根据之前文章\(|E_f|\leq 2|E|\)与\(|E|\geq |V|-1\),该步骤有代价上界\(O(|V|+|E_f|)=O(|V|+|E|)=O(|E|)\)。
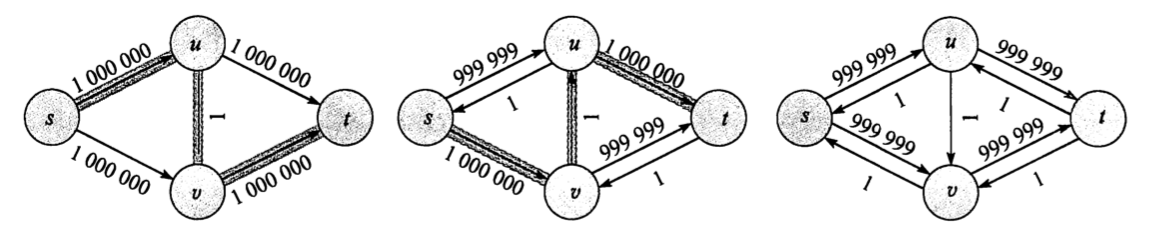
分析算法代价,每次发现增广路有代价上界\(O(|E|)\),转为正整数容量后问题的最大流为\(f^*\),每次发现增广路\(p\)后,\(|f|\)自增到某个正整数(因为\(c_f\)为整数),若认为每次发现增广路\(|f|\)自增1,则外循环有次数上界\(|f^*|\),内循环是遍历当前\(p\)的边,当前\(p\)的边数显然不大于\(|E|\),故总代价有上界\(O((|E|+|E|)|f^*|)=O(|E||f^*|)\),上图给出了这种上界情况,左一是起始情况,每次当前\(p\)都只使当前\(|f|\)自增1,且这种对称结构使每次内循环\(p\)与\(|E|\)的边数同阶。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 | class NetworkFlow: def __init__(self,s,t): self.s = s self.t = t self.c = {} self.f = {} self.cf = {} def add_edge(self,u,v,c): if None==self.c.get(u): self.c[u] = {} self.f[u] = {} self.cf[u] = {} self.c[u][v] = c self.f[u][v] = 0 self.cf[u][v] = c if None==self.c.get(v): self.cf[v] = {} self.cf[v][u] = 0 def has_edge(self,u,v): return self.c.get(u)!=None and self.c[u].get(v)!=None and self.c[u][v] > 0 def residual_has_edge(self,u,v): return self.cf.get(u)!=None and self.cf[u].get(v)!=None and self.cf[u][v] > 0 def dfs(self,u,visited,pi): if None!=self.cf.get(u): for v in self.cf[u].keys(): if v not in visited and self.residual_has_edge(u,v): pi[v] = u if v == self.t: return visited.add(v) self.dfs(v,visited,pi) def dfs_path(self): pi = {} self.dfs(self.s,{self.s},pi) v = self.t path = [] while pi.get(v)!=None : u = pi[v] path.append((u,v)) v = u path.reverse() return path def updata_f(self,path): cp = float('inf') for u,v in path: cp = min(cp,self.cf[u][v]) for u,v in path: if self.has_edge(u,v): self.f[u][v] += cp else: self.f[v][u] -= cp def updata_gf(self): for u in self.cf.keys(): for v in self.cf[u].keys(): if self.has_edge(u,v): self.cf[u][v] = self.c[u][v] - self.f[u][v] elif self.has_edge(v,u): self.cf[u][v] = self.f[v][u] else: self.cf[u][v] = 0 def ford_fulkerson(self): while True: path = self.dfs_path() if not path: break self.updata_f(path) self.updata_gf() def max_flow_value(self): u = self.s val = 0 if self.c.get(u)!=None: for v in self.c[u].keys(): val += self.f[u][v] return val |
Edmonds-Karp算法(最短增广路算法/SAP算法)
FF方法的更优实现,其从\(s\)找增广路的策略为令\(e\in E\)有相同权重1,再求\(s\)的单源最短路,最后利用记录的前驱\(t.\pi\)确定增广路。该方法每次都找“最短”增广路,BFS可在\(O(|V|+|E|)=O(|E|)\)代价解决这种等边权单源最短路问题。表面上看依然只能确定其有\(O(|E||f^*|)\)的上界,实际上该策略能给出\(O(|V||E|^2)\)的上界。下面证明这点:
a) 路径长度递增:对残存网络\(G_f\),每个\(v\in V-\{s,t\}\)每次求出的最短路值\(\delta_f(s,v)\)不递减;
证明思路是反证法,假设\(G\)上的流量从\(f\)递增为\(f’\)是所有流量递增中第1次使1个或1个以上\(v\in V-\{s,t\}\)的最短路值减小的递增,设\(v\)是这些距离减少的顶点中,在递增后\(\delta_{f’}(s,v)\)值最小的某一个,故\(\delta_{f’}(s,v)<\delta_{f}(s,v)\)。设路径\(p=s…u-v\)为残存网络\(G_{f’}\)中从\(s\)到\(v\)的最短路(可能存在\(u=s\)的情况),故有\(\delta_{f’}(s,u)=\delta_{f’}(s,v)-1\)。根据假设\(u\)的距离是不能减少的(否则一开始就会取代\(v\)),所以\(\delta_{f’}(s,u)\geq \delta_{f}(s,u)\)。这使得\((u,v)\)不能属于递增发生前的残存网络\(G_{f}\),否则会导致\(\delta_{f’}(s,v)\geq \delta_{f}(s,v)\),所以只剩下\((u,v)\notin E_f\)但\((u,v)\in E_{f’}\)的情况,这种情况本身又可分为两种情况,一种是\(f(u,v)=c(u,v)\)但\(0\leq f'(u,v) < c(u,v)\),另一种是\(f(v,u)=0\)但\(0<f'(v,u)\leq c(v,u)\)。这两种情况都意味着\(E_f\)存在边\((v,u)\),然后增广路必然经过\((v,u)\),否则增广路既不经过\((v,u)\)也不能经过\((u,v)\)(这条边不存在),那么根据之前对递增流的定义,应保证满足\(f(v,u)=f'(v,u)\),但已经违反了这点。由于该策略找到的增广路为残存网络\(G_f\)中从\(s\)到\(t\)的其中一个最短路,该最短路包含边\((v,u)\),所以有\(\delta_f(s,v)=\delta_f(s,u)-1\leq \delta_{f’}(s,u)-1 = \delta_{f’}(s,v)-2\),引发矛盾,题设中的节点\(v\)并不存在。
b) 流量递增次数上界:流量递增的次数为\(O(VE)\);
增广路容量最小边为关键边,增广路用于递增流量后,关键边不出现在递增后的新残存网络。证\(E\)的每个边至多成为\(O(|V|)\)次关键边,\((u,v)\)首次作为\(G_f\)的增广路的关键边时\(\delta_f(s,v) = \delta_f(s,u)+1\),仅当之后某个\(G_{f’}\)的增广路含\((v,u)\)时(\(\delta_{f’}(s,u)=\delta_{f’}(s,v)+1\)),之后的增广路才会再次出现\((u,v)\)。综上\(\delta_{f’}(s,u)=\delta_{f’}(s,v)+1 \geq \delta_{f}(s,v) + 1= \delta_{f}(s,u)+2\),故每个边成为关键边后若再次成为关键边,其最短路严格递增。增广路作为路径至多含\(O(|V|)\)条边。递增\(O(|V||E|)\)次后,至少出现\(O(|V||E|)\)次关键边,故这之后将无法再有关键边(增广路)。
c) Edmonds-Karp算法的代价为\(O(|V||E|^2)\);
每次递增后还需要BFS利用\(O(|E|)\)时间求得等权重单源最短路。
实现时直接把Ford-Fulkerson算法中的DFS换成BFS即得Edmonds-Karp算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 | from collections import deque class NetworkFlow: def __init__(self,s,t): self.s = s self.t = t self.c = {} self.f = {} self.cf = {} def add_edge(self,u,v,c): if None==self.c.get(u): self.c[u] = {} self.f[u] = {} self.cf[u] = {} self.c[u][v] = c self.f[u][v] = 0 self.cf[u][v] = c if None==self.c.get(v): self.cf[v] = {} self.cf[v][u] = 0 def has_edge(self,u,v): return self.c.get(u)!=None and self.c[u].get(v)!=None and self.c[u][v] > 0 def residual_has_edge(self,u,v): return self.cf.get(u)!=None and self.cf[u].get(v)!=None and self.cf[u][v] > 0 def bfs_path(self): queue = deque([self.s]) visited = set() pi = {} while len(queue)>0: u = queue.popleft() visited.add(u) for v in self.cf[u].keys(): if v not in visited and self.residual_has_edge(u,v): pi[v] = u if v == self.t: path = [] while pi.get(v)!=None : u = pi[v] path.append((u,v)) v = u path.reverse() return path queue.append(v) def updata_f(self,path): cp = float('inf') for u,v in path: cp = min(cp,self.cf[u][v]) for u,v in path: if self.has_edge(u,v): self.f[u][v] += cp else: self.f[v][u] -= cp def updata_gf(self): for u in self.cf.keys(): for v in self.cf[u].keys(): if self.has_edge(u,v): self.cf[u][v] = self.c[u][v] - self.f[u][v] elif self.has_edge(v,u): self.cf[u][v] = self.f[v][u] else: self.cf[u][v] = 0 def edmonds_karp(self): while True: path = self.bfs_path() if not path: break self.updata_f(path) self.updata_gf() def max_flow_value(self): u = self.s val = 0 for v in self.c[u].keys(): val += self.f[u][v] return val |
Dinic方法
FF方法是在残存网络不断找增广路,Dinic方法在残存网络不断建立层次图并在层次图不断找增广路。Dinic方法可被“归约”进FF方法,所以有时也认为Dinic方法是FF方法的“实现”。下面定义Dinic方法中最重要的层次图。
层次图:设\(G_f\)中\(v.\pi\)为\(s\)到\(v\)的最短路值(边权为1),\(G_f\)的层次图\(G’_f\)的边集为\(\{ (u,v) \in E_f | v.\pi = u.\pi + 1 \}\),顶点集为边的顶点。可想象将层次图“叠加”于残存网络,二者随增广路更新“动态变化”,这可把问题直观化。
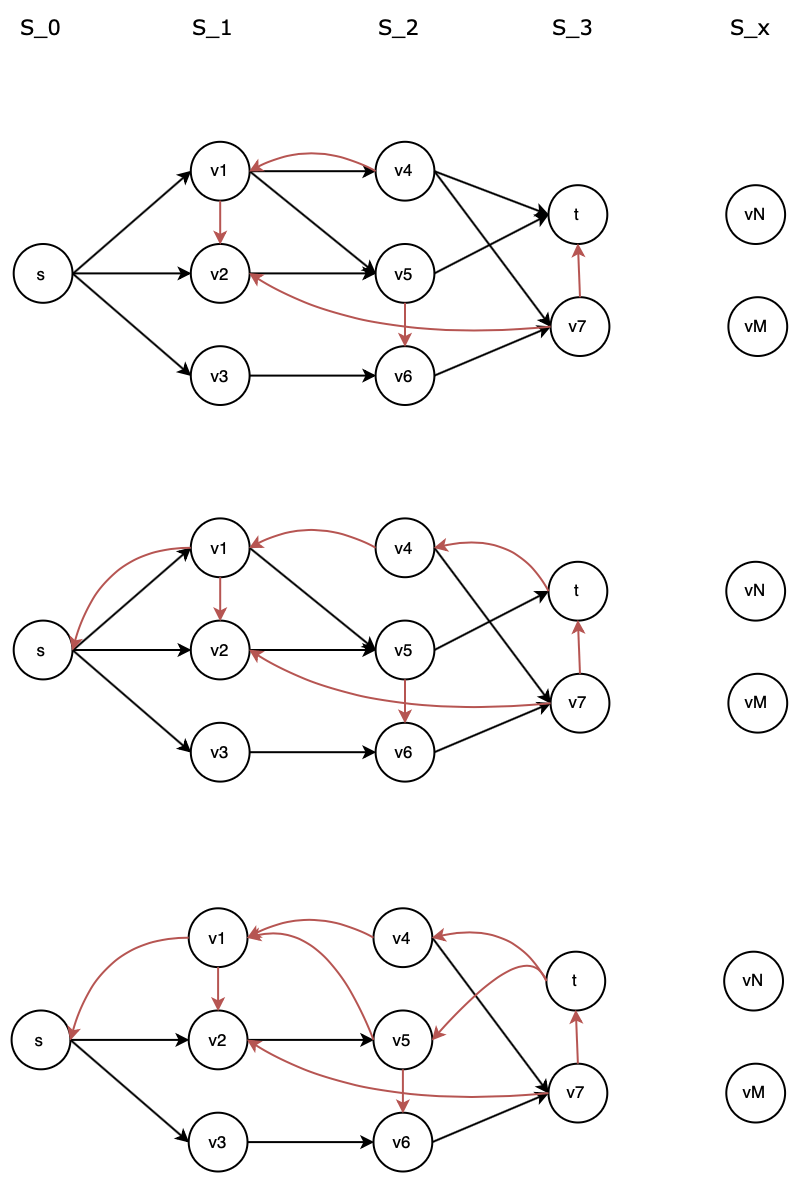
把层次图顶点划入集合\(S_0,S_1,…\),其中\(S_i\)为\(G_f\)上距离\(s\)最短路值为\(i\)的所有顶点。利用该集合可将\(G_f\)重新“画”成分层的图(如上图)。其中黑边为\(G_f\)同属于\(G’_f\)的边,红边为\(G_f\)的其他边。给出边的相关性质:
1) 不同\(S_i\)间无重复元素,\(i\)是从0开始递增的连续整数,其值有上界\(|V|-1\);
2) \(G_f\)仅包含黑边红边,黑边从\(S_i\)达\(S_{i+1}\),红边从\(S_i\)达\(S_j(j\leq i)\);
\(G_f\)存在\(S_i\)到\(S_j(j\geq i+2)\)的边与\(G’_f\)定义矛盾。\(S_i\)到\(S_j(j=i+1)\)的边符合\(G’_f\)定义,\(S_i\)到\(S_j(j\leq i)\)的边不符合\(G’_f\)定义但可存在于\(G_f\)。
3) 若\(G’_f\)中存在从\(u\)到达\(v\)的路径,那么所有不同路径的长度相等;
否则会导致同个顶点有不同的两个最短路值(\(\pi\))的矛盾。
4) 若\(G’_f\)与\(G_f\)中都存在从\(u\)到达\(v\)的路径,则\(G’_f\)中的路径的长度最短;
由于所有黑边路径都按\(S_i,S_{i+2},S_{i+3}…\)推进,那么只要其中存在一条红边就会被“拉回”一次,然后再被黑边“推进”,只会比黑边路径长。
Dinic方法的思路很大程度依赖于上述的“分层图像”,这里给出“无具体实现”的Dinic方法的流程:
1) 利用\(G\)与\(f\)建立残存网络\(G_f\),利用\(G_f\)建立层次图\(G’_f\);
2) 在\(G’_f\)上第0次找增广路,若找到增广路\(p\),用\(p\)更新\(f\)与\(G_f\),但不重新建立\(G’_f\),而是从\(G’_g\)删除原\(p\)失去的边。若未找到增广路则当前的\(f\)为最大流,算法退出;
3) 在\(G’_f\)上第1次找增广路,若找到增广路\(p\),用\(p\)更新\(f\)与\(G_f\),但不重新建立\(G’_f\),而是从\(G’_g\)删除原\(p\)失去的边。若未找到增广路则去步骤(1)重建层次图……..在\(G’_f\)上第i次找增广路,若找到增广路\(p\),用\(p\)更新\(f\)与\(G_f\),但不重新建立\(G’_f\),而是从\(G’_g\)删除原\(p\)失去的边。若未找到增广路则去步骤(1)重建层次图;
a) 对于步骤(1)刚刚新建的\(G_f\)与\(G’_f\),\(G_f\)存在增广路的充要条件为\(G’_f\)存在增广路。
b) 步骤(3)每次循环时若可从当前\(G’_f\)找到增广路,则其长度与在相应步骤(2)找到的增广路长度\(k\)相等。
\(G’_f\)在任意次删边后都是最初未删边时的子图,若其存在长度不等于\(k\)的增广路会破坏未删边时的\(G’_f\)的定义(最短路性质)。
c) 步骤(3)每次循环时若可从当前\(G’_f\)找到增广路\(p\),则可从当前\(G_f\)中找到\(p\)。否则当前\(G_f\)无增广路或仅有长度大于\(k\)的增广路。
步骤(3)在每次循环中更新\(G_f\)只会使其发生两类变化,第一类是\(G_f\)至少失去一条原\(p\)上的边,第二类是\(G_f\)上会加入若干原\(p\)上的边的反向边。从上述集合与分层图像的角度看来,\(G_f\)至少失去一条\(S_i\)到\(S_{i+1}\)的边,增加若干\(S_{i+1}\)到\(S_i\)的边,这里\(0\leq i \leq k-1\)。
对于第一种情况,步骤(3)在每次循环利用增广路\(p\)更新\(G_f\)只会使其有两类变化,一类是\(G_f\)至少失去一条原\(p\)上的边,二类是\(G_f\)上会加入若干原\(p\)上的边的反向边。从上述集合与分层图像的角度看来,\(G_f\)至少失去一条\(S_i\)到\(S_{i+1}\)的边,增加若干\(S_{i+1}\)到\(S_i\)的边,这里\(0\leq i \leq k-1\)。\(G_f\)更新后的新增边与\(G’_f\)无关,消失边在\(G’_f\)中也被删除。故每次“更新\(G_f\)删边\(G’_f\)”后,\(G’_f\)都为\(G_f\)的子图,\(G’_f\)的路径必为\(G_f\)的路径。
对于第二种情况,无论哪次到达步骤(3)的哪次循环,\(G_f\)与\(G’_f\)都经历了步骤(1)的“初始化”与(2)的至少1次的“更新删边”,并确定了\(G’_f\)上的增广路长度\(k\)。若当前\(G_f\)存在增广路\(p\),从分层图像视角看来,\(p\)不存在\(S_i\)到\(S_j(j\geq i+2)\)的边,因为在\(G_f\)与\(G’_f\)刚被建立时,存在这样的边将违反\(S_i\)的定义,且之后无论如何更新\(G_f\)都只能在\(S_i\)与\(S_j(j=i+1)\)这样的集合对中加边或减边。故\(p\)只能存在\(S_i\)到\(S_j(j\leq i+1)\)的边,这显然使得\(p\)的长度无法小于\(k\)。若\(p\)的长度等于\(k\),那么其仅存在\(S_i\)到\(S_j(j=i+1)\)的边,即\(S_0,S_1…S_k\),这条路径由于与\(G’_f\)刚初始化后找到的第一个增广路的长度\(k\)相同,根据\(G’_f\)的定义,其一定也存在于刚初始化时的\(G’_f\)上。此时\(p\)存在于当前\(G_f\)上,由于每次更新都无法新增\(S_i\)到\(S_{i+1}\)的边,故之前从未使\(G_f\)删除过\(p\)上的边,因而也就从未在\(G’_f\)删除过\(p\)上的边,这与\(G’_f\)上无法找到\(p\)矛盾,说明\(p\)的长度不能等于\(k\)。当增广路长度大于\(k\)时则不排除可能存在\(…S_i,S_i,S_{i+1}..\)或\(…S_i,S_{i+1},S_i..\)等形式的增广路。
该流程虽未指明每次如何在\(G’_f\)找增广路,但可以简单讨论其正确性与某些部分的代价上界:
d) 算法中的步骤(1)至多被到达\(O(|V|)\)次。
最坏情况首次到达增广路长度为1,之后每次到达长度+1。由于增广路是路径故其至多有\(|V|-1\)条边,这样就得到上界\(O(|V|)\)。
e) 可以将Dinic方法归约为Ford-Fulkerson方法,这说明Dinic算法是正确的。
利用上述(a)(c)可把流程转化为完全是关于残存网络\(G_f\)的:每次(2)中是否找到增广路则等价于\(G_f\)是否有增广路,步骤(3)等价于“重复找\(G_f\)长度与\(p\)相同的增广路”。这样Dinic方法等价于“若在\(G_f\)找到1个或更多长度相同的增广路,则依次用于更新\(G_f\),然后继续寻找…直到无法找到1个增广路”,而一般的FF方法是“若在\(G_f\)找到1个增广路,则用于更新\(G_f\),然后继续寻找…直到无法找到1个增广路”。所以Dinic方法可以看作是为FF方法提供了更具体的“找增广路-更新残存网络”的流程,这也说明了Dinic方法的正确性。
Dinic算法(连续最短增广路算法)

不同于CLRS的白灰黑DFS,也不同于白灰DFS,接下来的DFS是“不染色”的,无论何时每个顶点都是白色,即每个顶点的子DFS都要对所有出边直达的顶点执行子DFS。下面讨论从层次图源点DFS得到的生成树的性质:
a) 第\(i\)层的节点来自\(S_i\);
b) 同层可能出现重复节点,重复节点的子树相同;
c) 树边包含所有层次图的边;
d) 从\(s\)执行的DFS,DFS树的生成次序等于DFS树前序遍历的次序;
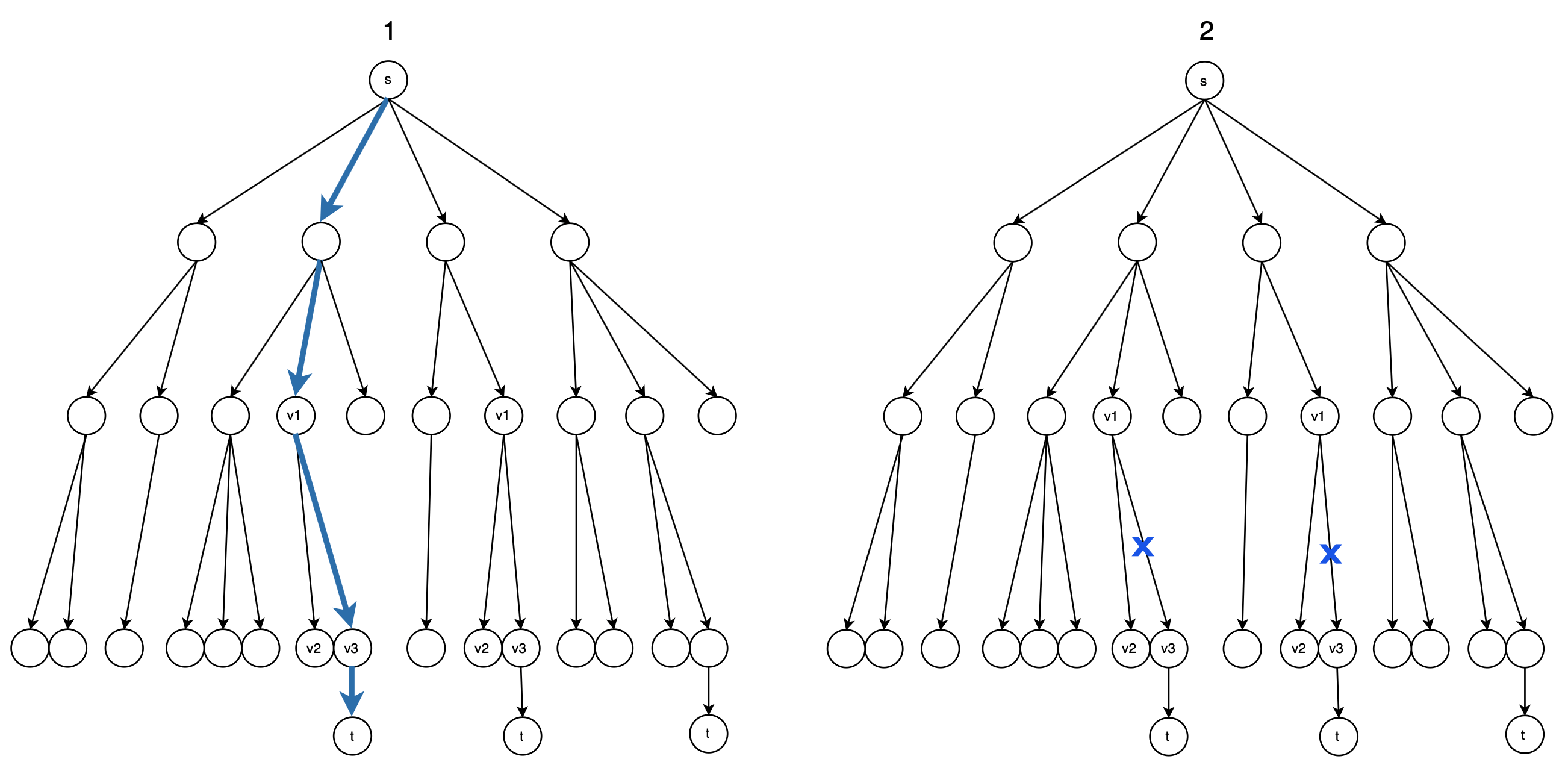
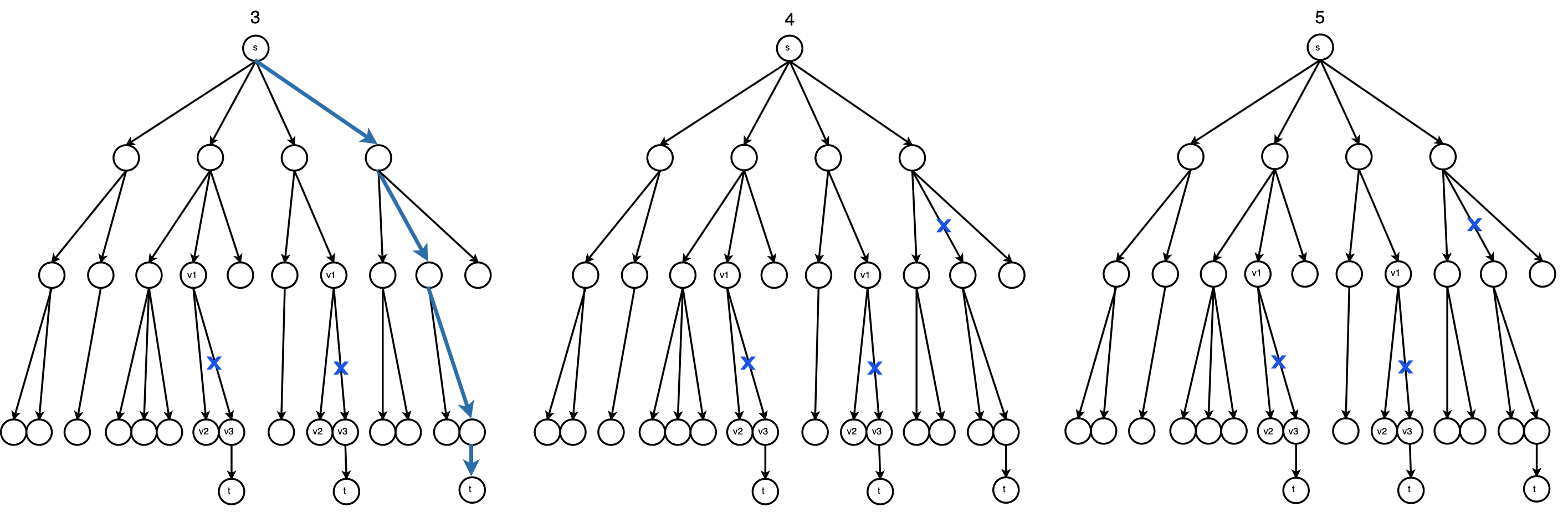
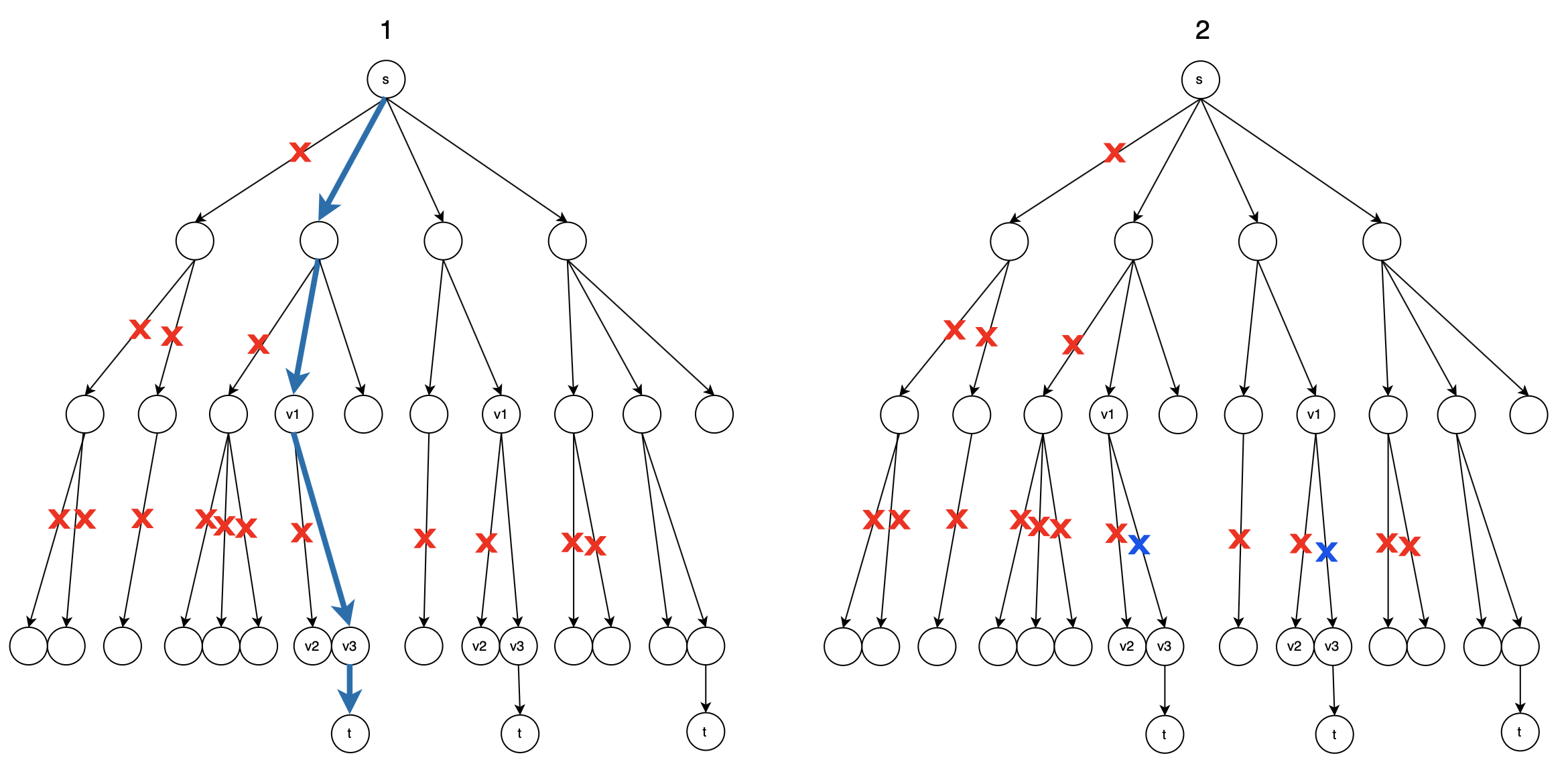
对上述Dinic方法步骤(2)(3)的最简单实现是“从\(G’_f\)的\(s\)开始DFS,发现增广路,更新\(G_f\)删边\(G’_f\),然后从\(G’_f\)的\(s\)开始全新的DFS…直到某次DFS无增广路”,其DFS树的变化如上图第一张。这种实现的代价很大,但是其每次能否DFS到增广路完全等价于Dinic方法中的“能否找到增广路”,故其正确性是显然的,但代价太大。下面给出另一种实现,如果能证明这种实现每次所找到的增广路与上一种实现相同,那么就能证明这种实现是正确的:
1) 从未删边的\(G’_f\)的\(s\)执行DFS;
2) 若子DFS发现当前顶点\(v\neq t\)且没有出边,则回溯的将\(G’_f\)中父DFS到达\(v\)的边\((u,v)\)删除;
3) 若子DFS发现当前顶点\(v=t\),利用该增广路更新\(G_f\)与删边\(G’_f\),并从\(s\)开始新的DFS;
4) 直到最终某次DFS没有发现增广路,算法结束;
上图第一张是第一种实现,每次发现增广路并更新后的DFS生成树与其变化(蓝色叉表示用增广路更新后失去的边)。由于所有图边都在DFS树上,并且多个树边可能对应于同个图边,故删除1条图边可能导致删除多个树边。由于这种DFS的不染色特性,删除图边除了需要删除对应树边外,新的DFS树的结构是不会有变化的,对于染色DFS如果删除图边可能导致DFS树中的某个节点出现在新DFS树的其他子树上。
上图第二张是第二种实现,DFS回溯时删的边用红叉表示,这样删边同样是不会影响DFS树的“骨架”,但是这会导致删除后续DFS将到达的边。被本轮DFS删去的边不可能是本轮或之后的DFS中的增广路的边,否则被删去的边的子DFS必然会发现增广路。这两种实现的DFS次序是相同的,只不过后者将会“剪掉”没有用的边。
分析第二种实现的代价,根据层次图与该DFS性质,在所有DFS轮次中,红叉边仅到达\(O(1)\)次,增广路长度有上界\(O(|V|)\),故增广路更新流量失边的最坏情况为每达\(O(|V|)\)次边仅失1条边。综上每到达\(O(|V|)\)条边至少失去1条边,最坏情况是若到达\(O(|V||E|)\)次边,则失去全部图边。结合层次图建图次数上界有总代价\(O(|E||V|^2)\)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 | from collections import deque class NetworkFlow: def __init__(self,s,t): self.s = s self.t = t self.c = {} self.f = {} def add_edge(self,u,v,c): if None == self.c.get(u): self.c[u] = {} self.f[u] = {} self.c[u][v] = c self.f[u][v] = 0 def get_cap(self,u,v): return self.c[u][v] if u in self.c and v in self.c[u] else 0 def get_residual_cap(self,u,v): if u in self.c and v in self.c[u] and self.c[u][v]>0: return self.c[u][v] - self.f[u][v] if v in self.c and u in self.c[v] and self.c[v][u]>0: return self.f[v][u] return 0 def make_residual_edges(self): edges = {} for u in self.c.keys(): for v in self.c[u].keys(): x = self.get_residual_cap(u,v) if x > 0: if u not in edges: edges[u] = {} edges[u][v] = x x = self.get_residual_cap(v,u) if x > 0: if v not in edges: edges[v] = {} edges[v][u] = x return edges def make_level_edges(self): res = self.make_residual_edges() q = deque([self.s]) vis = {self.s} level = {} while len(q)>0: u = q.popleft() if u in res: for v in res[u].keys(): if not v in vis: if u not in level: level[u] = set() level[u].add(v) vis.add(v) q.append(v) return level def dfs_level(self,level,u,path): path.append(u) if u == self.t: return True if u in level: for v in list(level[u]): if self.dfs_level(level,v,path): return True level[u].remove(v) path.pop() return False def update_flow_level(self,path,level): pf = float('inf') for i in range(len(path)-1): u,v = path[i],path[i+1] pf = min( pf, self.get_residual_cap(u,v) ) for i in range(len(path)-1): u,v = path[i],path[i+1] if self.get_cap(u,v) > 0: self.f[u][v] += pf else: self.f[v][u] -= pf if self.get_residual_cap(u,v) == 0: level[u].remove(v) def dinic(self): while True: j = 0 level = self.make_level_edges() while True: path = [] if self.dfs_level(level,self.s,path): self.update_flow_level(path,level) j += 1 else: break if j == 0: break def max_flow_value(self): u = self.s val = 0 for v in self.c[u].keys(): val += self.f[u][v] return val |