流网络
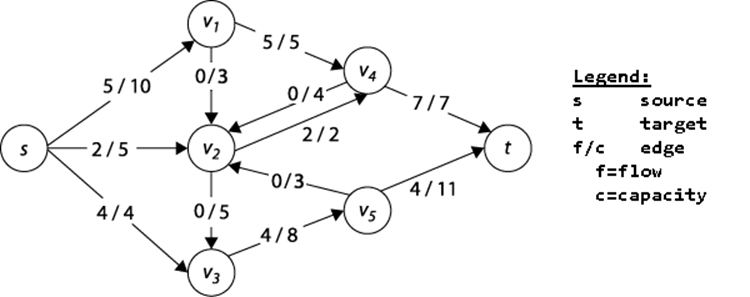
1) 流网络是附加了条件的带权重(容量)的有向图\(G=(V,E)\),其附加条件与附加定义如下:
源与汇:给定\(G\)的同时需给定源\(s\)与汇\(t\)两个特殊顶点;
边与容量:给定\(G\)的边\((u,v)\)的同时需给定边容量\(c(u,v) > 0\),并且边集必须满足:
i. 不允许反向边(若\((u,v)\in E\)则\((v,u)\notin E\));
ii. \(s\)仅有入边且\(t\)仅有出边;
iii. 任意\(v \in V-\{s,t\}\)从\(s\)可达\(v\)且从\(v\)可达\(t\);
iv. 除\(s\)以外每个顶点至少有一条入边故\(|E| \geq |V| – 1\);
2) 流是函数\(\{ f(u,v) | (u,v)\in E \}\),流可定义于流网络与残存网络。其附加条件与附加定义如下:
值:定义\(|f|=\sum_{v\in V}f(s,v) ~- \sum_{v\in V}f(v,s) \),源的流出减流入(流入用于兼容残存网络);
流量限制:流若满足下述\(G\)给定的限制条件,则称为\(G\)的可行流,流网络通常有多个可行流:
i. \(0 \leq f(u,v) \leq c(u,v)\) (流量上限/容量上限条件);
ii. \(\sum_{v\in V}f(v,u) = \sum_{v\in V}f(u,v) \) (流量守恒条件);
最大流:设\(f\)为流网络的最大流,则对于该流网络的任意其他流\(f’\),有\(|f|\geq |f’|\);
直观上流网络是承载流的“框架”,不同的流会有不同的“总流入量”,人们通常关心怎么在“框架”的限制下,让“总流入量”最大化。最大流在现实中的应用非常广泛,因为其代表着“如何管理有‘流动’属性的资源,能使总效益最大”。目前只是定义了概念与问题,接下来需要进一步定义流网络与其上的一个流所给定的残存网络这样的概念。
* 在接下来的相关证明中,函数如果取到定义域(比如不存在的边)外的自变量,在无特殊约定(忘记约定)时默认函数值等于0。
流网络的残存网络
给定流网络\(G=(V,E)\)(包括容量\(c\))与其上的一个流\(f\),那么就给定了残存网络\(G_f(V,E_f)\)。
1) 源与汇:与给定该残存网络的流网络的源与汇相同;
2) 容量:若\((u,v) \in E\)则\(c_f(u,v)=c(u,v)-f(u,v)\)且\(c_f(v,u)=f(u,v)\),其他情况等于0;
3) 边集:用\(c_f\)定义\(E_f = \{ (u,v) | c_f(u,v)>0 \}\)。\(E_f\)的边是\(E\)的边或反边,故\(|E_f|\leq 2|E|\);
4) 流:根据上述对流的定义,\(G_f\)具有容量、源与汇,故\(G_f\)上同样可定义流\(f’\);
可以发现残存网络允许反向边,每条网络流的边与“边流”对应残存网络至多两条边。在残存容量\(c_f\)限制下,可发现\(G_f\)的流\(f’\)有特殊意义,即对给定的\(G\)的流\(f\)中的任意一条\(f(u,v)\),\(G_f\)与\(c_f\)允许其上存在两条\(f'(u,v)\)与\(f'(v,u)\),这两条残存流可以把\(f(u,v)\)带来的流量“完全退回”或“加满”到\(c(u,v)\),即可以把\(f(u,v)\)带来的流量调整为\([0,c(u,v)]\)间的任意值。这说明如果\(G_f\)上有可行流\(|f’|>0\),那么把\(G_f\)直观的“重叠”到\(G\)上,然后把冗余的“流量出入边”相抵合并可得到\(G\)的新流\(f\uparrow\),那么\(f\uparrow\)的“流边”与\(f\)完全相同(流量不同),不会产生反向边。并且其显然符合流量上限,以及流量守恒(互相抵消)。更重要的是\(f\uparrow\)保留了\(f’\)所带来的\(s\)的新的流入。这个重要结论需要被形式化的表述为引理:
设\(f’\)为\(G_f\)的任意可行流,定义函数\((f\uparrow f’)(u,v)=f(u,v)+f'(u,v)-f'(v,u)\)当\((u,v)\in E\)时,其他情况时\((f\uparrow f’)=0\)。则\((f\uparrow f’)\)是\(G\)的可行流,并且其值\(|(f\uparrow f’)|=|f|+|f’|\)。
证\((f\uparrow f’)\)符合容量上限,求解关于\((f\uparrow f’)(u,v)\)的不等式如下:
\((f\uparrow f’)(u,v) = f(u,v)+f'(u,v)-f'(v,u)\geq f(u,v)+f'(u,v)-f(u,v) = f'(u,v) \geq 0\)
\((f\uparrow f’)(u,v)\leq f(u,v)+f'(u,v) \leq f(u,v)+c_f(u,v)=f(u,v)+c(u,v)-f(u,v)=c(u,v)\)
证\((f\uparrow f’)\)流量守恒,设\(u \in V-\{s,t\}\),对\(u,v\)求和有等式:
\(\sum_{v\in V}(f\uparrow f’)(u,v) = \sum_{v\in V}(f(u,v)+f'(u,v)-f'(v,u))\)
\(= \sum_{v\in V}f(u,v)+ \sum_{v\in V}f'(u,v)- \sum_{v\in V}f'(v,u) \)
\(= \sum_{v\in V}f(v,u)+ \sum_{v\in V}f'(v,u)- \sum_{v\in V}f'(u,v) \) (\(f\)与\(f’\)为流,故\(f\)与\(f’\)对同个\(V\)流量守恒)
\(= \sum_{v\in V}(f\uparrow f’)(v,u) \)
证\(|f\uparrow f’| = |f| + |f’|\),设\(V_1=\{v|(s,v) \in E\}\)与\(V_2=\{v|(v,s) \in E\}\)。则\(V_1\bigcap V_2\)为空(无反向边):
\(|(f\uparrow f’)|= \sum_{v\in V}(f\uparrow f’)(s,v) ~-~ \sum_{v\in V}(f\uparrow f’)(v,s) \)
\(= \sum_{v\in V_1}(f\uparrow f’)(s,v) ~-~ \sum_{v\in V_2}(f\uparrow f’)(v,s) \)
\(= \sum_{v\in V_1}(f(s,v)+f'(s,v)-f'(v,s)) ~-~ \sum_{v\in V_2}(f(v,s)+f'(v,s)-f'(s,v)) \)
\(= \sum_{v\in V_1}f(s,v) ~- \sum_{v\in V_2}f(v,s) + \sum_{v\in V_1\bigcup V_2}f'(s,v) ~- \sum_{v\in V_1\bigcup V_2}f'(v,s) \)
\(= \sum_{v\in V}f(s,v) ~- \sum_{v\in V}f(v,s) + \sum_{v\in V}f'(s,v) ~- \sum_{v\in V}f'(v,s) = |f| + |f’| \)
最后一步的后两项\(G_f\)对\(V_1\bigcup V_2\)成立即对\(V\)成立,因为\(G_f\)相比\(G\)至多有反向边,没有其他情况的边。
对原流网络与原流给定的残存网络,残存网络的任意流都可以“递增”原网络的流。但这对于解决最大流问题而言,颗粒度仍然太大,如何快速有效的找一个流来“递增”原流仍是未知。故需利用残存网络的增广路的概念,用增广路定义一个残存网络的流用于“递增”,并利用增广路判断是否为最大流。算法实现这两点的代价相对较低。
残存网络的增广路
增广路是残存网络\(G_f\)中从\(s\)到达\(t\)的简单路径\(p\)(即\(p\)的边都有\(c_f>0\));
1) 流:任意\(p\)都可定义流\(f_p(u,v)= min\{ c_f(u,v) | (u,v) \in p \}\)(其他情况为0),其显然是可行的;
2) 递增流:\(|(f\uparrow f_p)|=|f|+|f_p|>|f|\),即利用\(f_p\)可得原流网络的“更大流”;
然后需建立增广路与最大流间的联系,这需要先给出切割与最大流最小割定理这两个概念。
流网络的切割
将流网络\(G=(V,E)\)的\(V\)划分到两个集合\(S\)与\(T=V-S\)中,若满足\(s\in S\)与\(t\in T\),则称\((S,T)\)给定了流网络\(G\)的一个切割,也可称为给定了图\(G\)的切割,因为切割本身不是利用流网络定义的;
1) 净流量:从\(S\)流入\(T\)的净流量\(f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)-\sum_{u\in S}\sum_{v\in T}f(v,u)\);
2) 容量:容量\(c(S,T)=\sum_{u\in S}\sum_{v\in T}c(u,v)\),即可从\(S\)流入\(T\)的最大流量上限;
下面给出图论的最大流最小割定理组,其在不同场景(数学/运筹学/算法)有不同的拆分方式,其可将上文的概念统一。
最大流与最小割
i) 流网络的任意切割\((S,T)\),任意流\(f\),\(f(S,T)=|f|\)恒成立;
该引理是直观的,形式化的证明一下,对\(u\in V-\{s,t\}\)由流量守恒\(\sum_{u\in S-\{s\}}( \sum_{v\in V}f(u,v) – \sum_{v\in V}f(v,u)) = 0\)
加入上式到\(|f|\)定义有\(|f|= (\sum_{v\in V}f(s,v)-\sum_{v\in V}f(v,s))+\sum_{u\in S-\{s\}}( \sum_{v\in V}f(u,v) – \sum_{v\in V}f(v,u)) \)
\(= \sum_{v\in V}(f(s,v)+\sum_{u\in S-\{s\}}f(u,v)) – \sum_{v\in V}(f(v,s)+\sum_{u\in S-\{s\}}f(v,u))\)
\(= \sum_{v\in V}\sum_{u\in S}f(u,v) – \sum_{v\in V}\sum_{u\in S}f(v,u)\)
\(= (\sum_{v\in S}\sum_{u\in S}f(u,v) – \sum_{v\in S}\sum_{u\in S}f(v,u)) + (\sum_{v\in T}\sum_{u\in S}f(u,v) – \sum_{v\in T}\sum_{u\in S}f(v,u))\)
\(= \sum_{v\in T}\sum_{u\in S}f(u,v) – \sum_{v\in T}\sum_{u\in S}f(v,u) = f(S,T)\)
ii) 流网络的任意切割\((S,T)\),任意流\(f\),\(c(S,T)\geq |f|\)恒成立;
iii) 下面的三条是等价的:
1) \(f\)是\(G\)的最大流;
2) \(G_f\)不含增广路(增广路定理);
3) 存在\((S,T)\)使\(|f|=c(S,T)\);
1->2:通过反证法与\(|(f\uparrow f_p)|=|f|+|f_p|>|f|\)立即得证。
2->3:定义\(S=\{v | s或在G_f中从s可达v \}\),\(T=V-S\)。\(G_f\)不含增广路径,故\((S,T)\)为切割。考虑任意的节点对\(u\in S\)与\(v\in T\),若\((u,v)\in E\)则\(f(u,v)=c(u,v)\),否则根据定义有\(c_f(u,v)>0\)即\((u,v)\in E_f\),这将导致\(v\in S\)的矛盾。若\((v,u)\in E\)则\(f(v,u)=0\),否则有\(c_f(v,u)>0\),导致同样矛盾。其他情况\(c(u,v)=c(v,u)=0\),\(f(u,v)=f(v,u)=0\)。结合上述三种情况、切割容量定义、引理(i)有:
\(|f|=f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)-\sum_{u\in S}\sum_{v\in T}f(v,u)=\sum_{u\in S}\sum_{v\in T}c(u,v)-0 = c(S,T)\)
3->1:根据引理(ii)净流量\(f(S,T)\)有上界\(f(S,T)\leq c(S,T)\),故\(|f|=f(S,T)\)只能是最大流。
iv) 最大流的值等于最小割的容量;
流与最大流的线形特征
1) 容量函数值都为整数,则最大流的值为整数;
利用最大流的值等于最小割的容量等于流网络的一部分边的容量和即可。
2) 容量函数为\(c\)最大流值为\(|f|\),设\(k>0\)若令容量为\(kc\)则最大流值为\(k|f|\);
利用最大流的值等于最小割的容量等于流网络的一部分边的容量和,然后可以把\(k\)提到外面。
3) 容量函数\(c\)的值都为正有理数,则存在正整数\(k\)使得\(kc\)的值都为正整数;
利用有理数公理与分母的公倍数即可
通常默认最大流算法输入的边容量是有限小数(有理数),此时问题可化为边容量都为整数的问题,故又可默认输入的边容量都为整数。当容量不都为有理数则不一定可化为整数问题,如容量\([e,\pi,3^{0.5}]\)不可,\([\pi,1.2\pi,1.3\pi]\)可。
最大流中的特殊处理
给出求最大流的例子如下:“设城市A有一家工厂(源节点),其每天都要运送货物到城市B的仓库(汇点),这段路中可以途径许多其他城市(其他的图顶点),由于交通等原因每天能从城市u运到城市v的货物有上限(容量函数\(c(u,v)\)),现在问工厂应该怎么规划运输方案,能使工厂每天运出最大数目的货物(使仓库每天收到最大数目的货物)?”。然后通过这个例子说明在把实际问题建模为求解最大流问题时,将遇到的几种需特殊处理的情况:
1) 反向边:流网络不允许反向边,但在对实际问题建模时会很自然的有反向边。通过上例给出两种处理方法:
i. 构造不影响原问题的新流网络,其中无反向边,方法是在反向边的“中途”插入新顶点,如\((u,v)\)与\((v,u)\)这对边,删除\((u,v)\),加入节点\(k\),加入边\((u,k)\)与\((k,v)\),令\(c(u,k)=c(k,v)=c(u,v)\)。其正确性容易验证;
ii. 将原流网络的一对反向边容量相抵,只留一条抵消过容量的边。这样处理大多不影响原问题,设上例中求解出的最大流\(f\)中有\(f(u,v)>0\)与\(f(v,u)>0\),那显然没必要把部分货物从\(u\)送到\(v\)再送回\(u\);
2) 多源多汇:如果在多个城市有分厂和分仓库,求所有分厂每天可发出的最大货物数量和,有源序列\([s_1…s_i…]\)和汇序列\([t_1…t_j…]\)不符合流网络定义。解决方法同样是构造其他流网络,在原流网络加入超级源\(s\)与超级汇\(t\),加入出边\((s,s_i)\)与入边\((t_j,t)\),把新边容量设为\(\infty\),求解新的流网络。该方法的正确性同样容易验证;