差分约束问题的单源最短路解法

线性规划与差分约束

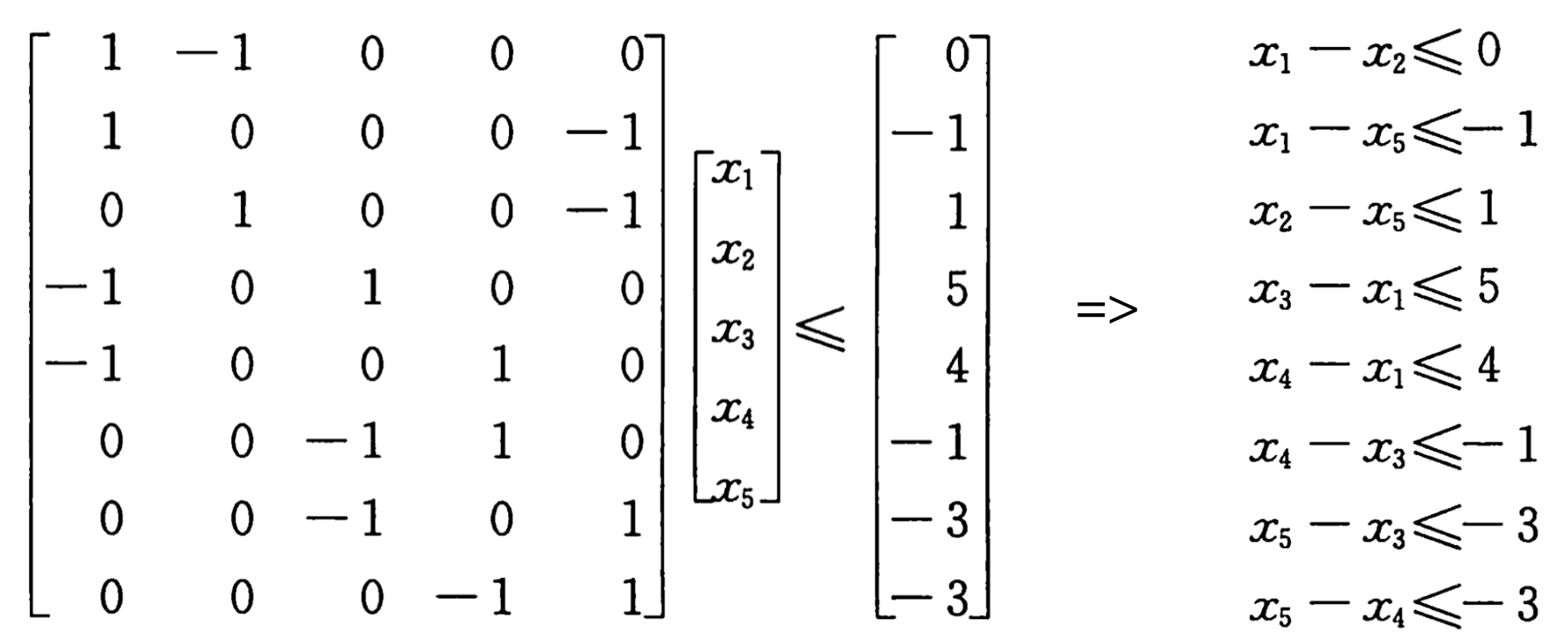
一般形式的线性规划问题可用矩阵来表述，而差分约束为线性规划的特例，其可用有向图表示。给出相关定义：

1) 线性规划：给定\(m\times n\)矩阵\(A\)、\(m\)维向量\(b\)、\(n\)维向量\(c\)。求在\(Ax \leq b\)约束下使\(\sum  c_ix_i\)取最大值的\(n\)维向量\(x\)；

2) 差分约束：若矩阵\(A\)每行是仅有1个-1、仅有1个1、其余都为0的，且\(x\)仅需满足\(Ax \leq b\)约束即可；

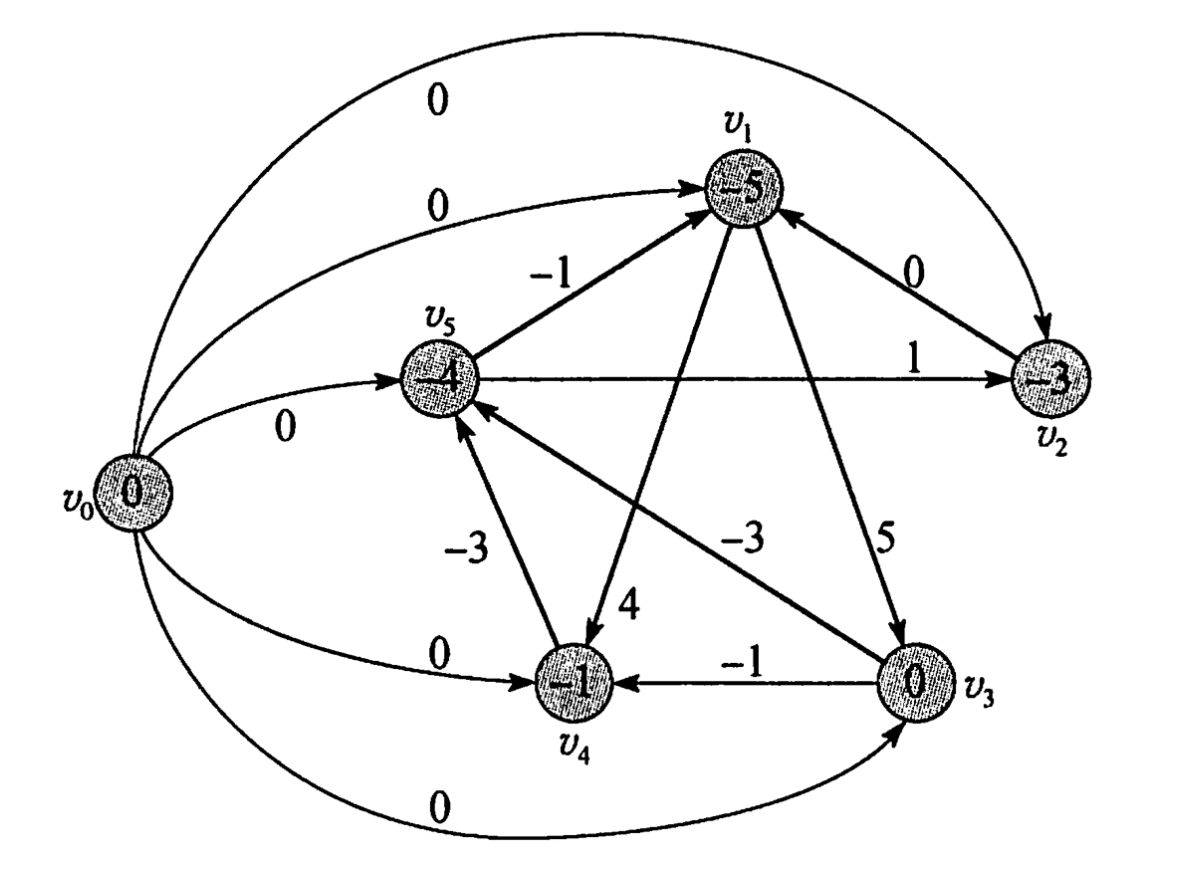
3) 差分约束图：用有向图\(G\)的边\((v_i,v_j)\)与权重\(w(v_i,v_j)\)表示\(x_j – x_i \leq w(v_i,v_j)\)，则\(G\)可表示给定差分约束，再在\(G\)加入\(v_0\)顶点得到\(G’\)，规定\(v_0\)仅有直达其他所有顶点的0权重边。\(G’\)为差分约束图，\(G’\)与\(G\)的解等价；

证明：\(G’\)比\(G\)多\(|V_G|\)个约束，其中的第\(i\)个为\(x_i – x_0 \leq 0\)。\(G’\)的解\(x’=(x’_0,x’_1,…)\)若存在则\((x’_1,…)\)显然为\(G\)的解。\(G\)的解\(x=(x_1,…)\)若存在，选\(x_0 > max(x)\)则\((x_0,x_1,…)\)为\(G’\)的解。故不考虑\(x_0\)时\(G’\)与\(G\)的解集相等。

下面继续给出关于差分约束与差分约束图的定理：

1) 若\(x=(x_1,x_2,…)\)为差分约束\(Ax \leq b\)的解，则\(x+d=(x_1+d,x_2+d,…)\)也是该差分约束的解；

证明：差分约束\(Ax \leq b\)的所有不等式左边都是\(x_n – x_m = (x_n + d) – (x_m + d)\)。

2) 设\(G\)表示差分约束\(Ax \leq b\)，\(x=(\delta(v_0,v_1),\delta(v_0,v_2),…)\)。若\(G\)不含负权环路则\(x\)为可行解；

证明：对于任意边\((v_i,v_j)\)，根据三角不等式有\(\delta(v_0,v_j)-\delta(v_0,v_i) \leq w(v_i,v_j)\)。

3) 设\(G\)表示差分约束\(Ax \leq b\)。若\(G\)含负权环路，则无可行解；

证明：设负权环路\(p=[v_1,v_2,…,v_i]\)，其中\(v_1=v_i\)，把\(p\)的权重计为\(c<0\)。\(p\)上的所有边表示一组约束不等式\(x_{k+1} – x_k \leq w(v_k,v_{k+1})\)，两边求和有\(0 = x_i – x_1 =\sum x_{k+1} – x_k \leq \sum w(v_k,v_{k+1})=c\)，导致矛盾。

最后给出Bellman-Ford解差分约束可行解的流程：

1) 把差分约束转化为额外增加\(v_0\)顶点的约束图；

2) 把约束图的\(v_0\)作为源点执行Bellman-Ford算法；

3) 若约束图中存在负权重环路，则算法必然会侦测到并退出；

4) 若无负权重环路，则\((v_1.d,v_2.d,…)\)可作为原差分约束的一个可行解；

定义约束图时额外添加顶点\(v_0\)的原因在步骤(3)得到体现。因为Bellman-Ford算法只能判断从源点到目标点间是否存在负权环路，并未说明其可判断图是否存在负权环路。由于\(v_0\)到达所有顶点，所以只要图中存在负权环路，那么一定存在目标顶点\(u\)，使\(v_0\)到\(u\)的路径中存在该负权环路。且\(v_0\)将保证对于解\(x=(x_1,x_2…)\)不存在\(x_i = \infty\)。