有向图与无向图
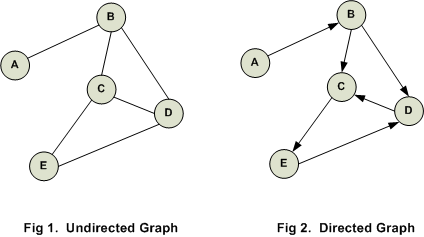
数据结构中的图(Graph)是对数学分支图论(Graph Theory)中的图的表示,通常用二元组\(G=(V,E)\)定义图\(G\),其中\(V\)是顶点的集合(顶点集),\(E\)是边的集合(边集)。边集的元素也是二元组\((x,y)\)且\(x,y\)是\(V\)的元素,由于二元组包含\(x,y\)的序,若不关心\(x,y\)的序或用集合\(\{x,y\}\)表示边,则\(G\)是无向图,否则是有向图。一般按上图的方式“画”有向图和无向图。
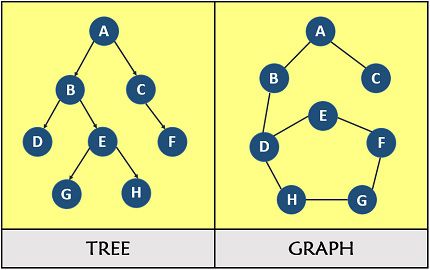
直观上图是对前面讨论过的树的推广,树不允许树边任意的加在两节点间,图边则没有这些限制,并且图中一般不会指定“树根”这样的顶点。所以图相比树会有更多更复杂的“边界情况”,给出与之相关的概念:
1) 重边:即重复的边。设\(u,v\)是图顶点,对于有向图,若存在2个以上的从\(u\)到\(v\)的边,则称从\(u\)到\(v\)有重边。对于无向图,若存在2个以上连接\(u\)和\(v\)的边,则称\(u\)与\(v\)间有重边。也就是边集中有“相同”的二元组;
2) 自环:即连向自己的边。设\(u\)是图顶点,对于有向图或无向图,若存在边\((u,u)\),则称该边是自环。自环还能重复;
3) 路径:设\(u,v\)是图顶点,对于有向图或无向图,若通过1个由边组成的序列可达\(v\),该序列就是\(u\)到\(v\)的其中1个路径,对于有向图这些边的“方向”必须是正确的。如果路径中的每个顶点都仅到达一次,则该路径为简单路径;
4) 环:起点和终点是同一顶点的路径,也称为圈、回路、环路。自环也是环的一种;
5) 度:对于无向图,顶点的度数是其所在的边的总数目,注意自环要当成2个边计数。对于有向图,则没有度但有出度和入度,前者指顶点发出的边数,后者指到达顶点的边数,注意自环会让出度和入度都+1;
对于所有涉及到图结构和图算法的文章,默认图是不允许出现重边和自环的。
图的表示与实现
图结构是较复杂的,但图的形式化定义是二元组,借用形式化定义可得到较简洁的物理实现:
1) 邻接矩阵:对于含N个顶点的图,可构造N*N矩阵A进行描述。由于有向图任意两顶点间至多有2条边,故对于有向图可用\(A_{ij}\)表示顶点i连向顶点j的边,\(A_{ij}\)的值刚好可表示权重(无权时用1/0表示有边/无边)。在处理无向图时通常用\(A_{ij}=A_{ji}\)的方式记录无向边。
2) 邻接表:邻接表是图的更一般化的表示方案,邻接表的KEY代表一个顶点,KEY对应的VALUE为记录这个顶点的所有邻接顶点。比如对于有向图的邻接表\(L\),\(L[u]=[a,b,c]\)表示\(u\)顶点发出3条边分别指向\(a,b,c\)。对于无向图通常的处理方法是如果\(a\)在\(L[u]\)中那么就让\(u\)在\(L[a]\)中。对于有权图可通过继续嵌套表来实现,比如\(L[u][v] = 3\)的形式。
当图的顶点数远远大于边数时,如果使用邻接矩阵存储图的话会有大量空白,但使用邻接表不会有这种问题。所以图表示方案的选择常与图本身的特性有关系。用python字典模拟邻接表如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | """ Graph: addVertex(idx) 增加唯一标识为idx的顶点 addEdge(i1,i2,w) 在i1=>i2间加权重w的边 getWeight(i1,i2) 获得i1,i2间的边 getVertices(i) 获得i的所有邻接顶点 getEdges(i) 获得i的所有出边 vertices 获得图中所有顶点 edges 获得图中所有边 """ class Graph: def __init__(self): self.d = dict() def addVertex(self,i): self.d[i] = dict() def addEdge(self,i1,i2,w): self.d[i1][i2] = w def getWeight(self,i1,i2): return self.d[i1][i2] def getEdges(self,i): return self.d[i] def getVertices(self,i): return self.d[i].keys() def vertices(self): return self.d.keys() def edges(self): return self.d |
图的遍历
图的遍历有广度优先遍历与深度优先遍历两种策略,这两种策略与树的层次遍历和中序遍历十分的类似。最大的区别是遍历图时要用集合记录当前已到达的所有顶点,然后用该集合避免多次访问同个顶点。图的遍历和树的遍历还有一个区别是,树的遍历是从树根开始的,树上的所有节点都是可达的。而图没有根,所以遍历可从任何节点开始,并且不一定所有顶点都可达。
下面会给出“简化版”的广度优先遍历与深度优先遍历的算法,这个算法中的图是基于上述物理结构的。这两个简化版的算法的目标是从任意指定顶点\(x\)出发,按广度优先/深度优先这样的次序,“到达”且仅“到达”一次\(x\)的所有可达顶点。这里之所以用“简化版”这个称呼是因为在之后的文章中还要讨论“通用版”的广度优先搜索(BFS)和深度优先搜索(DFS),通用版的BFS/DFS是很多其他图算法的框架,其远不止是一个“访问且仅访问一次所有顶点”的算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 | def bfs(graph,vertex): visited = [vertex,] queue = [vertex,] while queue: vertex = queue.pop(0) for v in graph.getVertices(vertex): if v not in visited: queue.append(v) visited.append(v) print visited |
1 2 3 4 5 6 7 8 9 10 | def _dfs(graph,vertex,visited): for v in graph.getVertices(vertex): if v not in visited: visited.append(v) _dfs(graph,v,visited) return visited def dfs(graph,vertex): visited = _dfs(graph,vertex,[vertex,]) print(visited) |
简单分析算法的正确性,对于广度优先遍历而言,把“出队某顶点,扫描其全部邻接顶点,记录全部未访问顶点并入队这些顶点”这个过程称作一次“子遍历”。假设从\(u\)开始的广度优先遍历未到达\(v\),但从\(u\)可达\(v\)。那么说明在任何子遍历中都没有到达过\(v\),也就是任何连向\(v\)的边都没有访问过,那么说明所有有边连向\(v\)的顶点都没有发生过子遍历…这样一层层的反推,因为\(u\)有路径连向\(v\)最后会推得\(u\)没有发生过子遍历,导致矛盾。对于深度优先遍历而言,把“从某顶点开始执行子递归”当成一次“子遍历”。假设从\(u\)开始的深度优先遍历未到达\(v\),但从\(u\)可达\(v\),那说明任何“子遍历”都没有到达\(v\),那么在所有有边连向\(v\)的顶点的子遍历在开始前\(v\)都未被到达,开始后\(v\)也未被到达,这就只可能是所有有边连向\(v\)的顶点都未被到达…这样一层层的反推也会得到\(u\)未发生过子遍历的矛盾。
简单分析算法代价,上面分析了所有可达顶点都会到达,然后\(visited\)保证这些顶点只到达一次(只发生一次“子遍历”),无论广度优先还是深度优先,每个顶点\(u\)的“子遍历”一定会去访问这个顶点的发出边。所有可达顶点的所有发出边的上界是\(|E|\),所以总代价一定不超过\(O(|V|+|E|)\),总之代价是线性的。