摊还分析与动态表

摊还分析(Amortized Analysis)

通常算法分析的“目标问题”都是给定1个规模为\(n\)的数据结构和1个算法，分析该算法关于\(n\)的代价并表示为\(O(f(n))\)。如果在此基础上继续分析“在该数据结构连续执行\(k\)次该算法”的问题，用乘法可得\(O(kf(N))\)，其中\(N\)是\(k\)次中最大的\(n\)。由于\(O\)是上界所以该结论完全正确，但可能不够“精确”(离确界不够近)。因为没考虑到每次算法执行后，数据结构本身的变化。如果考虑到，则可能得到小于\(O(kf(N))\)的界，并且其更能反映出该场景下的真实代价。

举例说明上述观点，假设有个“包含\(popAll\)运算”的栈，其除了能\(O(1)\)完成\(push,pop,top\)，还支持\(popAll\)运算，其实现是“循环\(pop\)直到栈顶为空”，如果\(popAll\)执行前栈中有\(n\)个元素，\(popAll\)的代价就是\(O(n)\)。然后带入场景“这个栈是某算法的一部分，该算法会多次调用这个栈的\(push,pop,popAll\)，由于这个算法很复杂，不能确定每次都调用什么运算，也不能确定每次调用前栈的元素数。只知道算法开始时栈是空的”。由于不知道元素数，\(popAll\)的\(O(n)\)代价就不精确了，但我们很想衡量这个栈在该算法中的性能表现，所以构造下面这个需要做算法分析的“目标问题”：

设\(s\)是空栈，\(L=[push(x_1),push(x_2),pop(),popAll()…]\)是关于该栈的运算序列，这里不确定各运算在\(L\)有几次，只保证每次运算合法(不\(pop\)空栈等)，设\(L\)的长度为\(n\)，问按顺序执行完\(L\)的总代价是多少。分别用2种思路分析：

1) 序列长度是\(n\)，所以\(push\)次数最多是\(O(n)\)，栈开始时空的，节点数最多有\(O(n)\)个，所以所有\(pop,popAll\)的\(pop\)加起来至多\(O(n)\)次，由于\(push,pop\)都是\(O(1)\)的，故总代价是\(O(n)\)，平摊到每个操作上的代价是\(\frac{O(n)}{n} = O(1)\)；

2) 栈开始是空的，\(popAll\)所\(pop\)的节点一定能具体对应到前面已经执行过的某几个\(push\)，可想象把\(popAll\)每次\(pop\)的代价分别“记”在其对应的\(push\)上面，做“平摊”处理，“平摊”完后\(popAll\)剩下的代价就是\(O(1)\)，而\(push\)的代价翻倍也还是\(O(1)\)，所以总代价是\(O(n)\)。平摊到每个操作上的代价是\(\frac{O(n)}{n} = O(1)\)；

上述基于运算序列的分析法叫摊还分析(平摊、均摊分析)。把平摊到每个操作的代价称为摊还代价或摊还时间复杂度。比如上面得到\(O(1)\)摊还代价，这个摊还代价是关于“空栈的\(push,pop,popAll\)”操作的，为严谨应说明“对于空栈的\(push,pop,popAll\)序列，任意操作的摊还代价是\(O(1)\)”。当然也可直接用“\(n\)次操作的总代价是\(O(n)\)”描述。

这里要注意，摊还代价必须显式写明是“摊还代价”或“摊还时间复杂度”，不能写做“代价”和“时间复杂度”，因为摊还分析不是一般时间复杂度分析的“技巧”，其定义和普通时间复杂度不同，不做区分会有歧义。直观上\(popAll\)的代价“有时是\(O(1)\)、有时是\(O(n)\)”，只有把这些运算全部结合起来看才能反应本质，所以说其是“平均代价”也不合适。摊还分析由著名美国科学家Tarjan发明和推广，他甚至反过来基于摊还分析本身设计了许多优秀的数据结构与算法。

 

摊还分析策略

实际的摊还分析可能很复杂，甚至有很多数学推导，为此人们总结了3类更具体的摊还分析策略：

1) 聚合分析：这是Tarjan最先提出和使用的策略，其就是上述第1种直接求和求平均的方法，是种“直接分析法”，其流程是构造由不同运算组合而成的\(n\)元素序列，然后找到关于\(n\)的代价\(T(n)\)，最后求平均得出摊还代价\(\frac{T(n)}{n}\)；

2) 核算/记账法：这种策略有点类似上述第2种方法，其核心是假设运算能“存钱”，所有运算会消耗和其代价数目一样的“钱”，哪些运算能存钱、能存多少钱是分析算法的人设计好的，最后算法结束时要保证“余额”非负，于是存钱总额就能作为代价上界，求平均可得摊还代价上界。以上面问题为例，规定每次\(push\)存2块，其自己执行时消耗1块，实际存1块，而\(pop,popAll\)会消耗存的钱，由于任何时刻总\(pop\)次数小于等于总\(push\)次数，所以任何时刻余额非负。那么设实际\(push\)次数是\(m\)，存钱总额就是\(2m\)，这是一个代价上界，由于\(m \leq n\)所以\(2m = O(n)\)是确界，摊还代价是\(O(1)\)。当然如果让\(push\)存“更多钱”也可以，但找到的上界可能离确界太远。除非算法复杂难找确界，否则还是应该找确界；

3) 势能法：核算/记账法的推广，通过类似物理学的“势能”代替“钱”。分析时要设计关于数据结构\(D\)的势函数\(\Phi(D)\)。这里把操作序列\(L\)中的\(L[i]\)的实际代价计为\(c_i\)，执行\(L\)直到刚执行完\(L[i]\)后的\(D\)计为\(D_i\)，定义\(c’_i = c_i + \Phi(D_i) – \Phi(D_{i-1})\)。如果保证\(\Phi(D_0)=0, \Phi \geq 0\)，那\(\sum_{i=0}^{n} c’_i = \sum_{i=0}^{n} c_i + \Phi(D_n) – \Phi(D_0) \geq \sum_{i=0}^{n} c_i\)就是个上界。在不需要确界、或数学上存在困难，可继续构造函数\(f(i) \geq c’_i\)找上界。用势能法分析栈操作可定义\(\Phi(D)\)为栈\(D\)元素数，\(c’_i = c_i + \Phi(D_i) – \Phi(D_{i-1})\)，三种操作\(push,pop,popAll\)的\(c’\)分别是2,0,0。无论如何都有\(\sum_{i=0}^{n} c’_i = O(n)\)；

摊还分析尤其势能法的数学处理较多，会遇到“渐进记号式”，比如遇到相减的“\(O(f(n)) – O(f(n))\)”，由于\(O\)表示确界或上界，所以\(O(f(n)) – O(f(n)) = O(f(n))\)肯定正确。因为不知道这两个\(O(f(n))\)的函数形式，所以不知道它们哪个实际是确界或者两个都不是，无法贸然得出\(O(f(n)) – O(f(n)) = O(1)\)。这种相减的情况在势能法里经常出现，因为在每次操作后，想要用\(\Delta\Phi\)去平摊实际代价，这时\(\Delta\Phi\)可能就带负号。考虑到势函数\(\Phi\)一般是自己构造的，所以一般是知道确界的，如遇到这种情况\(c’_i = c_i + \Delta\Phi = O(f(n)) + (-\Theta(f(n)))\)，根据上界和确界记号的定义，可以假想找个新的势函数\(\Phi’ = A\Phi\)，其中\(A\)是超大常数，大到足以确定\(c_i + \Delta\Phi’ = O(f(n)) + (-\Theta(Af(n))) = O(1)\)。所以一般在遇到\(O(f(n)) – \Theta(f(n))\)时，如果符合这些分析的话，可以直接认为这是等于\(O(1)\)的。

 

摊还分析示例

\(A\)为\(k\)位数组，所有元素为0或1，表示二进制数，对应的十进制数为\(\sum_{i=0}^{k-1} 2^iA[i] \)。让\(A\)递增的算法是从低向高位遍历，若当前位是0就变1且算法退出，是1就变0继续遍历。当每个元素都是1的话，最后会都变成0，等于模拟二进制溢出。按一般的时间复杂度分析方法，1次递增的代价最坏是\(O(k)\)，所以\(n\)次递增的代价是\(O(nk)\)。需要注意到每次递增的代价和该次递增变化的总位数同阶。下面按上述的3种策略分析\(A\)从全0开始，递增\(n\)次的总代价，即递增运算的摊还代价：

1) 聚合分析：核心思路是单独分析每个位的变化次数，第1次递增只有第1位变化，第2次第1、2位变化，第3次第1位变化，第4次第1、2、3位变化……即第\(m\)位每\(2^{m-1}\)次递增变化1次，当\(n\)远大于\(2^{k-1}\)时可认为第\(m\)位每1次递增变化\(2^{-(m-1)}\)次，对每个位求和，共有\(\sum_{i=0}^{k-1} 2^{-i}\)个位变化，根据等比级数求和公式，\(k\)不是无穷大时该式小于1，这个结论也不奇怪，因为前面用了“分数次”这种不存在的概念。总之可得出总代价是\(O(n)\)，摊还代价是\(O(1)\)；

2) 核算/记账法：规定任意位发生“0变1”都存2块钱，“1变0”不存钱，而“0变1”和“1变0”的实际代价都是1。根据算法流程，每次递增至多只有1位发生“0变1”。然后来看任意次递增后的余额，初始时所有位是0，余额也是0，“1变0”是减少余额的，但每次“1变0”都意味着上次发生了“0变1”，所以余额永远非负。这直接说明任意次递增后总的“1变0”次数不会超过总的“0变1”次数，\(n\)次递增至多有\(n\)次“1变0”、\(n\)次“0变1”。所以总代价是\(O(n)\)，摊还代价是\(O(1)\)；

3.1) 势能法：设\(\Phi_i\)为第\(i\)次递增后1的数目，其满足\(\Phi_0=0,\Phi\geq 0\)。然后设\(t_i\)等于第\(i\)次递增中“1变0”的位数，由于每次递增至多只有1位发生“0变1”。所以第\(i\)次递增的实际代价\(c_i \leq t_i+1\)。下面分情况的分析\(\Phi\)：

3.2) 若\(\Phi_{i+1} = 0\)：说明第\(i+1\)次递增导致溢出，第\(i\)次递增后所有位就都是1，即\(\Phi_i = k = t_{i+1}\);

3.3) 若\(\Phi_{i+1} > 0\)：根据算法流程\(\Phi_{i+1} = \Phi_i – t_{i+1} + 1\)；

3.4) 综上\(\Phi_{i+1} \leq \Phi_i – t_{i+1} + 1\)。整理得\(c’_i = c_i + \Phi_i – \Phi_{i-1}\leq 2\)，对\(c’_i\)求和得总代价上界\(O(n)\)；

 

动态表(Dynamic Table)

 

\(
\Phi_i = \begin{cases}
2n_i – s_i ~~(\alpha_i \geq \frac{1}{2})\\ \\
\frac{1}{2}s_i – n_i ~~(\alpha_i < \frac{1}{2})\\ \end{cases}\)

 

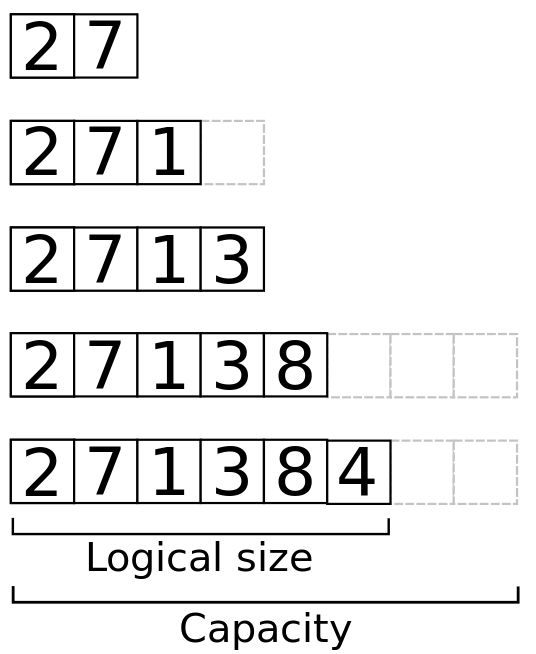
数组在创建时即确定容量上限，创建时不限容量不现实，因为内存是“稀缺”的，而且容量用完时想在数组后继续追加连续内存也不现实，因为后面的内存可能已被占用。所以这时一般的方法是创建更大的数组，再把原来的元素移过去，这将产生\(O(n)\)的代价。相应的如果当前数组很大但元素数很少，为节约连续内存，可创建更小的数组并移动元素。

上述方案看起来简单，但如果在数组插入删除的过程中选择合适的时机做“扩容”和“收缩”，那么“扩容”和“收缩”带来的代价能完全被插入删除平摊。实现了“扩容”和“收缩”的数组称为动态数组，这种策略易推广到基于数组的其他结构，所以把使用这种策略的结构统称动态表。下面给出一种具体的动态数组策略，定义装载因子\(\alpha = \frac{已用容量}{总容量} \)以方便讨论。

1) 初始化：暂时不创建普通数组。规定此时\(\alpha = 1\)；

2) 插入操作：如果当前\(\alpha=1\)(数组已满)，则需“扩容”，创建当前数组长度2倍的普通数组(当前没有数组时创建容量1的数组)，把元素移至该数组并代替旧数组。最后调用普通数组的插入操作；

3) 删除操作：如果当前\(\alpha \leq \frac{1}{4}\)，则需“收缩”，创建当前数组长度0.5倍的普通数组，把元素移至该数组并代替旧数组。最后调用普通数组的删除操作(如果删除后没有其他元素直接删掉数组)；

4) 查找/替换操作：直接使用当前的普通数组上的查找/替换操作；

注意删除操作有一步是“创建当前数组长度0.5倍的普通数组”，这步其实不会得到“非整数”的长度，普通数组长度实际只能取\([0,2^0,2^1,2^2,…]\)。另外“扩容”和“收缩”时机是不对称的有些不合直觉，这是为避免一种最坏情况发生。假如以“\(\alpha \leq \frac{1}{2}\)时收缩”为策略，数组装满时连续执行“插入、删除、插入、删除……”，就会连续发生“扩容、收缩、扩容、……”。设这时元素数为\(n\)，每次动态数组操作就有“扩容”或“收缩”的\(O(n)\)额外代价。之前讨论过，普通数组操作的最好最坏代价分别是\(O(1)\)和\(O(n)\)，如果普通数组发生\(O(n)\)代价的操作，\(O(n)\)的额外代价没影响，但如果是\(O(1)\)代价的操作，\(O(n)\)的额外代价会使动态数组操作的整体代价变成\(O(n)\)，且摊还代价不会更低，因为“扩容、收缩”可以一直持续下去。直观上看来\(a=\frac{1}{2}\)和\(a=\frac{1}{4}\)间的“空隙”是为了平摊掉这种最坏代价，这留出了约“元素数的\(\frac{1}{4}\)”个\(O(1)\)操作，用来将额外的\(O(n)\)代价平摊到\(O(1)\)。

由于是借动态数组讨论动态表，所以并不关心普通数组的操作代价，关心的是“扩容收缩”的\(O(n)\)额外代价能否平摊到\(O(1)\)，为方便可认为普通数组操作都是\(O(1)\)的，然后就方便用上面的势函数摊还分析，其中\(n\)为当前元素数，\(s\)为当前普通数组的容量，下标\(i\)表示第\(i\)个操作刚结束的状态。初始\(\alpha = 1\)故\(\Phi_0=0\)，其他情况\(\Phi\)非负。假设从空动态数组执行操作，此时刚执行完第\(i\)个操作，把\(\Phi_i – \Phi_{i-1}\)计作\(\Delta\Phi_i\)。当不发生“扩张”和“收缩”，根据操作前后\(\alpha\)的范围和插入删除分情况讨论可得\(c_i = O(1)\)和\(\Delta\Phi_i = \pm O(1)\)。当不发生“扩张”和“收缩”，分情况讨论可得\(c_i = O(n_i)\)和\(\Delta\Phi_i = -\Theta(n_i)\)。综合起来\(c_i + \Delta\Phi_i = O(1)\)为常数，即每个操作的摊还代价。\(O(n_i) – \Theta(n_i) = O(1)\)是因为可假想让\(\Phi\)乘超大常数后作为新的势函数。

下面具体实现上述动态数组策略，Python没提供原生数组，其提供的list底层也使用动态数组策略，所以list实现动态数组等于“动态数组套动态数组”，这里用1个变量作每次创建的“数组”的“容量”，用这个变量判断是否需要扩张收缩。