二叉树的高度
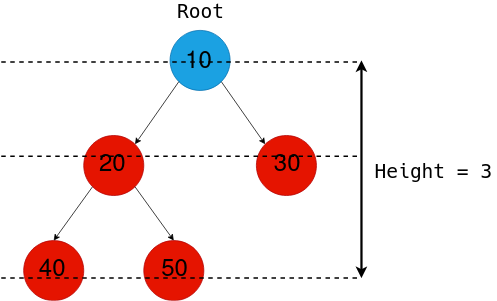
如上图所示,可直观的把二叉树节点分层,也可以递归定义节点所在的层(Level)为“树根在第1层,其他节点的层数等于其父亲节点的层数加1”。树中层数最大的节点的层数称为树的深度(高度)。层数满足如下性质:
a1) 二叉树在第\(k\)层的最大节点数为\(2^{k-1}\);
a2) 设二叉树的节点数为\(n\),深度为\(m\),则\(n\leq 2^m – 1\);
有些教材会从0开始计层(level)或将单节点二叉树的高度计为0,所以之后文章里的高度可能和这里不同。
二叉树的形态
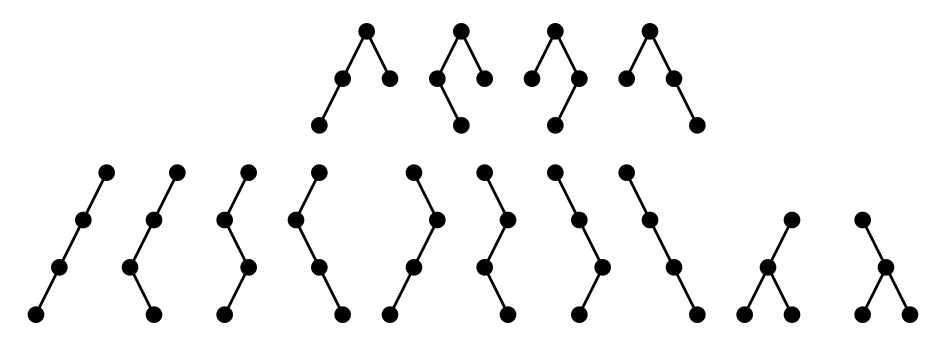
直观上如果两个二叉树画出来后“重合”就称它们相似或形态相同,考虑将这种直观概念转化成严格定义,先用\(S(T_1,T_2)\)表示二叉树\(T_1,T_2\)是否相似,直观上如果两个二叉树的树根、左子树、右子树都分别“重合”,那么两个二叉树“重合”,基于这点可严格给出\(S(T_1,T_2)\)的递归定义为“若\(T_1,T_2\)的树根都为空则返回真,若\(T_1,T_2\)的树根只有1个为空则返回假,若\(T_1,T_2\)的树根都非空则返回\(S(L_1,L_2)\)且\(S(R_1,R_2)\)。其中\(L_1,L_2\)分别是\(T_1,T_2\)的左子树,\(R_1,R_2\)分别是\(T_1,T_2\)的右子树”。
然后根据上述定义考虑\(n\geq 0\)个节点能组成多少种两两互不相似的二叉树,即多少种二叉树形态,这里将其计为\(F(n)\),不妨认为\(F(0)=1\)。这个问题的关键是如何“划分”所有形态,由于左子树节点数不同的二叉树一定不相似,所以可按左子树的节点数为\(0,1,…,n-1\)将所有形态分\(n\)类,当左子树有\(i\)个节点时左子树本身有\(F(i)\)种形态,相应的右子树有\(n-i-1\)个节点,所以有\(F(n-i-1)\)种形态,根据形态的性质可知当左子树有\(i\)个节点时二叉树有\(F(i)F(n-i-1)\)种形态。那么对上面的\(n\)种分类求和可得到递推式\(F(n)=\sum_{i=0}^{n-1} F(i)F(n-1-i)\),该式刚好是第\(n\)个卡特兰数(Catalan Number)的递推定义,借助卡特兰数的通项公式可知\(F(n)=\frac{C_{2n}^n}{n+1}\),其渐进形式为\(O(\frac{4^n}{n^{1.5}})\)。卡特兰数跟很多算法有关,在组合数学领域十分重要。
上文不用“相同”来表示“相似”是因为默认不同节点之间是可区分的,换句话说若将同一组节点组合2次得到2个二叉树\(T_1,T_2\),只有\(T_1,T_2\)相似且各位置上的节点完全一样才能称\(T_1,T_2\)相同。下面整理出关于相似和相同的性质:
b1) \(n\geq 0\)个节点能构成\(C(n)\)种互不相似的二叉树;
b2) \(n\geq 0\)个节点能构成\(n!\cdot C(n)\)种互不相同的二叉树;
二叉树节点的度
图论中有度(degree)的概念,而树节点的度与之有一定区别,其定义为“若节点\(node\)发出\(k\)条边,则称节点\(node\)的度等于\(k\)”,叶子节点的度等于0。二叉树节点的度只能取0,1,2。度也能反映树的形态,二叉树的度满足如下性质,为方便讨论将二叉树中度等于0,1,2的节点总数分别计为\(n_0,n_1,n_2\):
c1) 二叉树的总节点数\(n=n_0+n_1+n_2\);
c2) 二叉树的总边数等于\(n-1=n_1+2n_2\);
c3) 二叉树满足\(n_0=n_2+1\);
证明:利用c1,c2可得。
二叉树子树间的关系
有时会关心二叉树任意两节点对应的子树间的关系,比如这2个子树是有公共节点等,下面给出相关性质:
d1) 设\(a\neq b\)是同个二叉树的节点,\(a,b\)为对方的祖先或子孙 <=> \(a,b\)的最近公共祖先(LCA)等于\(a\)或\(b\);
d2) 设\(a\neq b\)是同个二叉树的节点,\(a,b\)为对方的祖先或子孙 <=> \(a,b\)子树有公共节点;
d3) 设\(a\neq b\)是同个二叉树的节点,\(a\)的兄弟子树与\(b\)的兄弟子树一定无公共节点;
完美二叉树与完全二叉树
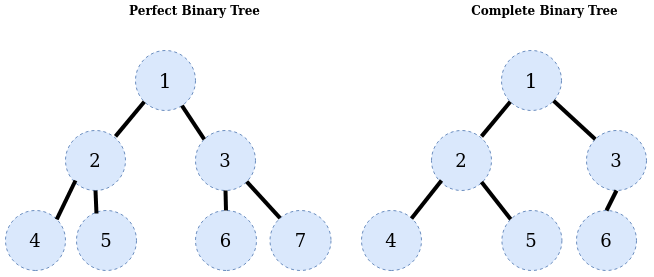
上文讨论了二叉树形态,这里讨论两类具体形态,讨论前先约定一种二叉树的节点编号规则,具体可参考上图,即先从上到下,然后从左到右的在节点上标记1,2,3……。下面基于该编号规则给出这两类二叉树形态的定义:
1) 完美二叉树(Perfect Binary Tree):高度为\(h\geq 0\)的二叉树\(T\)是完美二叉树当且仅当\(T\)的节点数为\(2^h-1\);
2) 完全二叉树(Complete Binary Tree):高度为\(h\geq 0\)的二叉树\(T\)是完全二叉树当且仅当\(T\)满足如下条件:
2.1) 若\(h\leq 1\):\(T\)是完美二叉树;
2.2) 若\(h>1\):\(T\)的第1层到第\(h-1\)层必须能构成完美二叉树,且对于第\(h-1\)层中的任意节点,若其有左孩子,则所有编号小于它的同层节点都有2个孩子,若其有右孩子,则其必须也有左孩子。所以完美二叉树是完全二叉树的子集;
上图是这两类形态的例子,直观上来说完美二叉树刚好能将每层的空位都占满,完全二叉树只保证将第1层到倒数第2层的空位都占满,并且倒数第1层的节点是从左到右依次填入空位的。对于每个高度,都对应唯一的完美二叉树形态。对于每个节点数,都对应唯一的完全二叉树形态,但可能没有对应的完美二叉树形态。由于不是任意数量的节点都能构成完美二叉树,所以其应用场景不如完全二叉树广泛。下面给出完全二叉树的一些重要性质:
e1) 对于由\(n\)个节点组成的完全二叉树,其高度等于\(\lfloor\log_2n\rfloor + 1\),其中\(\lfloor \rfloor\)表示向下取整;
证明:设该树的高度为\(m \geq 2\),那么高度为\(m – 1, m\)的完美二叉树的节点数分别等于\(2^{m-1} – 1, 2^m – 1\)。由于该树也可能是完美二叉树故\(2^{m-1} – 1 < n \leq 2^m – 1\),由于不等式3边都是整数故\(2^{m-1} \leq n < 2^m\)即\(m-1\leq \log_2n < m\)。注意到\(m\)和\(m-1\)是整数,向下取整后\(m-1 = \lfloor\log_2n\rfloor\),即\(m = \lfloor\log_2n\rfloor + 1\),证毕(\(m=1\)时易直接验证)。
e2) 完全二叉树是节点数相同时高度最小的形态之一;
e3) 设完全二叉树的节点数为\(n\),则节点编号有如下关系:
e3.1) 编号\(i\)的节点有左孩子的充要条件是\(n\geq 2i\)。左孩子存在时其编号是\(2i\);
e3.2) 编号\(i\)的节点有右孩子的充要条件是\(n\geq 2i+1\)。右孩子存在时其编号是\(2i+1\);
e3.3) 设节点编号为\(j\),若\(j=1\)则其是树根(无父亲节点),若\(j>1\)则其父亲节点编号是\(\lfloor\frac{j}{2}\rfloor\);
证明:设完全二叉树\(T\)的高度和节点数分别为\(m,n\)(\(m\geq 2\)),根据上述完全二叉树的定义,\(T\)的第1到\(m-1\)层可看作完美二叉树,故\(T\)第\(m-1\)层的节点数是\(2^{m-2}\),尾节点编号是\(2^{m-1}-1\)、首节点\((2^{m-1}-1)-(2^{m-2})+1=2^{m-2}\)。第\(m-1\)层内部的第\(i\)个节点(\(i\)始于0)的编号是\(x=2^{m – 2}+i\),其前面有\(L=i\)个节点,后面有\(R=2^{m-2}-i-1\)个节点。编号\(x\)的节点若有左孩子,根据定义编号小于\(x\)的节点都有2个孩子,所以编号为\(x\)的节点的左孩子的编号只能取\(x+R+2L=2x\),所以左孩子存在时节点数必须满足\(n\geq 2x\),这就是(1)的充要性和左孩子编号。根据定义可立即用(1)证明(2)。最后用前2者证明(3),对于任何完全二叉树,节点按编号都依次是“树根、左孩子、右孩子、左孩子、右孩子、……”,即编号\(j>1\)为奇数表示右孩子,为偶数表示左孩子。当\(j>1\)为偶数时\(\lfloor\frac{j}{2}\rfloor = \frac{j}{2}\geq 1\),\(2\lfloor\frac{j}{2}\rfloor = j\)。为奇数时\(\lfloor\frac{j}{2}\rfloor = \frac{j-1}{2}\geq 1\),\(2\lfloor\frac{j}{2}\rfloor+1 = j\)。根据(1)和(2)无论\(j>1\)是奇数还是偶数,\(\lfloor\frac{j}{2}\rfloor\)编号的节点总会是\(j\)编号的节点的父亲节点。
上述性质(e3)表明对于由\(n\)个节点组成的完全二叉树和由\(n\)个元素组成的数组,可根据上述的节点编号规则建立二叉树节点与数组元素(索引)的一一对应关系,于是就能用数组来表示完全二叉树,这是一种常用的完全二叉树表示法。