左偏树与左偏堆

空节点路径长度(Null Path Length)

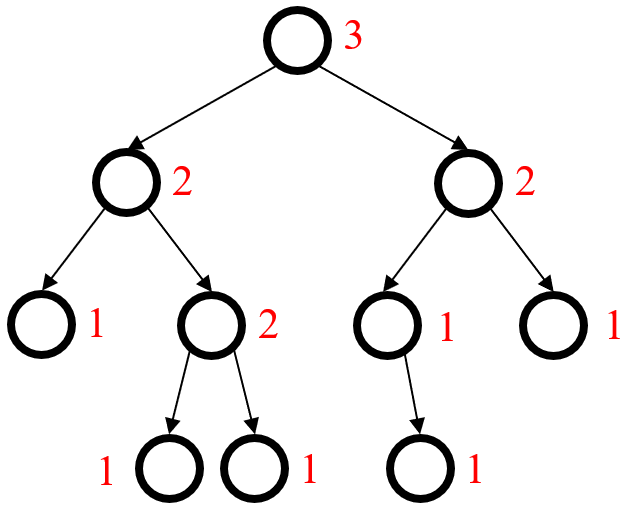
定义二叉树节点\(x\)的空节点路径长度\(npl(x)\)等于从\(x\)到\(x\)子树中的空节点的最小距离。于是若\(x\)为空节点则\(npl(x)=0\)，否则若\(x\)有空孩子则\(npl(x)=1\)，否则\(npl(x)>1\)。需明确大部分教材规定\(npl\)始于-1。下面给出与之相关的重要性质：

a1) 设\(x\)为二叉树中的非空节点，则\(x\)子树的前\(npl(x)\)层是完美二叉树，前\(npl(x)+1\)层不是完美二叉树；

证明：\(npl(x)=1\)时该命题易验证，只需考虑\(npl(x)>1\)的情况。首先\(x\)子树前\(npl(x)-1\)层的节点都必须有2个非空的孩子，否则会导致\(npl(x)\)小于当前值的矛盾，于是其前\(npl(x)\)层必然能被看作高度为\(npl(x)\)的完美二叉树。但在第\(npl(x)\)层必然存在有至少1个空孩子的节点，否则将导致\(npl(x)\)大于当前值的矛盾，于是其前\(npl(x)+1\)层不能被看作完美二叉树。

a2) 设\(x\)为二叉树中的非空节点，则\(x\)子树的节点数\(n_x \geq 2^{npl(x)}-1\)；

证明：根据(a1)，\(x\)子树的前\(npl(x)\)层是完美二叉树，这部分有\(2^{npl(x)}-1\)个节点，而去掉其他层的节点不影响\(npl(x)\)；

a3) 设\(x\)为二叉树中的非空节点，则\(npl(x) \leq \lfloor \log_2{(n_x+1)} \rfloor\)，其中\(n_x\)是\(x\)子树的节点数；

根据之前文章对完全二叉树的讨论，对于包含\(n>0\)个节点的任意二叉树，其树根\(r\)的高度不小于\(\lfloor\log_2n\rfloor + 1\)，而结合上述性质可知\(npl(r)\)不超过\(\lfloor\log_2n\rfloor + 1\)，这说明可以尝试构造\(O(npl(r))\)代价的算法来实现更高的性能。

左偏树(Leftist Tree)

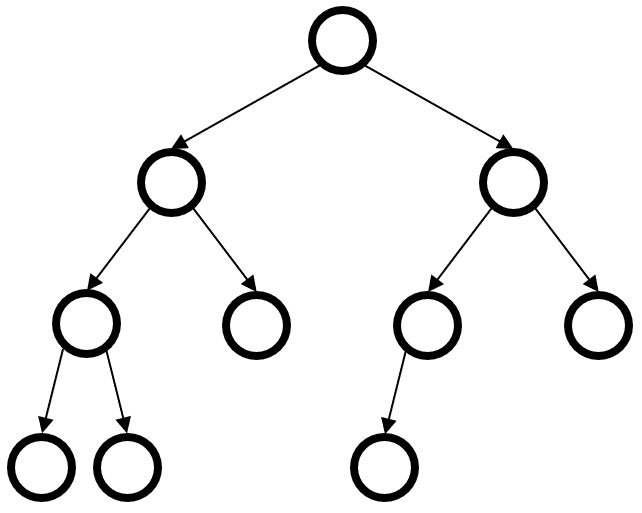
在确定好空节点路径长度的概念后，可直接递归的定义左偏树为空二叉树或树根\(r\)满足\(npl(r.left) \geq npl(r.right)\)且左右子树都是左偏树的二叉树。上图是左偏树的例子。接下来给出一个左偏树最主要的性质：

b1) 设\(x\)为左偏树中的非空节点，则\(x\)子树的右链表的节点数等于\(npl(x)\)；

证明：根据(a1)右链表节点数不小于\(npl(x)\)，若大于\(npl(x)\)则右链表中必存在\(x\)使\(npl(x.left) < npl(x.right)\)导致矛盾。

左偏树相比普通二叉树只是提供了右链表这个确定的空节点路径，所以在左偏树上更有可能构造出\(O(npl(r))\)代价的算法，其中\(r\)为左偏树的树根。对普通二叉树的树根执行\(f(r)\)即可使其成为左偏树，递归操作\(f(r)\)的步骤如下：

1) 若\(r\)为空：直接返回0；

2) 若\(r\)非空：置\(l=f(r.left),r=f(r.right)\)。若\(l<r\)则交换左右指针的指向然后返回\(1+l\)，否则返回\(1+r\)；

上述步骤的正确性很容易验证，\(f(r)\)每次返回的都是\(npl(r)\)，而交换节点\(r\)的左右子树不影响\(npl(r)\)的值本身。

左偏堆(Leftist Heap)

1971年左右美国学者Clark A. Crane提出左偏堆，这是种基于左偏树的堆。由于花费较低代价即可合并2个左偏堆，所以左偏堆属于可并堆(mergeable heap)。一个左偏堆首先是一个左偏树，其节点除了要存储关键字\(key\)，还需额外存储\(npl\)值，因为在左偏堆的运算中需要获取节点的\(npl\)，而实时计算\(npl\)的代价是无法接受的。左偏堆需要实现的运算如下：

1) \(merge(r_1, r_2)\)：将以\(r_1,r_2\)为树根的2个左偏堆合并成1个左偏堆，然后再返回该左偏堆的树根；

2) \(get()\)：从左偏堆中去掉其中一个最小关键字并返回它；

3) \(put(k)\)：在左偏堆中插入一个等于\(k\)的关键字；

需明确上述\(get,put\)结束时须保证符合左偏堆的定义。下面给出上述运算的步骤，其中\(merge\)运算的步骤可参考上图，图左侧的部分自顶向下的表示递归的下降过程，右侧的部分则自底向上的表示递归的回溯过程：

1) \(merge(r_1, r_2)\)：具体步骤分情况如下：

1.1) \(r_1,r_2\)不都非空：若\(r_1\)为空则返回\(r_2\)，否则返回\(r_1\)；

1.2) \(r_1,r_2\)都非空且\(r_1.key \leq r_2.key\)：置\(r_1.right=merge(r_1.right, r_2)\)。若\(r_1.left\)非空则置\(a=r_1.left.npl\)，否则置\(a=0\)。置\(b=r_1.right.npl\)。若\(b>a\)则交换\(r_1\)的左右孩子，置\(r_1.npl=a+1\)，否则置\(r_1.npl=b+1\)。返回\(r_1\)；

1.3) \(r_1,r_2\)都非空且\(r_1.key>r_2.key\)：置\(r_2.right=merge(r_2.right, r_1)\)。若\(r_2.left\)非空则置\(a=r_2.left.npl\)，否则置\(a=0\)。置\(b=r_2.right.npl\)。若\(b>a\)则交换\(r_2\)的左右孩子，置\(r_2.npl=a+1\)，否则置\(r_2.npl=b+1\)。返回\(r_2\)；

2) \(get()\)：若树根为空则抛异常。否则计树根为\(r\)，置\(k=r.key\)，然后置新树根为\(merge(r.left, r.right)\)，最后返回\(k\)；

3) \(put(k)\)：创建新节点\(x\)并置\(x.key=k\)，计树根为\(r\)，然后置新树根为\(merge(r, x)\)；

上述运算都以\(merge\)为基础，由于单个节点是左偏堆，左偏堆中的节点(子树)也都是左偏堆，所以只要能证明\(merge\)正确则其他运算就正确。首先如果\(r_1,r_2\)不都非空则\(merge\)显然能正确执行，所以只需要验证\(r_1,r_2\)都非空的情形即可。不妨先直接要求上述的步骤(1.2)在“置\(r_1.right=merge(r_1.right, r_2)\)”后就直接返回\(r_1\)，步骤(1.3)在“置\(r_2.right=merge(r_2.right, r_1)\)”后就直接返回\(r_2\)，那么如果\(r_1,r_2\)不都是空节点，\(merge(r_1,r_2)\)在进入子递归前就已确定最终要返回的节点和该节点的左子树，并且它们一定是\(merge(r_1,r_2)\)刚执行时的\(r_1,r_1.left\)或\(r_2,r_2.left\)，整个过程的最后一次子递归\(merge(r’_1,r’_2)\)会因为\(r’_1,r’_2\)不都非空而直接返回，若将整个过程在步骤(1.2)或(1.3)返回的节点计为\(x_1…x_n\)，则对于\(merge(r_1,r_2)\)返回的二叉树，仅\(x_1…x_n\)的\(npl\)值可能不正确，仅\(x_1…x_n\)可能不符合\(npl(x.left) \geq npl(x.right)\)的左偏树性质。所以步骤(1.2)或(1.3)在子递归结束后的回溯阶段需要解决该问题，而这只需在回溯阶段判断是否交换左右孩子，并更新即将返回的节点的\(npl\)值即可。

由于\(merge(r_1,r_2)\)包含的递归次数不超过其执行前\(r_1\)与\(r_2\)中的右链表长度之和，故其代价为\(O(npl(r_1)+npl(r_2))\)。于是对于树根为\(r\)的左偏堆，\(get\)的代价为\(O((npl(r)-1)+(npl(r)-1))\)，\(put\)的代价为\(O(npl(r))\)。它们都是对数形式的。

总结与实现

注意到上述步骤(1.2)和(1.3)是完全对称的，如果将步骤(1.3)替换成“返回\(merge(r_2, r_1)\)”，则其完全与原来的步骤(1.3)等价。而之所以在一开始这样定义步骤(1.2)和(1.3)，只是为了方便描述对算法步骤的分析。下面给出左偏堆的程序实现。