链表相关问题 – JONY'S WORDPRESS

反转链表

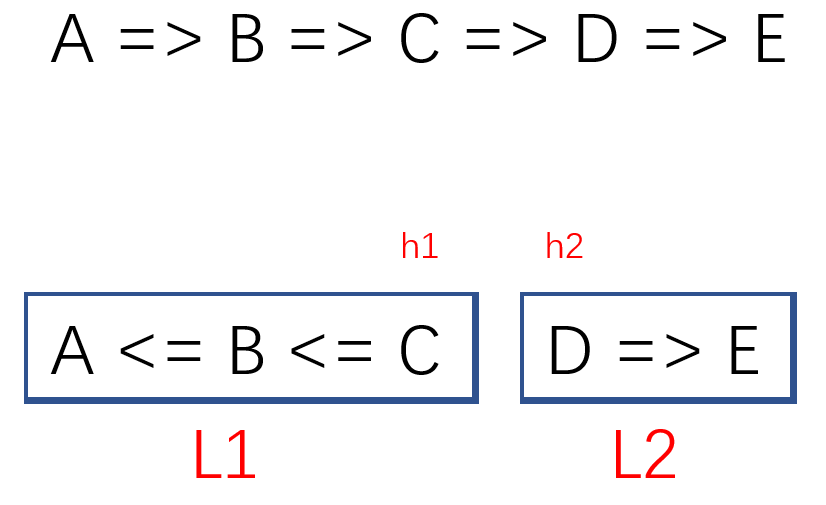
该问题是“给定链表(表头节点)，将链表逆序，要求原地完成(由原节点构成)且只占常数额外空间”。先考虑递归程序，思路是递归进入到链表尾，然后在每次递归退出时，让外层递归把当前节点原后继的 $next$ 反过来指向当前节点。需注意最后一次递归结束后，其当前节点的 $next$ 没有发生变化，所以要特别的将其指向空，那为了方便干脆在每轮递归结束前都加一步把当前节点的 $next$ 指向空。然后是如何记录新表头，上述递归没有用到函数返回值，可以一层层返回新表头。

def f(node):
    if not node.next:
        return node
    newHead = f(node.next)
    node.next.next = node
    node.next = None
    return newHead

def f(node):

if not node.next:

return node

newHead = f(node.next)

node.next.next = node

node.next = None

return newHead

然后考虑只遍历一次的非递归程序，如上图所示，先把链表分为“已反转子链表 $L_1$ ”和“未反转子链表 $L_2$ ”，并要求每次迭代后， $L_1,L_2$ 的每个节点的 $next$ 都符合已反转子链表、未反转子链表的意义的。表示 $L_1,L_2$ 表头的变量 $h_1,h_2$ 在每次迭代后都是符合定义的。迭代开始前 $h_1$ 为空， $h2_2$ 为原链表表头。然后执行如下迭代步骤：

1) 建立临时变量 $tmp$ 指向 $h_2.next$ 。 $tmp$ 即将作为新 $h_2$ ；

2) 将 $h_2.next$ 指向 $h_1$ 。 $h_2$ 即将作为新 $h_1$ ；

3) 把 $h_1$ 指向 $h_2$ ，再把 $h_2$ 指向 $tmp$ 。当前迭代的工作已做完，这步是为下轮迭代提供正确的 $h_1,h_2$ ；

4) 当前 $h_2$ 为空则程序结束，当前 $h_1$ 就是新的表头，否则继续返回(1)迭代；

def f(head):
    h1 = None
    h2 = head
    while True:
        tmp = h2.next
        h2.next = h1
        h1, h2 = h2, tmp
        if not tmp:
            return h1

def f(head):

h1 = None

h2 = head

while True:

tmp = h2.next

h2.next = h1

h1, h2 = h2, tmp

if not tmp:

return h1

逆序存储链表

该问题是“给定链表(表头)，将其按遍历逆序存入数组”。该问题很简单，如果用递归遍历，就不用反转链表或数组。

def f(head):

    result = []

    def r(head):
        if head:
            r(head.next)
            result.append(head)
    r(head)

    return result

def f(head):

result = []

def r(head):

if head:

r(head.next)

result.append(head)

r(head)

return result

按大小划分链表

该问题是“给定链表和 $x$ ，使所有小于 $x$ 的节点在不小于 $x$ 的节点前，且两部分链表节点各保持原有顺序，要求原地完成(由原节点构成)且只占常数额外空间”。这个问题就是稳定的快速排序算法在每次迭代时要解决的问题。这里的思路是想办法按小于 $x$ 和大于等于 $x$ 分割成2个链表，再把两个链表接起来。具体就是先遍历原链表 $L_1$ ，遇到小于 $x$ 的元素不操作，遇到大于等于 $x$ 的元素就将其从 $L_1$ 取下接到 $L_2$ 尾部。遍历结束后再将 $L_1$ 表尾指向 $L_2$ 表头即可。

这个问题的逻辑本身简单，但用程序实现时要考虑的边界比较多，这也是链表类问题的特点。比如删 $L_1$ 元素的迭代过程要记录待删除节点的前驱才能实现，且还要考虑到表头被删的情况。对于 $L_2$ 则要记得把最终表尾的 $next$ 指向空，且还要考虑到初始时 $L_2$ 是空的。为了处理这些情况，可以在原表头前加一个自己创建的节点作为新表头，最后记得还原回去即可。这样的好处是“删除表头”、“表头为空”等情况好处理，都可借助自己创建的节点的 $next$ 完成。

def f(head, x):

    h1 = n1 = ListNode(0)
    h2 = n2 = ListNode(0)
    h1.next = head

    while n1.next:
        if n1.next.val < x:
            n1 = n1.next
        else:
            n2.next = n1.next
            n1.next = n1.next.next
            n2 = n2.next
            n2.next = None
            
    n1.next = h2.next
    return h1.next

def f(head, x):

h1 = n1 = ListNode(0)

h2 = n2 = ListNode(0)

h1.next = head

while n1.next:

if n1.next.val < x:

n1 = n1.next

else:

n2.next = n1.next

n1.next = n1.next.next

n2 = n2.next

n2.next = None

n1.next = h2.next

return h1.next

合并排序链表

该问题是“给定 $A,B$ 两个升序链表(表头)，将其合并为一个，要求原地完成(用原来的节点)且只占常数的额外空间”。先创建存储结果的空链表 $L$ ，使用上面提到的技巧，先自己创建一个节点作为其表头。然后跟合并排序数组的思路一样，每轮比较 $A,B$ 最左端两个数，取下其中最小的节点追加到 $L$ 尾部，直到有一个链表为空，把另一个链表追加到 $L$ 的尾部即可。最后 $L$ 的表头(自己创建的节点的后继节点)就是结果链表的表头。具体实现如下。

def f(l1, l2):

    h = ListNode(0)
    hh = h

    while l1 and l2:
        if l1.val < l2.val:
            h.next = l1
            l1 = l1.next
        else:
            h.next = l2
            l2 = l2.next
        h = h.next
        h.next = None
    
    if not l2:
        h.next = l1
        return hh.next
    
    if not l1:
        h.next = l2
        return hh.next

def f(l1, l2):

h = ListNode(0)

hh = h

while l1 and l2:

if l1.val < l2.val:

h.next = l1

l1 = l1.next

else:

h.next = l2

l2 = l2.next

h = h.next

h.next = None

if not l2:

h.next = l1

return hh.next

if not l1:

h.next = l2

return hh.next

链表加法

该问题是“给定 $A,B$ 链表(表头)，两个链表分别表示两个整数，其中链表元素是0~9的1位十进制数，链表元素的次序表示从低位到高位，比如3=>2=>1表示123。要求输出同样格式的链表能表示上述两数之和”。这个问题的关键点是进位以及进位导致的边界情况的处理，由于每次的位相加最大只能得到9+9+进位=19，所以只需一个额外变量描述上次是否进位即可。当 $A,B$ 都遍历完时，仍有可能还有1个之前的进位，需要为其再创建一个节点。

def f(h1, h2):
    hh = h = ListNode(None)
    flg = False
    while flg or h1 or h2:
        v = 1 if flg else 0
        if h1:
            v += h1.val
            h1 = h1.next
        if h2:
            v += h2.val
            h2 = h2.next
        if v >= 10:
            v -= 10
            flg = True
        else:
            flg = False
        h.next = ListNode(v)
        h = h.next
    return hh.next

def f(h1, h2):

hh = h = ListNode(None)

flg = False

while flg or h1 or h2:

v = 1 if flg else 0

if h1:

v += h1.val

h1 = h1.next

if h2:

v += h2.val

h2 = h2.next

if v >= 10:

v -= 10

flg = True

else:

flg = False

h.next = ListNode(v)

h = h.next

return hh.next

两两交换链表节点

该问题是“给定链表(表头)，从左到右两两交换节点位置，剩一个元素时无需交换。比如1-2-3-4-5变为2-1-4-3-5”。这个问题的关键是区分边界，因为表头会改变，所以这里先创建一个节点 $N$ ，把原表头接到其后面。想要实现交换2个节点的位置，那这2个节点必须要能表示成“后继”和“后继的后继”。这里给出具体迭代步骤：

1) 初始化 $h = N$ ；

2) 若 $h.next$ 或 $h.next.next$ 不存在，则 $h$ 之后的部分无需再交换，程序结束返回 $N.next$ ；

3) 交换 $h.next, h.next.next$ 的位置并维护相关指针的正确性；

4) $h = h.next.next$ 然后返回步骤(2)；

上述步骤中每一轮都是利用 $x$ 来交换 $x.next,x.next.next$ ，一轮结束后 $x$ 前进两步，就又能交换后面另外两个节点，当某一轮的 $x$ 发现后不到2个节点时，就说明无需继续交换，程序退出。

def f(head):
    hh = h = ListNode(None)
    h.next = head
    while h.next and h.next.next:
        tmp = h.next
        h.next = tmp.next
        tmp.next = h.next.next
        h.next.next = tmp
        h = h.next.next
    return hh.next

def f(head):

hh = h = ListNode(None)

h.next = head

while h.next and h.next.next:

tmp = h.next

h.next = tmp.next

tmp.next = h.next.next

h.next.next = tmp

h = h.next.next

return hh.next

奇偶链表

该问题是“给定链表(表头)，其节点是从1开始编号的，整理链表使奇数编号节点都在偶数编号节点前，并维持原顺序。要求原地完成(用原来的节点)并只占常数额外空间，比如输入a-b-c-d-e输出a-c-e-b-d”。这个问题的解决框架和上述“两两交换链表节点”类似，每次迭代都以“当前节点、当前节点后继、当前节点后继的后继”3个为一组操作，每次都把奇数节点取下接入“奇数链表”，最后当前链表会是“偶数链表”，合并两链表即可。程序实现如下，这里还是用创建表头的技巧处理边界。

def f(head):
    h1 = hh1 = ListNode(None)
    h2 = hh2 = ListNode(None)
    h1.next = head
    while h1.next:
        tmp = h1.next
        h1.next = h1.next.next
        if h1.next:
            h1 = h1.next
        h2.next = tmp
        h2 = h2.next
        h2.next = None
    h2.next = hh1.next
    return hh2.next

def f(head):

h1 = hh1 = ListNode(None)

h2 = hh2 = ListNode(None)

h1.next = head

while h1.next:

tmp = h1.next

h1.next = h1.next.next

if h1.next:

h1 = h1.next

h2.next = tmp

h2 = h2.next

h2.next = None

h2.next = hh1.next

return hh2.next

倒数第 $n$ 个链表节点

该问题是“给定链表(表头)，求其倒数第 $n$ 个节点(从1开始计数)”。这个问题容易想到的方法是先遍历一次求出节点数，换算出其正序编号，然后遍历第二次找到这个节点。这里看一种只遍历一次的方法，首先设两个变量 $x,y$ 指向表头，然后开始迭代，每次迭代结束做 $x = x.next$ 。当第 $n$ 次迭代结束时后，之后每次迭代结束还要额外做 $y = y.next$ 。最终当 $x$ 到达表尾程序结束时， $y$ 指向的就是倒数第 $n$ 个节点。由于用了2个变量(指针)，所以这种方法也叫“双指针法”。具体实现如下。

def f(node, n):
    i = 0
    x = y = node
    while x:
        i += 1
        x = x.next
        if i > n:
            y = y.next
    return y

def f(node, n):

i = 0

x = y = node

while x:

i += 1

x = x.next

if i > n:

y = y.next

return y

排序链表的中位数

该问题是“给定升序排序的链表(表头)，求其中位数节点，当节点数为偶数，则返回中间两个节点靠左的”。这里使用另一种基于2个指针的策略，称为“快慢指针法”。同样是先用两个变量 $x,y$ 指向表头，然后开始迭代，每轮 $x$ 前进1个节点， $y$ 前进2个节点。当 $y$ 到达链表尾时， $x$ 就停在中位数节点上。实现时要处理好 $y$ 前进2次导致的边界情况，具体步骤如下：

1) 初始时 $x,y$ 都指向表头；

2) $y$ 前进一步，如果失败( $y.next$ 指向空)则程序结束返回 $x$ ；

3) $y$ 前进一步，如果失败( $y.next$ 指向空)则程序结束返回 $x$ ；

4) $x$ 前进一步，然后回到(2)。如果能到达这一步，那这一步不可能失败；

只要链表有至少1个节点，该步骤就能找到题意的节点。节点数为奇数时程序在(2)结束，偶数时在(3)结束。

def f(node):
    x = y = node
    while True:
        if not y.next:
            return x
        y = y.next
        if not y.next:
            return x
        y = y.next
        x = x.next

def f(node):

x = y = node

while True:

if not y.next:

return x

y = y.next

if not y.next:

return x

y = y.next

x = x.next

判断链表环

该问题是“给定链表(表头)，其允许节点的 $next$ 指向比其遍历序更前的节点，这时会形成环路，请判断该链表是否有环”。容易想到的方法是遍历时用额外数组记录已访问节点，每次遍历都去这个数组中检查，其代价是 $O(n^2)$ 并占用 $O(n)$ 的额外空间，这其实就是深度优先搜索。这里用“快慢指针法”实现更优的程序，先看上面“排序链表的中位数”程序，如果某轮迭代退出则直接说明链表无环，有环的话迭代永远不会结束。如果一轮迭代没退出，那么 $y$ 前进2次， $x$ 前进1次，所以当有环时，无论环多大，一定在某轮迭代结束时 $x,y$ 指向相同元素，那么在每轮迭代结束时加一步检查 $x,y$ ，相同则判定有环并返回。

简单讨论下时间复杂度，首先可以确定 $x$ 在环上至多绕一圈，因为 $x$ 如果在环上， $y$ 必然也在环上，如果 $x$ 绕了一圈程序还未退出，那么 $y$ 就绕了2圈， $y$ 一定会在某个节点与 $x$ 相遇。这说明 $x$ 至多走 $O(n)$ 步，程序整体代价为 $O(n)$ 。

def f(node):
    x = y = node
    while True:
        if not y.next:
            return False
        y = y.next
        if not y.next:
            return False
        y = y.next
        x = x.next
        if x is y:
            return True

def f(node):

x = y = node

while True:

if not y.next:

return False

y = y.next

if not y.next:

return False

y = y.next

x = x.next

if x is y:

return True

链表环的入口

该问题是“给定链表(表头)，判断其是否有环并找到环入口(顺序遍历时最先到达的环节点)”。这里以上面的“判断链表环”的程序为基础来讨论，设从表头出发走 $s\geq 0$ 步能到环入口，从环入口出发走 $k\geq 1$ 步能到其自身(也是环节点数)。

为讨论 $s$ 与 $k$ 的倍数的关系，将 $s$ 表示为 $s = nk + m$ ， $0\leq m<k$ 与 $n\geq 0$ 为整数。当 $x$ 走到环入口时 $y$ 多走 $nk+m$ 步， $y$ 的当前位置可看作其从环入口出发走了 $m$ 步，此时 $y$ 继续走 $k-m$ 步可达 $x$ ，但在程序里 $y$ 是跟着 $x$ 走的，那就让 $x$ 走 $k-m$ 步， $y$ 会多走 $k-m$ 步刚好能追上 $x$ 相遇，这说明从相遇点出发走 $m$ 步可到达环入口，根据 $s = nk + m$ ，这意味着相遇后，从相遇点和表头出发2个指针，每次都只走1步，经过 $nk + m$ 步两指针会在环入口相遇。由于 $nk + m$ 是未知的，在程序中两个指针每走一次就互相看一下是否相等即可。具体程序如下，这里直接使用一部分上面的函数。

def meetAt(node):
    x = y = node
    while True:
        if not y.next:
            return False
        y = y.next
        if not y.next:
            return False
        y = y.next
        x = x.next
        if x is y:
            return x

def f(head):
    node = meetAt(head)
    if node:
        while head != node:
            head = head.next
            node = node.next
        return head

def meetAt(node):

x = y = node

while True:

if not y.next:

return False

y = y.next

if not y.next:

return False

y = y.next

x = x.next

if x is y:

return x

def f(head):

node = meetAt(head)

if node:

while head != node:

head = head.next

node = node.next

return head

发表评论 取消回复

发表评论取消回复