AOV网与拓扑排序
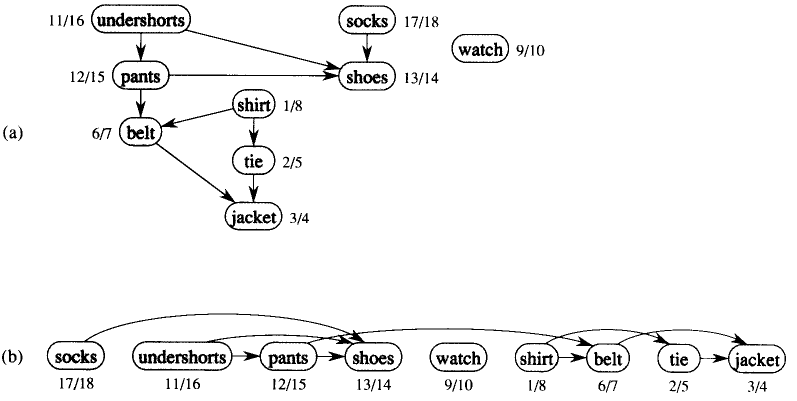
日常生活中常需要流程化的完成有依赖关系的事(比如“穿鞋前必须穿裤,穿鞋前必须穿袜”)。这类关系适合用有向无环图描述,其中的顶点表示任务,边表示任务之间的依赖关系。这个图之所以“无环”是因为如果存在环会导致任务“循环依赖”,导致环路上的任务无法找到可行的执行次序,即有环时这个图就没有意义。这样的描述任务依赖的有向无环图一般称为AOV网,在AOV网执行拓扑排序的结果是得到由AOV网所有顶点组成的序列,按该序列的次序执行任务不会违反依赖关系。
下面给出拓扑排序的定义“有向无环图上的拓扑排序(Topological Sorting)是将图的所有顶点排成有序序列,对于序列中的任意两顶点,若存在u到v的路径则v必然排在u之后”。
class AOV:
def __init__(self):
self.d = dict()
def addVertex(self,i):
self.d[i] = set()
def delVertex(self,i):
self.d.pop(i)
def addEdge(self,i1,i2):
self.d[i1].add(i2)
def getVertices(self,i):
return self.d[i]
@property
def vertices(self):
return self.d.keys()
@property
def edges(self):
return self.d
基于入度的算法(Kahn算法)
“在每轮把图中0入度顶点(包括其出边)都删除,删除顺序就是该图的某个拓扑序列”。讨论其正确性:
1) 在任意轮“剩下”的图都是原图的子图,若该子图非空又无0入度顶点则有环,即原图有环;
2) 设u先于v被删除且有v到u的路径,那在v被删除前v和v的出边都不变(或失去意义),该“关系”会沿v出边“传递”到后继顶点。所以不删v则从v到u的路径不会改变,u的入度无法为0,所以不存在从v到u的路径;
\(O(|V|+|E|)\)时间复杂度的实现如下,其每轮删除所有0入度顶点的同时找到了下轮所有0入度顶点:
1) 求该图所有顶点的“入度表”,再求出“当前0入度顶点队列”;
2) 从队列取顶点从图中删除并把其全部邻接顶点入度-1,若有顶点入度减为0那么将其加入队列;
3) 循环上述步骤直到队列为空,如果最后图不为空集说明该图有环;
def topSort(aov):
inDegrees = dict((v,0) for v in aov.vertices)
zeroInDegrees = []
result = []
for e in aov.vertices:
for v in aov.getVertices(e):
inDegrees[v] += 1
for v,i in inDegrees.items():
if i == 0:
zeroInDegrees.append(v)
while zeroInDegrees:
v = zeroInDegrees.pop(0)
for v2 in aov.getVertices(v):
inDegrees[v2] -= 1
if inDegrees[v2] == 0:
zeroInDegrees.append(v2)
aov.delVertex(v)
result.append(v)
print(result)
print(aov.edges)
基于DFS的算法
“从任意顶点DFS,把所有顶点按‘变黑时间’降序排列就是某个拓扑序列”。讨论其正确性:
1) 首先给出DFS下的判环方法“该图无环\({<=>}\)该图执行任意DFS得到的森林都无后向边”。对必要性证明如下,设图中有环C然后从图中执行任意一种DFS,在某时刻v是C中首个被染灰的顶点,\((u,v)\)为C中的边。此时由白色路径定理可知在某DFS形成的生成树(森林)中u是v的后裔,故\((u,v)\)为后向边。
2) 然后证明“DFS后图中所有边\((u,v)\)满足\(u.t_2>v.t_2\)”。DFS保证仅访问一次所有边,到达边\((u,v)\)时u必为灰色。然后分情况进行讨论。若v为灰色根据边分类算法该图有环(有后向边)。如果v为白色则v马上被染灰执行子DFS,根据括号化结构\(u.t_2>v.t_2\)。若v为黑色则\(v.t_2\)已确定但\(u.t_2\)未确定故\(u.t_2>v.t_2\)。
3) 把顶点按\(t2\)降序排序,从中前后任取两顶点u与v,根据2)可知无法找到v到u的边与路径。
def dfs(aov, vertex, white, black):
for v in aov.getVertices(vertex):
if v in white:
white.remove(v)
dfs(aov, v, white, black)
black.append(vertex)
def topSort(aov):
white = set(aov.vertices)
black = list()
for v in aov.vertices:
if v in white:
white.remove(v)
dfs(aov, v, white, black)
black.reverse()
print(black)